Giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là:
Tập xác định
Ta có:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là:
Tập xác định
Ta có:
Cho hai số thực x, y thỏa mãn ![]() và x + y = 1. Giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
và x + y = 1. Giá trị nhỏ nhất và giá trị lớn nhất của biểu thức ![]() lần lượt là:
lần lượt là:
Ta có:
Đặt t = xy ta được
Vì
Mặt khác
Khi đó bài toán trở thành tìm giá trị lớn nhất của hàm số trên
Xét hàm số xác định và liên tục trên
Ta có:
=> Hàm số g(t) nghịch biến trên đoạn
=>
Tìm các giá trị của tham số m để bất phương trình ![]() nghiệm đúng với mọi
nghiệm đúng với mọi ![]()
Xét hàm số ta có:
=>
Ta có:
Giá trị lớn nhất của hàm số ![]() trên khoảng
trên khoảng ![]()
Ta có:
=> Giá trị lớn nhất của hàm số trên khoảng đã cho bằng 3 khi x = 1
Tìm giá trị thực của tham số m để hàm số f(x) = -x3 – 3x2 + m có giá trị nhỏ nhất trên đoạn [-1; 1] bằng 0.
Xét hàm số f(x) = -x3 – 3x2 + m trên đoạn [-1; 1] ta có:
f’(x) = -3x2 – 6x
f’(x) = 0 =>
Ta tính được
Cho hàm số y = f(x) và có bảng biến thiên trên [-2; 3) như sau:
Giá trị lớn nhất của hàm số trên đoạn [-2; 3] bằng:
Từ đồ thị của hàm số y = f(x) ta thấy hàm số y = f(x) xác định và liên tục trên đoạn [-2; 3]
Ta có: f(x) ∈ [-2; 3] với =>
Trên khoảng (0; +∞) thì hàm số y = -x3 + 3x + 1
Ta có:
Từ bảng biến thiên => Hàm số có giá trị lớn nhất bằng 3
Gọi M và m lần lượt là giá trị lớn nhất và giá tị nhỏ nhất của hàm số ![]() trên tập
trên tập ![]() . Tính giá trị H của m.M
. Tính giá trị H của m.M
Tập xác định của hàm số y là:
Ta có:
Ta có bảng biến thiên như sau:
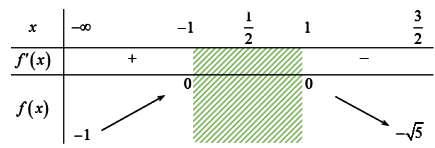
Từ bảng biến thiên ta được:
Tìm giá trị lớn nhất của hàm số ![]() trên khoảng
trên khoảng ![]() bằng:
bằng:
Đặt
Khi đó:
So sánh và
ta thấy GTLN là
Cho hàm số y = f(x) và có bảng biến thiên trên [-5; 7) như sau:
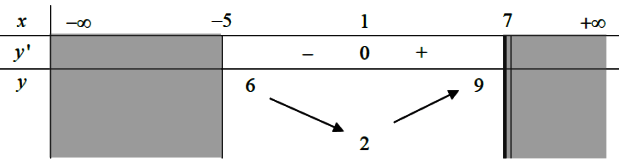
Mệnh đề nào sau đây đúng?
Dựa vào bảng biến thiên dễ dàng ta thấy
là sai vì f(x) sẽ nhận các giá trị 7; 8 lớn hơn 6 khi x tiến tới 7
là sai vì f(x) không bằng 9 mà chỉ tiến đến 9 khi x dần đến 7 (x khác 7)
Vậy chọn đáp án A.
Cho hàm số có bảng biến thiên như hình dưới đây.
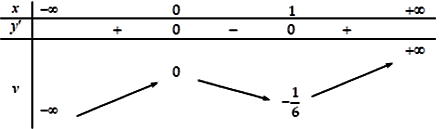
Khẳng định nào sau đây là đúng?
Từ bảng biến thiên ta nhận thấy đạo hàm của hàm số đổi dấu từ dương sang âm qua nghiệm 0 nên hàm số đạt cực đại tại 0 và giá trị cực đại của hàm số bằng 0.
Cho hàm số y = x4 – 2x2 + 5. Khẳng định nào sau đây đúng:
Tập xác định
Ta có bảng biến thiên
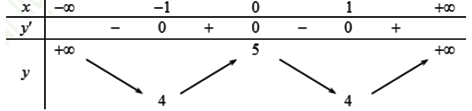
Dựa vào bảng biến thiên ta thấy hàm số có giá trị nhỏ nhất, không có giá trị lớn nhất.
Cho hàm số ![]() (với m là tham số thực). Tìm giá trị lớn nhất của tham số m để hàm số có giá trị nhỏ nhất bằng -2 trên đoạn [0; 3].
(với m là tham số thực). Tìm giá trị lớn nhất của tham số m để hàm số có giá trị nhỏ nhất bằng -2 trên đoạn [0; 3].
Xét hàm số trên đoạn [0; 3] ta có:
=> Hàm số f(x) đồng biến trên (0; 3)
=>
Theo bài ra ta có:
Gọi M là giá trị lớn nhất của hàm số ![]() . Tính tích các nghiệm của phương trình f(x) = M.
. Tính tích các nghiệm của phương trình f(x) = M.
Đặt
Xét hàm số ta có:
Tìm giá trị nhỏ nhất của hàm số ![]() trên khoảng (0; 1)
trên khoảng (0; 1)
Hàm số xác định và liên tục trên (0; 1) ta có:
Lập bảng biến thiên:
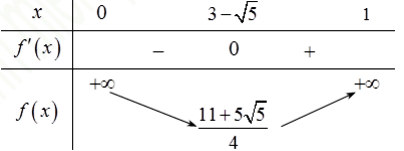
Từ bảng biến thiên ta có:
Gọi S là tập các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số là ![]() trên đoạn [0; 2] không vượt quá 30. Tổng các phần tử của S bằng bao nhiêu?
trên đoạn [0; 2] không vượt quá 30. Tổng các phần tử của S bằng bao nhiêu?
Gọi S là tập các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số là trên đoạn [0; 2] không vượt quá 30. Tổng các phần tử của S bằng bao nhiêu?
Cho hàm số y = f(x) liên tục trên và có bảng biến thiên như hình vẽ.
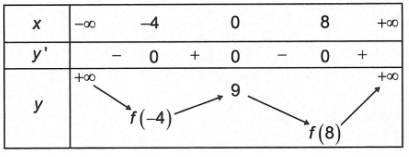
Biết f(-4) > f(8), khi đó giá trị nhỏ nhất của hàm số đã cho trên bằng:
Từ bảng biến thiên ta có:
Mặt khác f(-4) > f(8) => thì
Vậy
Người ta khảo sát gia tốc a(t) của một vật thể chuyển động (t là khoảng thời gian tính bằng giâu từ lúc vật thể chuyển động) từ giây thứ nhất đến giây thứ ba ghi nhận được a(t) là một hàm số liên tục có đồ thị như hình bên:
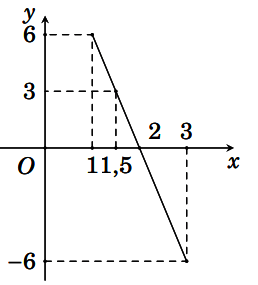
Hỏi trong thời gian từ giây thứ nhất đến giây thứ ba được khảo sát đó, thời điểm nào vận tốc lớn nhất?
Gợi ý: Mối quan hệ giữa gia tốc và vận tốc
Từ đồ thị ta có: a(t) = 0 => v’(t) = 0 = > t = 2
Ta có bảng biến thiên:
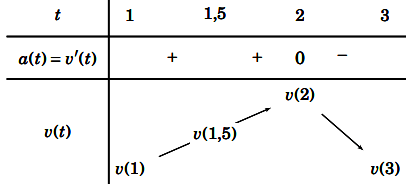
=> Vận tốc lớn nhất đạt được khi t = 2
Tìm giá trị lớn nhất của hàm số ![]() trên đoạn [-6; 6]
trên đoạn [-6; 6]
Xét hàm số g(x) = -x2 – 4x + 5 liên tục trên đoạn [-6; 6]
Ta có: g’(x) = -2x – 4
=> g’(x) = 0 => x = -2 thuộc [-6; 6]
Ta lại có g(x) = 0 => x2 – 4x + 5 = 0 => x = 1 (tm) hoặc x = -5 (tm)
Ta tính được:
Giả sử m là giá trị nhỏ nhất của hàm số ![]() trên khoảng
trên khoảng ![]() . Tính giá trị của m.
. Tính giá trị của m.
Ta có:
Ta có bảng biến thiên như sau:
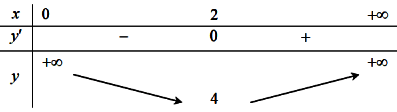
=> Giá trị nhỏ nhất của hàm số bằng 4
=> y(2) = 4
=> m = 4
