Hàm số ![]() đạt cực tiểu tại điểm
đạt cực tiểu tại điểm
Ta có: có tập xác định
=> Hàm số đạt cực tiểu tại điểm x = 1
Hàm số ![]() đạt cực tiểu tại điểm
đạt cực tiểu tại điểm
Ta có: có tập xác định
=> Hàm số đạt cực tiểu tại điểm x = 1
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số ![]() không có cực trị. Số phần tử của S là:
không có cực trị. Số phần tử của S là:
Xét hàm số ta có:
Hàm số đã cho không có cực trị
=> Phương trình y’ = 0 vô nghiệm hoặc có nghiệm kép
=>
Do m là số nguyên nên
Vậy tập S có 4 phần tử.
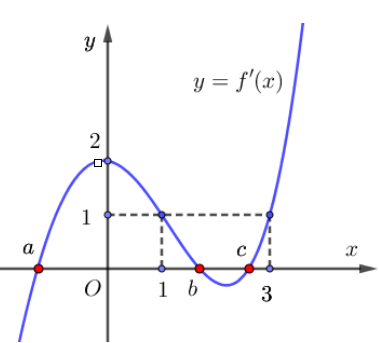
Cho hàm số y = f(x). Biết hàm số y = f’(x) có đồ thị như hình vẽ bên dưới. Số điểm cực trị của hàm số ![]() là:
là:
Ta có:
Do
Vậy hàm số có ba điểm cực trị.
Số điểm cực trị của hàm số ![]() là?
là?
Xét hàm số
Ta có:
Ta có bảng biến thiên:
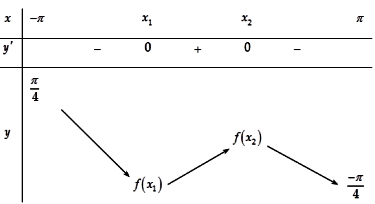
Dựa vào bảng biến thiên, ta thấy hàm số có hai điểm cực trị và đồ thị hàm số cắt trục hoành tại hai điểm phân biệt khác x1; x2
=> Hàm số có 5 điểm cực trị
Cho hàm số y = f(x) có đạo hàm ![]() . Số điểm cực trị của hàm số đã cho bằng
. Số điểm cực trị của hàm số đã cho bằng
Ta có:
=> Hàm số có 3 điểm cực trị
Cho hàm số ![]() . Xét các mệnh đề sau, những những mệnh đề nào đúng?
. Xét các mệnh đề sau, những những mệnh đề nào đúng?
Ta có:
Ta có bảng xét dấu như sau:

Quan sát bảng xét dấu ta thấy:
- Hàm số có 3 điểm cực trị
- Hàm số đồng biến trên khoảng (-1; 0), (1; +∞) và nghịch biến trên khoảng (-∞; -1), (0; 1)
Gọi A, B, C là các điểm cực trị của đồ thị hàm số ![]() . Bán kính của đường tròn nội tiếp tam giác ABC bằng:
. Bán kính của đường tròn nội tiếp tam giác ABC bằng:
Ta có:
=> Đồ thị hàm số có ba điểm cực trị là A(0; 4), B(1; 3), C(-1;; 3)
Tính được
Áp dụng công thức tính bán kính đường tròn nội tiếp tam giác ABC ta có:
Cho hàm số ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Tập xác định
Cho hàm số y = f(x) có đạo hàm ![]() . Hỏi hàm số có bao nhiêu điểm cực trị?
. Hỏi hàm số có bao nhiêu điểm cực trị?
Ta có:
=> Hàm số có 1 cực trị
Cho hàm số f(x) có đạo hàm . Gọi P là giá trị cực đại của hàm số đã cho. Chọn khẳng định đúng.
Ta có:
Ta có bảng biến thiên như sau:
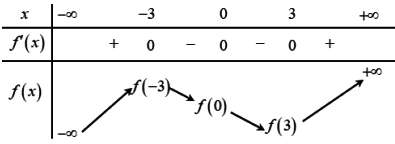
Dựa vào bảng biến thiên ta có giá trị cực đại của hàm số là P = f(-3)
Cho hàm số ![]() có đồ thị (C). Biết rằng đồ thị (C) có ba điểm cực trị tạo thành ba đỉnh của tam giác ABC. Diện tích tam giác ABC bằng:
có đồ thị (C). Biết rằng đồ thị (C) có ba điểm cực trị tạo thành ba đỉnh của tam giác ABC. Diện tích tam giác ABC bằng:
Ta có:
Tọa độ các điểm cực trị của đồ thị hàm số là
=> Tam giác ABC vuông cân tại A =>
Cho hàm số y = f’(x) như hình vẽ. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số ![]() để hàm số
để hàm số ![]() có đúng 11 điểm cực trị?
có đúng 11 điểm cực trị?
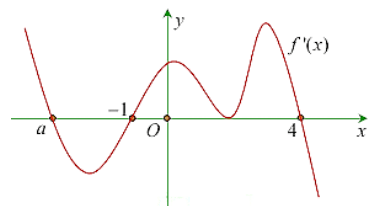
Hàm số đạt cực trị tại
Xét hàm số
Bảng biến thiên của hàm số suy ra chỉ có phương trình
cho ta nghiệm bội lẻ.
Nếu
=> Số điểm cực trị u là 1
=> Số nghiệm bội lẻ của phương trình u = 4 tối đa 2 nghiệm bội lẻ (Không thỏa yêu cầu)
Khi m > 0 => Số điểm cực trị u là 5 ta có bảng biến thiên của hàm số
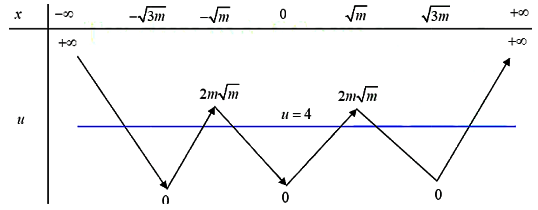
Áp dụng công thức:
Số điểm cực trị của hàm số f(u) = số nghiệm bội lẻ của phương trình (u = 4) + số điểm cực trị của u
=> . Kết hợp với điều kiện
=> Có 29 giá trị nguyên thỏa mãn yêu cầu.
Cho hàm số bậc bốn y = f(x) có đồ thị (C1) và hàm số y = f’(x) có đồ thị (C2) như hình vẽ bên. Số điểm cực trị của đồ thị hàm số ![]() trên khoảng
trên khoảng ![]() là:
là:
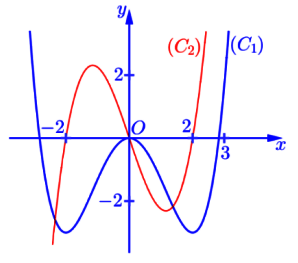
Ta có:
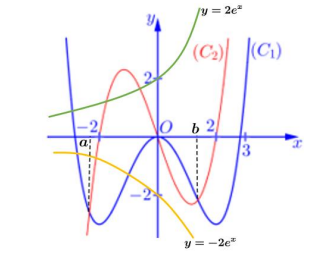
Xét
Từ đồ thị ta được:
Phương trình có nghiệm đơn
Phương trình có 2 nghiệm đơn và 1 nghiệm bội chẵn (x = 0)
Phương trình có 1 nghiệm đơn.
Vậy g’(x) = 0 có 8 nghiệm đơn nên hàm số g(x) có 8 điểm cực trị.
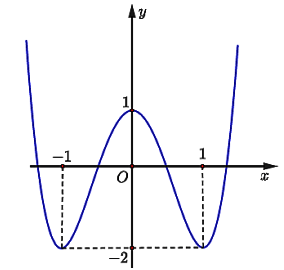
Cho hàm số bậc bốn có đồ thị như hình vẽ dưới đây:

Số điểm cực trị của hàm số ![]() là:
là:
Ta có:
Cho hàm số ![]() . Giả sử hàm số đạt cứ đại tại x = a và đạt cực tiểu tại x = b thì giá trị biểu thức 2a – 5b là
. Giả sử hàm số đạt cứ đại tại x = a và đạt cực tiểu tại x = b thì giá trị biểu thức 2a – 5b là
Tập xác định
Ta có:
Ta có bảng xét dấu như sau:
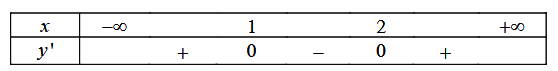
Do y’ thay đổi dấu từ dương sang âm khi đi qua điểm x = 1
=> x = 1 là điểm cực đại của hàm số
y’ đổi dấu từ âm sang dương khi đi qua điểm x = 2
=> x = 2 là điểm cực tiểu của hàm số
=> 2a – 5b = -8
Cho hàm số f(x) liên tục trên ![]() và có bảng biến thiên của đạo hàm như sau:
và có bảng biến thiên của đạo hàm như sau:

Hàm số  có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
Xét hàm số , ta có bảng giá trị |t(x)|
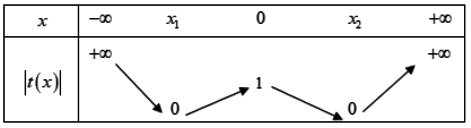
Ta có:
Hàm số không có đạo hàm tại điểm
Tại mọi điểm ta có:
=>
Dựa vào bảng giá trị hàm |t| suy ra:
+ Phương trình (1), (2) vô nghiệm
+ Phương trình (3) có 4 nghiệm phân biệt khác 0
+ Phương trình (4) có hai nghiệm phân biệt khác 0 và khác các nghiệm của phương trình (3)
=> g’(x) = 0 có 7 nghiệm và qua các nghiệm này g’(x) đều đổi dấu
Từ (*) ta thấy g’(x) cũng đổi dấu khi x đi qua 2 điểm
Vậy hàm số g(x) có 9 điểm cực trị.
Hàm số ![]() có cực đại là:
có cực đại là:
Ta có:
=> x = 0 là điểm cực đại của hàm số
Cho hàm số y = f(x) có đạo hàm. Biết f(x) có đạo hàm f’(x) và hàm số y = f’(x) có đồ thị như hình vẽ:

Hàm số g(x) = f(x - 1) đạt cực đại tại điểm nào dưới đây?
Cách 1: Ta có:
Vậy chọn đáp án B
Cách 2: Đồ thị hàm số g’(x) = f’(x – 1) là phép tịnh tiến đồ thị hàm số y = f’(x) theo phương trục hoành sang bên phải 1 đơn vị. Ta có hình vẽ minh họa:
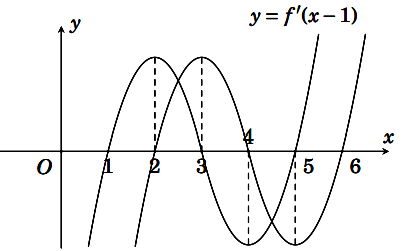
Đồ thị hàm số g’(x) = f’(x – 1) cắt trục hoành tạo các điểm có hoành độ x = 2, x = 4, x = 6 và giá trị hàm số g’(x) đổi dấu từ dương sang âm khi qua điểm x = 4
Chọn B
Hàm số ![]() có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
Tập xác định
Ta có:
Do y’ không đổi dấu nên hàm số không có cực trị.
Gọi S là tập hợp chứa tất cả các giá trị thực của tham số m để hàm số ![]() có điểm cực đại với giá trị cực đại tương ứng nằm trong khoảng (3; 4) và đồng thời thỏa mãn 10m là số nguyên. Số phần tử của tập hợp S là:
có điểm cực đại với giá trị cực đại tương ứng nằm trong khoảng (3; 4) và đồng thời thỏa mãn 10m là số nguyên. Số phần tử của tập hợp S là:
Xét phương trình
Nếu thì hàm số
không có điểm cực đại.
Nếu thì phương trình (*) có hai nghiệm phân biệt là
Với thì
không có điểm cực đại.
Với thì
Hàm số này đạt cực đại tại x = m + 2 và giá trị cực đại là
Vậy điều kiện để hàm số có cực đại là:
Do 10m là số nguyên nên có hai giá trị thỏa mãn là
