Lớp 12 Toán 12

Luyện tập Mặt tròn xoay (Trung bình)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Thể tích của khối nón

    Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn ngoại tiếp của đáy ABC đến một mặt bên là \frac{a}{2}. Thể tích của khối nón ngoại tiếp hình chóp SABC bằng:

    Hướng dẫn:

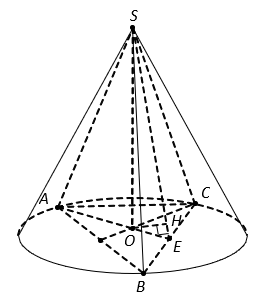
     Thể tích khối nón

    Gọi E là trung điểm của BC, dựng OH \bot SE tại H.

    Chứng minh được OH \bot \left( {SBC} ight) nên suy ra OH = d\left[ {O,\left( {SBC} ight)} ight] = \frac{a}{2}.

    Trong tam giác đều ABC, ta có OE = \frac{1}{3}AE = \frac{1}{3}.\frac{{2a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}

    và  OA = \frac{2}{3}AE = \frac{{2a\sqrt 3 }}{3}

    Trong tam giác vuông SOE, ta có

    \frac{1}{{O{H^2}}} = \frac{1}{{O{E^2}}} + \frac{1}{{S{O^2}}} \Rightarrow \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{E^2}}} = \frac{1}{{{a^2}}} \Rightarrow SO = a.

    Vậy thể tích khối nón V = \frac{1}{3}\pi O{A^2}.SO = \frac{1}{3}\pi {\left( {\frac{{2a\sqrt 3 }}{3}} ight)^2}.a = \frac{{4\pi {a^3}}}{9}  (đvtt).

  • Câu 2: Thông hiểu
    Tính thể tích khối trụ

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chu vi đáy bằng 2a thì thể tích của nó bằng:

    Hướng dẫn:

     Gọi bán kính đáy là R.

    Hình trụ có chu vi đáy bằng 2a nên ta có 2\pi R = 2a \Leftrightarrow R = \frac{a}{\pi }.

    Suy ra hình trụ này có đường cao h=a.

    Vậy thể tích khối trụ V = \pi {R^2}h = \pi {\left( {\frac{a}{\pi }} ight)^2}a = \frac{{{a^3}}}{\pi }(đvtt).

  • Câu 3: Vận dụng cao
    Tính tỉ số thể tích

    Từ một tấm tôn hình chữ nhật kích thước 50{m{cm}} \times 240{m{cm}} , người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50 cm , theo hai cách sau (xem hình minh họa sau đây):

    Tính tỉ số thể tích

    ● Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.

    ● Cách 2. Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.

    Kí hiệu V_1là thể tích của thùng gò được theo cách 1 và V_2 là thể tích của thùng gò được theo cách 2. Khi đó tỉ số \frac{{{V_1}}}{{{V_2}}} bằng:

    2 || Hai || hai

    Đáp án là:

    Từ một tấm tôn hình chữ nhật kích thước 50{m{cm}} \times 240{m{cm}} , người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50 cm , theo hai cách sau (xem hình minh họa sau đây):

    Tính tỉ số thể tích

    ● Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.

    ● Cách 2. Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.

    Kí hiệu V_1là thể tích của thùng gò được theo cách 1 và V_2 là thể tích của thùng gò được theo cách 2. Khi đó tỉ số \frac{{{V_1}}}{{{V_2}}} bằng:

    2 || Hai || hai

     Công thức thể tích khối trụ V = \pi {R^2}h.

    ● Ở cách 1, suy ra h= 50 cm và 2\pi {R_1} = 240 \Leftrightarrow {R_1} = \frac{{120}}{\pi }. Do đó {V_1} = \pi .{\left( {\frac{{120}}{\pi }} ight)^2}.50 (đvtt).

    ● Ở cách 2, suy ra mỗi thùng có h= 50 cm và 2\pi {R_2} = 120 \Leftrightarrow {R_2} = \frac{{60}}{\pi }

    Do đó {V_2} = 2 \times \left[ {\pi .{{\left( {\frac{{60}}{\pi }} ight)}^2}.50} ight] (đvtt).

    Suy ra \frac{{{V_1}}}{{{V_2}}} = 2

  • Câu 4: Nhận biết
    Mệnh đề đúng

    Xét các mệnh đề:

    (I) Tập hợp các đường thẳng d thay đổi nhưng luôn luôn song song và cách đường thẳng \triangle cố định một khoảng không đổi là một mặt trụ.

    (II) Hai điểm A, B cố định. Tập hợp các điểm M trong không gian mà diện tích tam giác MAB không đổi là một mặt trụ.

    Trong các mệnh đề trên, mệnh đề nào đúng?

    Hướng dẫn:

    Ta xét về khái niệm Mặt trụ suy ra  (I) đúng.

    Diện tích tam giác MAB không đổi khi và chỉ khi khoảng cách từ M đến đường thẳng AB không đổi (giả sử bằng R ).

    Vậy tập hợp các điểm M là mặt trụ bán kính R và trục là AB.

    Vì vậy Mệnh đề (II) cũng đúng.

  • Câu 5: Vận dụng
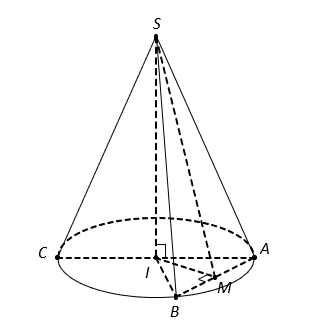
    Diện tích của thiết diện

    Một hình nón có bán kính đáy R, góc ở đỉnh là 60^0. Một thiết diện qua đỉnh nón chắn trên đáy một cung có số đo 90^0 . Diện tích của thiết diện là:

    Hướng dẫn:

     Diện tích của thiết diện

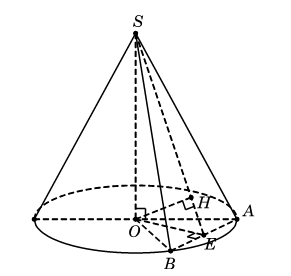
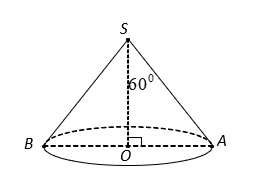
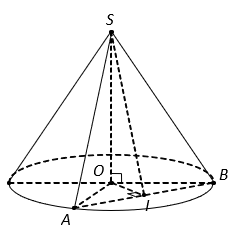
    Vì góc ở đỉnh là 60^0nên thiết diện qua trục SAC là tam giác đều cạnh 2R.

    Suy ra đường cao của hình nón là SI = R\sqrt 3.

    Tam giác SAB là thiết diện qua đỉnh, chắn trên đáy cung AB có số đo bằng 90^0 nên IAB là tam giác vuông cân tại I, suy ra AB = R\sqrt 2.

    Gọi M là trung điểm của AB thì \left\{ \begin{array}{l}IM \bot AB\\SM \bot AB\end{array} ight. và IM = \frac{{R\sqrt 2 }}{2}.

    Trong tam giác vuông SIM, ta có SM = \sqrt {S{I^2} + I{M^2}} = \frac{{R\sqrt {14} }}{2}

    Vậy {S_{\Delta SAB}} = \frac{1}{2}AB.SM = \frac{{{R^2}\sqrt 7 }}{2} (đvdt).

  • Câu 6: Vận dụng
    Độ dài đường sinh

    Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và \widehat {SAO} = {30^0},\widehat {SAB} = {60^0}. Độ dài đường sinh \ell của hình nón bằng:

    Hướng dẫn:

     Độ dài đường sinh

    Gọi I là trung điểm AB, suy ra OI \bot AB,{m{ }}SI \bot AB và OI = a.

    Trong tam giác vuông SOA, ta có OA = SA.\cos \widehat {SAO} = \frac{{SA\sqrt 3 }}{2}

    Trong tam giác vuông SIA, ta có IA = SA.\cos \widehat {SAB} = \frac{{SA}}{2}

    Trong tam giác vuông OIA, ta có:

    O{A^2} = O{I^2} + I{A^2} \Leftrightarrow \frac{3}{4}S{A^2} = {a^2} + \frac{1}{4}S{A^2} \Rightarrow SA = a\sqrt 2 .

  • Câu 7: Nhận biết
    Thể tích khối trụ

    Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng a. Thể tích khối trụ bằng:

    Hướng dẫn:

     Do thiết diện đi qua trục hình trụ nên ta có h=a.

    Bán kính đáy R = \frac{a}{2}. Do đó thể tích khối trụ V = {R^2}\pi .h = \frac{{\pi {a^3}}}{4}(đvtt).

  • Câu 8: Thông hiểu
    Tính tang của góc

    Cho hình nón có đỉnh S, đường cao SO = h, đường sinh SA. Nội tiếp hình nón là một hình chóp đỉnh S, đáy là hình vuông ABCD cạnh a. Nửa góc ở đỉnh của hình nón có tan bằng:

    Hướng dẫn:

     Tính tang của góc

    Nửa góc ở đỉnh của hình nón là góc \widehat {ASO} .

    Hình vuông ABCD cạnh a nên suy ra: OA = \frac{{a\sqrt 2 }}{2}

    Trong tam giác vuông SOA, ta có \tan \widehat {ASO} = \frac{{OA}}{{SO}} = \frac{{a\sqrt 2 }}{{2h}}.

  • Câu 9: Nhận biết
    Tính diện tích

    Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R\sqrt 3. Diện tích xung quanh và diện tích toàn phần của hình lần lượt có giá trị là:

    Hướng dẫn:

    Diện tích xung quanh của hình trụ: {S_{xq}} = 2\pi R.R\sqrt 3 = 2\sqrt 3 \pi {R^2}(đvdt).

    Diện tích toàn phần của hình trụ:

    {S_{tp}} = {S_{xq}} + 2.{S_{{m{day}}}} = 2\sqrt 3 \pi {R^2} + 2\left( {\pi {R^2}} ight) = 2\left( {\sqrt 3 + 1} ight)\pi {R^2}(đvdt).

  • Câu 10: Vận dụng
    Tính bán kính đáy

    Cho hình trụ có hai đáy là hai hình tròn (O) và(O’), thiết diện qua trục của hình trụ là hình vuông. Gọi A, B là hai điểm lần lượt nằm trên hai đường tròn (O) và(O’). Biết AB = 2a và khoảng cách giữa hai đường thẳng AB và OO’ bằng \frac{{a\sqrt 3 }}{2}. Bán kính đáy bằng:

    Hướng dẫn:

     Tính bán kính

    Dựng đường sinh BB', gọi I là trung điểm của AB’, ta có

    \left\{ \begin{array}{l}OI \bot AB'\\OI \bot BB'\end{array} ight. \Rightarrow OI \bot \left( {ABB'} ight)

    Suy ra d\left[ {AB,OO'} ight] = d\left[ {OO',\left( {ABB'} ight)} ight] = d\left[ {O,\left( {ABB'} ight)} ight] = OI = \frac{{a\sqrt 3 }}{2}.

    Gọi bán kính đáy của hình trụ là R.

    Vì thiết diện qua trục của hình trụ là hình vuông nên OO' = BB' = 2R

    Trong tam giác vuông A B’B, ta có AB{'^2} = A{B^2} - B{B^2} = 4{a^2} - 4{R^2}.

    Trong tam giác vuông OIB’, ta có N OB{'^2} = O{I^2} + IB{'^2} \Leftrightarrow {R^2} = {\left( {\frac{{a\sqrt 3 }}{2}} ight)^2} + {\left( {\frac{{AB'}}{2}} ight)^2}.

    Suy ra AB{'^2} = 4{R^2} - 3{a^2}.

    Từ đó ta có 4{a^2} - 4{R^2} = 4{R^2} - 3{a^2} \Rightarrow R = \frac{{a\sqrt {14} }}{4}.

  • Câu 11: Thông hiểu
    Thể tích của khối trụ

    Cho hình trụ có chiều cao bằng 8a . Biết hai điểm A và C lần lượt nằm trên hai đáy thỏa mãn AC=10a, khoảng cách giữa AC và trục của hình trụ bằng 4a. Thể tích của khối trụ đã cho là:

    Hướng dẫn:

      Thể tích của khối trụ

    Gọi (O) và (O') lần lượt là hai đường tròn đáy; A\in (O), C \in (O') .

    Dựng AD, CB lần lượt song song với OO' (D \in (O'), B \in (O). Dễ dàng có ABCD là hình chữ nhật.

    Do AC=10a,AD=8a\Rightarrow DC=6a..

    Gọi H là trung điểm của DC.

    \left\{\begin{matrix}O^\prime H\bot D C\\O^\prime H\bot A D\\\end{matrix}\Rightarrow O^\prime H\bot(ABCD)ight..

    Ta có O^\prime//(ABCD)\Rightarrow d\left(OO^\prime,ACight)=d\left(OO^\prime,(ABCD)ight)=O^\prime H=4a..

    Suy ra O^\prime H=4a,CH=3a\Rightarrow R=O^\prime C=5a..

    Vậy thể tích của khối trụ là V=\pi R^2h=\pi(5a)^28a=200\pi a^3.

  • Câu 12: Vận dụng
    Tỉ số giữa thể tích

    Một hình nón có đường cao bằng 9 cm nội tiếp trong một hình cầu bán kính bằng 5 cm. Tỉ số giữa thể tích khối nón và khối cầu là:

    Hướng dẫn:

    Tỉ số giữa thể tích

    Hình vẽ kết hợp với giả thiết, ta có SH = 9cm, OS=OA=5cm

    Suy ra OH = 4{m{cm}} và AH = \sqrt {O{A^2} - O{H^2}} = 3{m{cm}}{m{.}}

    Thể tích khối nón {V_n} = \frac{1}{3}\pi A{H^2}.SH = 27\pi(đvtt).

    Thể tích khối cầu {V_c} = \frac{4}{3}\pi .S{O^3} = \frac{{500\pi }}{3}  (đvtt).

    Suy ra \frac{{{V_n}}}{{{V_c}}} = \frac{{81}}{{500}}

  • Câu 13: Vận dụng cao
    Thể tích khối cầu nội tiếp hình nón

    Cho hình nón có bán kính đáy là 5a , độ dài đường sinh là 13a. Thể tích khối cầu nội tiếp hình nón bằng:

    Hướng dẫn:

    Thể tích khối cầu nội tiếp hình nón

    Xét mặt phẳng qua trục SO của hình nón ta được thiết diện là tam giác cân SAB.

    Mặt phẳng đó cắt mặt cầu theo đường tròn có bán kính r (bán kính mặt cầu) và nội tiếp trong tam giác cân SAB.

    Trong tam giác vuông SOB, gọi I là giao điểm của đường phân giác trong góc B với đường thẳng SO.

    Chứng minh được I là tâm đường tròn nội tiếp tam giác và bán kínhr =IO=IE  (E là hình chiếu vuông góc của I trên SB).

    Theo tính chất phân giác, ta có \frac{{IS}}{{IO}} = \frac{{BS}}{{BO}} = \frac{{13}}{5}.

    Lại có IS + IO = SO = \sqrt {S{B^2} - O{B^2}} = 12.

    Từ đó suy ra IS = \frac{{26}}{3},{m{ }}IO = \frac{{10}}{3}.

    Ta có \Delta SEI \backsim\Delta SOB  nên \frac{{IE}}{{IS}} = \frac{{BO}}{{BS}} = \frac{5}{{13}} \Rightarrow IE = \frac{5}{{13}}IS = \frac{{10}}{3}

    Thể tích khối cầu: V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {\left( {\frac{{10a}}{3}} ight)^3} = \frac{{4000\pi {a^3}}}{{81}} (đvtt).

  • Câu 14: Thông hiểu
    Diện tích toàn phần

    Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Diện tích toàn phần của hình trụ bằng:

    Hướng dẫn:

    Diện tích toàn phần

    Theo giả thiết ta được hình trụ có chiều cao h=AB=1 , bán kính đáy R = \frac{{AD}}{2} = 1

    Do đó diện tích toàn phần: {S_{tp}} = 2\pi Rh + 2\pi {R^2} = 4\pi

  • Câu 15: Nhận biết
    Độ dài đường sinh

    Cho mặt cầu tâm O, bán kính R = a. Một hình nón có đỉnh S là ở trên mặt cầu và đáy là đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho SH = \frac{{3a}}{2}. Độ dài đường sinh \ell của hình nón bằng:

    Hướng dẫn:

    Độ dài đường sinh

    Gọi S' là điểm đối xứng của S qua tâm O và A là một điểm trên đường tròn đáy của hình nón.

    Tam giác SAS’ vuông tại A và có đường cao AH nên S{A^2} = SH.SS' \Rightarrow SA = a\sqrt 3 .

  • Câu 16: Thông hiểu
    Tính đường cao

    Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB, biết AB chắn trên đường tròn đáy một cung có số đo bằng 60^0, khoảng cách từ tâm O đến mặt phẳng (SAB) bằng \frac{R}{2}. Đường cao h của hình nón bằng:

    Hướng dẫn:

    Theo giả thiết ta có tam giác OAB đều cạnh R.

    Gọi E là trung điểm AB, suy ra OE \bot AB và OE = \frac{{R\sqrt 3 }}{2}.

    Gọi H là hình chiếu của O trên SE, suy ra OH \bot SE.

    Ta có \left\{ \begin{array}{l}AB \bot OE\\AB \bot SO\end{array} ight. \Rightarrow AB \bot \left( {SOE} ight) \Rightarrow AB \bot OH

    Từ đó suy ra OH \bot \left( {SAB} ight) nên d\left[ {O,\left( {SAB} ight)} ight] = OH = \frac{R}{2}.

    Trong tam giác vuông SOE, ta có  \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{E^2}}} = \frac{8}{{3{R^2}}} \Rightarrow SO = \frac{{R\sqrt 6 }}{4}

  • Câu 17: Nhận biết
    Diện tích toàn phần

    Cạnh bên của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 120^0. Diện tích toàn phần của hình nón là:

    Hướng dẫn:

    Diện tích toàn phần

    Gọi S là đỉnh, O là tâm của đáy, thiết diện qua trục là SAB.

    Theo giả thiết, ta có SA = 2a và \widehat {ASO} = 60^\circ.

    Trong tam giác SAO vuông tại O, ta có

    OA = SA.\sin 60^\circ = a\sqrt 3

    Vậy diện tích toàn phần:

    {S_{tp}} = \pi R\ell + \pi {R^2} = \pi .OA.SA + \pi {\left( {OA} ight)^2} = \pi {a^2}\left( {3 + 2\sqrt 3 } ight) (đvdt).

  • Câu 18: Thông hiểu
    Tính bán kính đáy

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài đường sinh bằng 2a thì bán kính đáy bằng:

    Hướng dẫn:

     Gọi bán kính đáy là R.

    Từ giả thiết suy ra h= 2a và chu vi đáy bằng a .

    Do đó 2\pi R = a \Leftrightarrow R = \frac{a}{{2\pi }}.

  • Câu 19: Nhận biết
    Diện tích toàn phần

    Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh có cạnh bằng 2R. Diện tích toàn phần của khối trụ bằng:

    Hướng dẫn:

    Do thiết diện đi qua trục hình trụ nên ta có h = 2R.

    Diện tích toàn phần là: {S_{tp}} = 2\pi R\left( {R + h} ight) = 6\pi {R^2} (đvdt).

  • Câu 20: Vận dụng
    Tính đường cao nón

    Cho hình nón đỉnh S có đáy là hình tròn tâm O. Dựng hai đường sinh SA và SB, biết tam giác SAB vuông và có diện tích bằng 4a^2. Góc tạo bởi giữa trục SO và mặt phẳng (SAB) bằng 30^0. Đường cao h của hình nón bằng:

    Hướng dẫn:

     Tính đường cao nón

    Theo giả thiết ta có tam giác SAB vuông cân tại S.

    Gọi E là trung điểm AB, suy ra\left\{ \begin{array}{l}SE \bot AB\\OE \bot AB\end{array} ight.  và SE = \frac{1}{2}AB.

    Ta có {S_{\Delta SAB}} = \frac{1}{2}AB.SE = 4{a^2} \Leftrightarrow \frac{1}{2}AB.\frac{1}{2}AB = 4{a^2}

    \Rightarrow AB = 4a \Rightarrow SE = 2a.

    Gọi H là hình chiếu của O trên SE, suy ra OH \bot SE.

    Ta có \left\{ \begin{array}{l}AB \bot OE\\AB \bot SO\end{array} ight. \Rightarrow AB \bot \left( {SOE} ight) \Rightarrow AB \bot OH.

    Từ đó suy ra OH \bot \left( {SAB} ight) nên

    {30^0} = \widehat {SO,\left( {SAB} ight)} = \widehat {SO,SH} = \widehat {OSH} = \widehat {OSE}

    Trong tam giác vuông SOE, ta có SO = SE.\cos \widehat {OSE} = a\sqrt 3

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (30%):
    2/3
  • Thông hiểu (30%):
    2/3
  • Vận dụng (30%):
    2/3
  • Vận dụng cao (10%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 7 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập