Khái niệm về Khối đa diện

Bài học Lí thuyết toán 12: Khái niệm về khối đa diện mở đầu cho các em những kiến thức nền tảng về hình đa diện, khối đa diện, hai đa diện bằng nhau và các phép biến hình trong không gian.

1. Khối lăng trụ và khối chóp

1.1. Định nghĩa

1.2. Các yếu tố của khối lăng trụ, khối chóp

• Đỉnh, cạnh, mặt, mặt bên, mặt đáy, cạnh bên, cạnh đáy,... của một hình lăng trụ, hình chóp, chóp cụt theo thứ tự cũng là đỉnh, cạnh, mặt, mặt bên, mặt đáy, cạnh bên, cạnh đáy,... của một khối lăng trụ, khối chóp, chóp cụt.
• Điểm ngoài là điểm không thuộc khối lăng trụ, khối chóp, chóp cụt.
• Điểm trong là điểm thuộc khối lăng trụ, khối chóp, chóp cụt nhưng không thuộc hình lăng trụ, hình chóp, chóp cụt ứng với khối đó.

2. Khái niệm hình đa diện và khối đa diện

2.1. Hình đa diện

Định nghĩa:

2.2. Khối đa diện

Định nghĩa:

Ví dụ: Trong những hình sau, hình nào là hình đa diện?

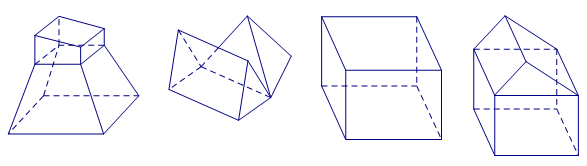Hình 1, Hình 3 và Hình 4 là những hình đa diện (từ trái sang phải)

Hình 2 không phải là hình đa diện vì đã vi phạm tính chất: Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

3. Hai đa diện bằng nhau

3.1. Phép dời hình trong không gian

Định nghĩa:

Một số phép dời hình:

• Phép tịnh tiến theo vecto
• Phép đối xúng qua mp (P)
• Phép đối xứng tâm O
• Phép đối xứng qua đường thẳng

3.2. Hai hình bằng nhau

Định nghĩa: Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

Ví dụ: Cho hình hộp

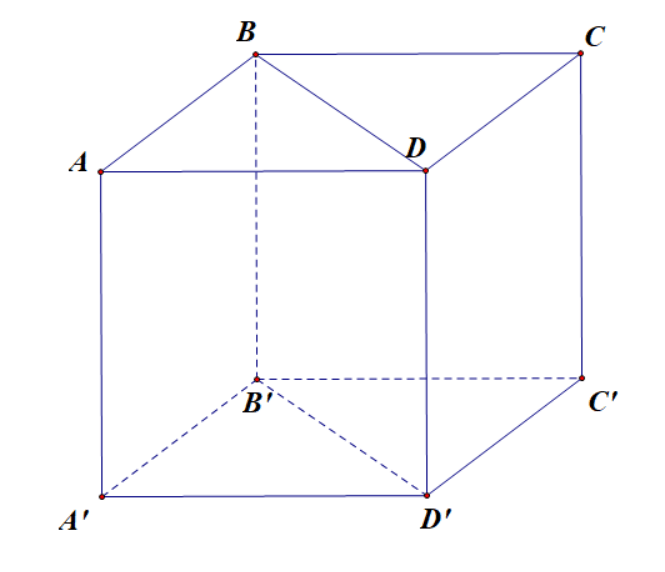
Phép đối xứng qua biến lăng trụ thành lăng trụ . Do đó, ta suy ra hai lăng trụ và là hai hình bằng nhau.

4. Phân chia lắp ghép các khối đa diện

Ví dụ: Cho khối lập phương . 

• Khi đó, chia khối lập phương thành hai khối lăng trụ và

• Khối lăng trụ có thể được tiếp tục phân chia thành khối chóp tam giác hay còn gọi là khối tứ diện và khối chóp tứ giác

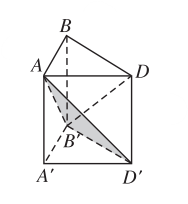
Nhận xét: Mọi khối đa diện bất kì luôn có thể phân chia được thành những khối tứ diện.