Cho hai điểm ![]() . Viết phương trình tổng quát của mặt phẳng
. Viết phương trình tổng quát của mặt phẳng ![]() vuông góc với AB, cắt ba trục tọa độ Ox, Oy, Oz tại M, N, E sao cho thể tích hình chóp
vuông góc với AB, cắt ba trục tọa độ Ox, Oy, Oz tại M, N, E sao cho thể tích hình chóp ![]() bằng
bằng ![]() đvtt.
đvtt.
Vecto pháp tuyến của
Phương trình
cắt 3 trục tọa độ tại
Thể tích hình chóp là:
Cho hai điểm ![]() . Viết phương trình tổng quát của mặt phẳng
. Viết phương trình tổng quát của mặt phẳng ![]() vuông góc với AB, cắt ba trục tọa độ Ox, Oy, Oz tại M, N, E sao cho thể tích hình chóp
vuông góc với AB, cắt ba trục tọa độ Ox, Oy, Oz tại M, N, E sao cho thể tích hình chóp ![]() bằng
bằng ![]() đvtt.
đvtt.
Vecto pháp tuyến của
Phương trình
cắt 3 trục tọa độ tại
Thể tích hình chóp là:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm ![]() và mặt phẳng
và mặt phẳng ![]() . Gọi M là điểm thuộc (P) sao cho
. Gọi M là điểm thuộc (P) sao cho ![]() vuông tại M . Khoảng cách từ M đến (Oxy) bằng:
vuông tại M . Khoảng cách từ M đến (Oxy) bằng:
Ta có: suy ra M thuộc mặt cầu (S) đường kính AB.
Gọi I là trung điểm AB , khi đó và
.
Ta tính được suy ra (P) và mặt cầu (S) tiếp xúc nhau hay M là tiếp điểm của (P) và (S). Vậy M là hình chiếu của I trên (P) .
Phương trình đường thẳng qua I và vuông góc với (P) là:
Tọa độ của M là nghiệm của hệ phương trình:
suy ra .
Suy ra .
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2;2;0), B(1;0;-2) và mặt
phẳng![]() . Gọi
. Gọi ![]() là điểm thuộc mặt phẳng (P) sao cho MA=MB
là điểm thuộc mặt phẳng (P) sao cho MA=MB
và góc ![]() có số đo lớn nhất. Khi đó giá trị
có số đo lớn nhất. Khi đó giá trị ![]() bằng ?
bằng ?
nên M thuộc mặt phẳng mặt phẳng trung trực của đoạn thẳng AB. Ta có phương trình trung trực của AB là (Q); y+z=0
M thuộc giao tuyến của hai mặt phẳng (P) và (Q) nên M thuộc đường thẳng
.
Gọi , ta có
.
Khảo sát hàm số , ta được
khi
.
Suy ra có số đo lớn nhất khi
, ta có
.
Khi đó giá trị .
Cho tam giác ABC với ![]() .
.
Viết phương trình tổng quát của mặt phẳng ![]() vuông góc với mặt phẳng
vuông góc với mặt phẳng ![]() song song đường cao AH của tam giác ABC.
song song đường cao AH của tam giác ABC.
Theo đề bài, ta có: song song đường cao
Trong không gian với hệ tọa độ ![]() cho điểm
cho điểm ![]() và mặt phẳng
và mặt phẳng ![]() , m là tham số. Gọi là hình chiếu vuông góc của điểm trên . Tính khi khoảng cách từ điểm đến lớn nhất ?
, m là tham số. Gọi là hình chiếu vuông góc của điểm trên . Tính khi khoảng cách từ điểm đến lớn nhất ?
Ta có
Xét hàm số
Ta lập bảng biến thiên cho hàm số trên, được:
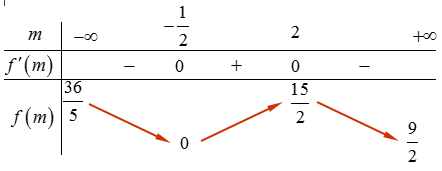
Qua bảng biến thiên, ta thấy hàm số đạt GTLN khi
Đường thẳng qua A và vuông góc với (P) có phương trình là
Ta có
Trong không gian hệ tọa độ Oxyz, cho điểm ![]() và mặt phẳng
và mặt phẳng ![]() . Gọi
. Gọi ![]() thuộc
thuộc ![]() sao cho
sao cho ![]() đạt giá trị nhỏ nhất. Tính tổng
đạt giá trị nhỏ nhất. Tính tổng ![]() .
.
Giả sử là điểm thỏa mãn
.
Khi đó ,
,
;
;
;
(vì
)
Vì I cố định nên đạt giá trị nhỏ nhất khi MI nhỏ nhất, khi đó M là hình chiếu vuông góc của I lên
.
Gọi là đường thẳng qua I và vuông góc với
Phương trình đường thẳng .
Tọa độ của M là nghiệm hệ phương trình:
.
Phương trình tổng quát của mặt phẳng đi qua ![]() và song song với vectơ
và song song với vectơ ![]() là:
là:
Theo đề bài, ta có:
Chọn làm 1 vectơ pháp tuyến.
Phương trình mặt phẳng cần tìm có dạng :
Mà mp lại qua A nên
Phương trình cần tìm là: .
Cho hai điểm![]() và vectơ
và vectơ ![]() . Mặt phẳng chứa hai điểm A, B và song song với vectơ
. Mặt phẳng chứa hai điểm A, B và song song với vectơ ![]() có phương trình:
có phương trình:
Theo đề bài, ta có:
Như vậy, và
sẽ là cặp vectơ chỉ phương của
Chọn làm vectơ pháp tuyến của
Phương trình mặt phẳng có dạng
Mặt khác, vì điểm nên thay tọa độ điểm A vào phương trình mặt phẳng
được:
Vậy có phương trình là:
Cho mặt phẳng ![]() qua điểm
qua điểm ![]() và chắn trên ba trục tọa độ
và chắn trên ba trục tọa độ ![]() theo ba đoạn có số đo đại số a, b, c. Viết phương trình tổng quát của
theo ba đoạn có số đo đại số a, b, c. Viết phương trình tổng quát của ![]() khi a, b, c tạo thành một cấp số nhân có công bội bằng 2.
khi a, b, c tạo thành một cấp số nhân có công bội bằng 2.
Theo đề bài, ta có a, b, c là cấp số nhân với công bội q=2
Phương trình của
(P) qua
Cho tứ giác ABCD có ![]() . Viết phương trình của mặt phẳng (P) qua A, B và chia tứ diện thành hai khối ABCE và ABDE có tỉ số thể tích bằng 3.
. Viết phương trình của mặt phẳng (P) qua A, B và chia tứ diện thành hai khối ABCE và ABDE có tỉ số thể tích bằng 3.

Theo đề bài, ta có mp (P) cắt cạnh CD tại E, E chia đoạn CD theo tỷ số -3
Từ đó, ta suy ra:
Như vậy, VTPT mp (P) là:
Viết phương trình tổng quát của mặt phẳng (P) qua giao tuyến của hai mặt phẳng ![]() và vuông góc với mặt phẳng
và vuông góc với mặt phẳng ![]()
Theo đề bài, qua giao tuyến của hai mặt phẳng
nên
có dạng là
Chọn làm vectơ pháp tuyến của
, ta có:
Cho hai mặt phẳng ![]() .
.
Gọi ![]() là góc nhọn tạo bởi
là góc nhọn tạo bởi ![]() và
và ![]() thì giá trị đúng của
thì giá trị đúng của ![]() là:
là:
Theo đề bài đã cho PTTQ , ta suy ra được các vecto pháp tuyến tương ứng là:
có vectơ pháp tuyến
có vectơ pháp tuyến
Áp dụng công thức tính cosin giữa 2 vecto, ta có:
Cho hai mặt phẳng ![]() và
và ![]() . Với
. Với ![]() cho biết
cho biết ![]() và cặp vectơ chỉ phương
và cặp vectơ chỉ phương ![]() . Với
. Với ![]() cho PTTQ
cho PTTQ ![]() . Phương trình tổng quát của mặt phẳng (P) chứa giao tuyến của
. Phương trình tổng quát của mặt phẳng (P) chứa giao tuyến của ![]() và
và ![]() , qua điểm
, qua điểm ![]() là:
là:
Trước tiên, ta cần đưa phương trình về dạng tổng quát.
Theo đề bài, ta có và cặp vectơ chỉ phương
nên vecto pháp tuyến của mp
là tích có hướng của 2 vecto chỉ phương.
Ta có .
Chọn làm vectơ pháp tuyến cho
thì phương trình tổng quát của
có dạng
.
Vậy phương trình
Để tìm phương trình tổng quát của mặt phẳng (P) chứa giao tuyến của và
ta xét chùm mặt phẳng :
Mặt khác, ta có
Thế vào (*) ta được:
Viết phương trình tổng quát của mặt phẳng (P) qua ba điểm ![]()
Theo đề bài, ta có cặp vecto chỉ phương của
Từ đó, ta suy ra vecto pháp tuyến của (P) là tích có hướng của 2 VTCP của
Mp (P) đi qua và nhận vecto có tọa độ
làm 1 VTPT có phương trình là:
Ba mặt phẳng ![]() cắt nhau tại điểm A. Tọa độ của điểm A đó là:
cắt nhau tại điểm A. Tọa độ của điểm A đó là:
Tọa độ giao điểm của ba mặt phẳng là nghiệm của hệ phương trình :
Giải (1),(2) tính theo
được
.
Thế vào phương trình (3) được , từ đó có
Vậy .
Phương trình tổng quát của mặt phẳng qua A(3,-1, 2), B(4, -2, -1), C(2, 0, 2) là:
Theo đề bài, ta có được các vecto sau:
Vì mặt phẳng đi qua 3 điểm nên VTPT của mp là tích có hướng của và
.
Chọn làm một vectơ pháp tuyến.
Phương trình mp có dạng
là mp qua A
Vậy phương trình .
Viết phương trình tổng quát của mặt phẳng (P) qua hai điểm ![]() và có một vectơ chỉ phương
và có một vectơ chỉ phương ![]() .
.
Theo đề bài ta có:
Như vậy, VTPT của (P) là tích có hướng của 2 vecto chỉ phương
Mp (P) đi qua và nhận vecto
làm 1 VTPT có phương trình là:
Trong không gian với hệ tọa độ ![]() , mặt phẳng
, mặt phẳng ![]() qua hai điểm
qua hai điểm ![]() cắt các nửa trục dương Ox, Oy lần lượt tại A, B sao cho OG nhỏ nhất (G là trọng tâm tam giác ABC). Biết
cắt các nửa trục dương Ox, Oy lần lượt tại A, B sao cho OG nhỏ nhất (G là trọng tâm tam giác ABC). Biết ![]() . Tính
. Tính ![]() .
.
Gọi mà
nên
và
.
qua hai điểm
nên
.
Ta có:
Suy ra
Dấu bằng xảy ra khi và chỉ khi:
Cho 3 mặt phẳng ![]() . Mặt phẳng
. Mặt phẳng ![]() chứa giao tuyến của
chứa giao tuyến của ![]() ,vuông góc với
,vuông góc với ![]() có phương trình tổng quát:
có phương trình tổng quát:
Mặt phẳng thuộc chùm mặt phẳng
nên phương trình có dạng:
Vì vuông góc với
nên ta được:
Vậy ta có phương trình là :
Cho biết có n mặt phẳng với phương trình tương ứng là ![]() với
với ![]() đi qua điểm
đi qua điểm ![]() và không đi qua gốc tọa độ O , đồng thời cắt các trục tọa độ
và không đi qua gốc tọa độ O , đồng thời cắt các trục tọa độ ![]() theo thứ tự tại A, B, C sao cho hình chóp OABC là hình chóp đều. Khi đó giá trị
theo thứ tự tại A, B, C sao cho hình chóp OABC là hình chóp đều. Khi đó giá trị ![]() bằng?
bằng?
Giả sử mặt phẳng thỏa mãn yêu cầu bài toán
+) Ta có:
.
Vì hình chóp OABC là hình chóp đều, suy ra
Nên ta có (do (P) không đi qua gốc tọa độ nên
)
+) Vì điểm nên suy ra:
Nhận thấy nếu thì
, trường hợp này không thỏa mãn do
Như vậy ta sẽ có 3 mặt phẳng thỏa mãn yêu cầu bài toán lần lượt ứng với các trường hợp và
Vậy suy ra
.
