Khối đa diện lồi và Khối đa diện đều

Bài học Lí thuyết toán 12: Khối đa diện lồi và khối đa diện đều bao gồm khái niệm về khối đa diện lồi, đa diện đều và các tính chất của 5 loại khối đa diện đều. Hi vọng các em sẽ ôn tập hiệu quả, hướng đến đạt mục tiêu trong các kì thi lớn sắp tới.

1. Khối đa diện lồi

Định nghĩa:

Ví dụ:

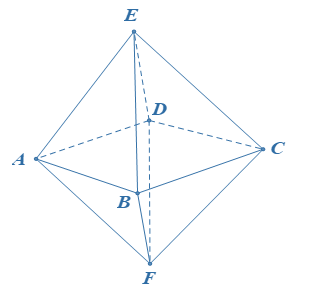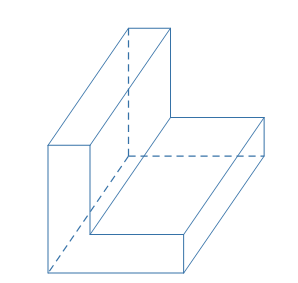Khối đa diện lồi	Khối đa diện không lồi

2. Khối đa diện đều

2.1. Định nghĩa

2.2. Định lí

Tùy theo số mặt của chúng, 5 khối đa diện trên có tên gọi là:

Khối tứ diện đều; khối lập phương; khối bát diện đều; khối mười hai mặt đều; khối hai mươi mặt đều.

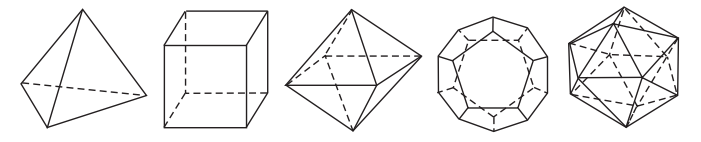
2.3. Bảng tóm tắt của năm loại khối đa diện đều

Chú ý:

Giả sử khối đa diện đều loại có D đỉnh, C cạnh và M mặt.

• Khi đó, ta có công thức sau:

• Định lý Ơ - le: Mọi khối đa diện lồi đều có: 

3. Một số kết quả quan trọng về khối đa diện lồi

3.1. Kết quả 1

3.2. Kết quả 2

• Tâm của các mặt của một khối lập phương là các đỉnh của một khối bát diện đều.
• Tâm của các mặt của một khối bát diện đều là các đỉnh của một khối lập phương.

3.3. Kết quả 3

Khi đó:

• Ba đường chéo cắt nhau tại trung điểm của mỗi đường;
• Ba đường chéo đôi một vuông góc với nhau;
• Ba đường chéo bằng nhau.