Tìm tập hợp các tâm I của mặt cầu sau nằm trên?
![]()
Theo đề bài, ta xác định các hệ số của :
Suy ra ta gọi được tâm I của mặt cầu có tọa độ là
Xét là mặt cầu
Vậy tập hợp các điểm I là phân đường thẳng
tương ứng với .
Tìm tập hợp các tâm I của mặt cầu sau nằm trên?
![]()
Theo đề bài, ta xác định các hệ số của :
Suy ra ta gọi được tâm I của mặt cầu có tọa độ là
Xét là mặt cầu
Vậy tập hợp các điểm I là phân đường thẳng
tương ứng với .
Cho mặt cầu ![]() và mặt phẳng
và mặt phẳng ![]() . Biết khoảng cách từ O đến
. Biết khoảng cách từ O đến ![]() bằng
bằng ![]() . Khi đó thiết diện tạo bởi mặt phẳng
. Khi đó thiết diện tạo bởi mặt phẳng ![]() với
với ![]() là một đường tròn có đường kính bằng:
là một đường tròn có đường kính bằng:
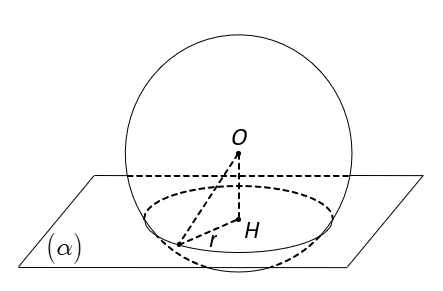
Gọi H là hình chiếu của O xuống .
Ta có nên
cắt
theo đường tròn
.
Bán kính đường tròn là
Suy ra đường kính bằng .
Cho lăng trụ đứng ![]() có đáy ABC là tam giác vuông tại B,
có đáy ABC là tam giác vuông tại B, ![]() , góc
, góc ![]() bằng
bằng ![]() . Góc giữa đường thẳng
. Góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() . Bán kính mặt cầu ngoại tiếp tứ diện
. Bán kính mặt cầu ngoại tiếp tứ diện ![]() bằng:
bằng:
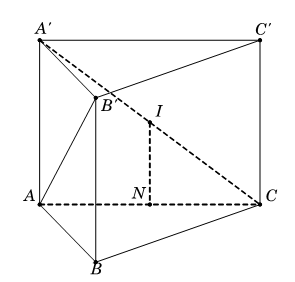
Ta có .
Trong , ta có
Trong , ta có
Gọi N là trung điểm AC , suy ra N là tâm đường tròn ngoại tiếp .
Gọi là trung điểm A'C, suy ra
.
Do đó IN là trục của , suy ra
(1)
Hơn nữa, tam giác vuông tại A có
là trung điểm A'C nên
. (2)
Từ (1) và (2), ta có hay
là tâm của mặt cầu ngoại tiếp hình chóp
với bán kính
.
Trong không gian cho ba điểm ![]() và
và ![]() . Biết mặt
. Biết mặt
phẳng qua ![]() và tâm mặt cầu nội tiếp tứ diện
và tâm mặt cầu nội tiếp tứ diện ![]() có một vectơ pháp tuyến là
có một vectơ pháp tuyến là ![]() . Tổng
. Tổng ![]() là?
là?
Áp dụng phương pháp tìm tọa độ tâm của mặt cầu nội tiếp tứ diện.
Phương trình là:
Phương trình là:
.
Phương trình là:
Phương trình là:
.
Gọi là tâm mặt cầu nội tiếp tứ diện
.
Do đó:
nằm cùng phía với A đối với
suy ra:
.
nằm cùng phía với B đối với
suy ra:
.
nằm cùng phía với C đối với
suy ra:
.
nằm cùng phía với O đối với
suy ra:
.
Suy ra:
Suy ra: ,
cùng phương với .
Suy ra có một VTPT là
.
Vậy: .
Cho hình chóp ![]() có đáy ABC là tam giác vuông tại B và
có đáy ABC là tam giác vuông tại B và ![]() . Cạnh bên
. Cạnh bên ![]() và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp
và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp ![]() là:
là:
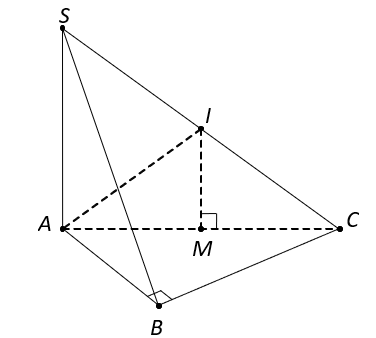
Gọi M là trung điểm AC, suy ra M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi I là trung điểm SC, suy ra nên
.
Do đó IM là trục của , suy ra
(1)
Hơn nữa, tam giác SAC vuông tại A có I là trung điểm SC nên . (2)
Từ (1) và (2) , ta có
hay I là tâm của mặt cầu ngoại tiếp hình chóp .
Vậy bán kính .
Trong không gian với hệ tọa độ ![]() cho mặt cầu
cho mặt cầu ![]() và điểm
và điểm ![]() . Ba mặt phẳng thay đổi đi qua
. Ba mặt phẳng thay đổi đi qua ![]() và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.
và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.
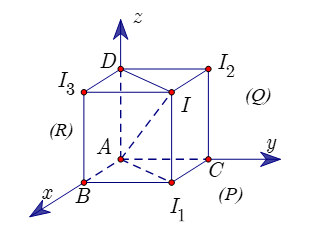
Giả sử ba mặt mặt phẳng cùng đi qua A đôi một vuông góc với nhau là
Với điểm I bất kỳ, hạ lần lượt vuông góc với ba mặt phẳng
thì ta luôn có:
(1) .
Ta sẽ chứng minh (1) và áp dụng vào giải bài toán.

Giả sử ba mặt mặt phẳng cùng đi qua A đôi một vuông góc với nhau là
Với điểm I bất kỳ, hạ lần lượt vuông góc với ba mặt phẳng
thì ta luôn có:
(1) .
Thật vậy , ta chọn hệ trục tọa độ Oxyz với , ba trục Ox, Oy, Oz lần lượt là ba giao tuyến của ba mặt phẳng
.
Khi đó tọa độ I(a;b;c) thì:
hay .
Vậy (1) được chứng minh.
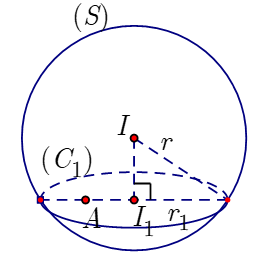
Áp dụng giải bài:
Mặt cầu (S) có tâm và có bán kính
.
.
Giả sử ba mặt mặt phẳng cùng đi qua A đôi một vuông góc với nhau là và cắt mặt cầu (S) theo ba đường tròn lần lượt là
.
Gọi và
lần lượt là tâm và bán kính của
.
Khi đó : .
Tương tự có: và
.
Theo nhận xét ở trên ta có:
Ta có tổng diện tích các đường tròn là :
.
Cho hình chóp tứ giác đều ![]() có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc
có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc ![]() . Thể tích của khối cầu ngoại tiếp khối chóp
. Thể tích của khối cầu ngoại tiếp khối chóp ![]() là:
là:
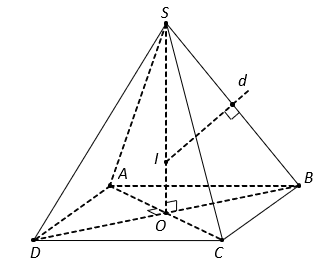
Gọi , suy ra
.
Ta có .
Trong , ta có
.
Ta có SO là trục của hình vuông ABCD.
Trong mặt phẳng SOB, kẻ đường trung trực d của đoạn B.
Gọi
Xét có
đều.
Do đó d cũng là đường trung tuyến của . Suy ra I là trọng tâm
.
Bán kính mặt cầu .
Suy ra
Cho mặt cầu ![]() và một điểm A, biết
và một điểm A, biết ![]() . Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
Vì AB tiếp xúc với (S) tại B nên .
Suy ra
Cho lăng trụ đứng ![]() có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc
có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc ![]() và điểm G là trọng tâm tam giác ABC. Bán kính mặt cầu ngoại tiếp khối chóp
và điểm G là trọng tâm tam giác ABC. Bán kính mặt cầu ngoại tiếp khối chóp ![]() bằng:
bằng:
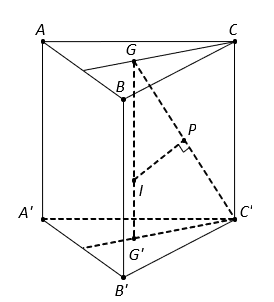
Gọi M là trung điểm B’C’, ta có
.
Trong , có
;
.
Gọi G’ là trọng tâm tam giác đều A’B’C’, suy ra G’ cũng là tâm đường tròn ngoại tiếp .
Vì lặng trụ đứng nên .
Do đó là trục của tam giác
.
Trong mặt phẳng , kẻ trung trực d của đoạn thẳng
cắt
tại I. Khi đó I là tâm mặt cầu ngoại tiếp khối chóp
, bán kính
Ta có
.
Cho mặt cầu S(O;R) , A là một điểm ở trên mặt cầu (S) và (P) là mặt phẳng qua A sao cho góc giữa OA và (P) bằng ![]() . Diện tích của đường tròn giao tuyến bằng:
. Diện tích của đường tròn giao tuyến bằng:
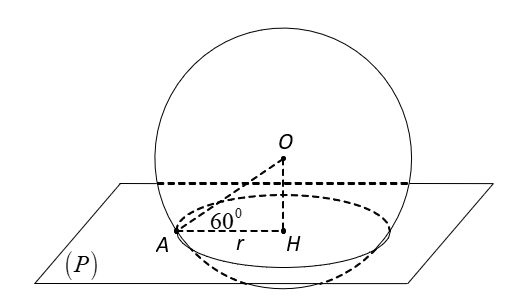
Gọi H là hình chiếu vuông góc của (O) trên (P) thì
● H là tâm của đường tròn giao tuyến của (P) và (S).
●
Bán kính của đường tròn giao tuyến: .
Suy ra diện tích đường tròn giao tuyến: .
Cho mặt cầu ![]() và một điểm A, biết
và một điểm A, biết ![]() . Qua A kẻ một cát tuyến cắt (S) tại B và C sao cho
. Qua A kẻ một cát tuyến cắt (S) tại B và C sao cho ![]() . Khi đó khoảng cách từ O đến BC bằng:
. Khi đó khoảng cách từ O đến BC bằng:
Gọi H là hình chiếu của O lên BC.
Ta có , suy ra H là trung điểm của BC nên
Suy ra
Cho hai mặt cầu sau:
![]()
![]()
Xét vị trí tương đối của 2 mặt cầu?
Tiếp xúc trong || tiếp xúc trong
Cho hai mặt cầu sau:
Xét vị trí tương đối của 2 mặt cầu?
Tiếp xúc trong || tiếp xúc trong
Theo đề bài, ta suy ra các hệ số, tâm và bán kính của (S):
Tâm
bán kính
Tâm
; bán kính
(S) và (S') tiếp xúc trong.
Với giá trị nào của m thì mặt phẳng ![]() tiếp xúc với mặt cầu
tiếp xúc với mặt cầu
![]()
Theo đề bài, ta xác định các hệ số của (S):
Suy ra tâm I của cầu có tọa độ là .
tiếp xúc (S) khi:
(loại)
Cho mặt phẳng ![]() và mặt cầu
và mặt cầu ![]() . Xét vị trí tương đối của mặt phẳng với mặt cầu?Cắt nhau || cắt nhau
. Xét vị trí tương đối của mặt phẳng với mặt cầu?Cắt nhau || cắt nhau
Cho mặt phẳng và mặt cầu
. Xét vị trí tương đối của mặt phẳng với mặt cầu?Cắt nhau || cắt nhau
Theo đề bài, ta xác định các hệ số của (S):
Suy ra tâm I có tọa độ là:
Áp dụng CT, ta có (P) cắt (S)
Cho mặt cầu ![]() và mặt phẳng
và mặt phẳng ![]() . Gọi (C) là đường tròn giao tuyến của (P) và (S). Tính tọa độ tâm H của (C).
. Gọi (C) là đường tròn giao tuyến của (P) và (S). Tính tọa độ tâm H của (C).
Theo đề bài, mặt cầu (S) có tâm và vecto pháp tuyến của
Cho hình chóp ![]() có đáy
có đáy ![]() là tam giác vuông tại C và
là tam giác vuông tại C và ![]() . Mặt phẳng
. Mặt phẳng ![]() vuông góc với đáy,
vuông góc với đáy, ![]() ,
, ![]() . Bán kính mặt cầu ngoại tiếp hình chóp
. Bán kính mặt cầu ngoại tiếp hình chóp ![]() là:
là:
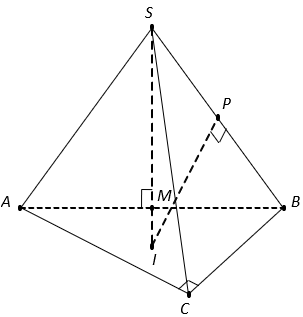
Gọi M là trung điểm AB , suy ra và
.
Do đó SM là trục của tam giác ABC.
Trong mặt phẳng , kẻ đường trung trực d của đoạn SB cắt SM tại I . Khi đó I là tâm mặt cầu ngoại tiếp hình chóp
, bán kính
Ta có
Trong tam giác vuông SMB, ta có .
Ta có , suy ra
Cho hình chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh a. Cạnh bên
là hình vuông cạnh a. Cạnh bên ![]() và vuông góc với đáy (
và vuông góc với đáy (![]() ). Tính theo
). Tính theo ![]() diện tích mặt cầu ngoại tiếp hình chóp
diện tích mặt cầu ngoại tiếp hình chóp ![]() ta được:
ta được:
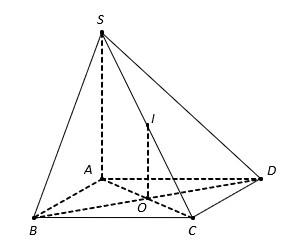
Gọi , suy ra O là tâm đường tròn ngoại tiếp hình vuông
.
Gọi I là trung điểm SC, suy ra
Do đó IO là trục của hình vuông , suy ra
(1)
Xét tam giác SAC vuông tại A có I là trung điểm cạnh huyền SC nên . (2)
Từ (1) và (2), ta có:
Vậy diện tích mặt cầu (đvdt).
Cho hình chóp tam giác đều ![]() có cạnh đáy bằng a và cạnh bên bằng
có cạnh đáy bằng a và cạnh bên bằng ![]() . Gọi h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số
. Gọi h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số ![]() bằng:
bằng:
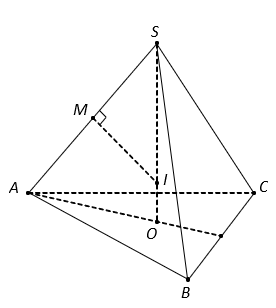
Gọi O là tâm , suy ra
và
Trong SOA, ta có
Trong mặt phẳng SOA, kẻ trung trực d của đoạn SA cắt SO tại I, suy ra:
Do đó nên I là tâm mặt cầu ngoại tiếp khối chóp .
Gọi M là tung điểm SA, ta có nên
Vậy
Trong không gian với hệ tọa độ ![]() , cho ba điểm
, cho ba điểm ![]() với
với ![]() . Biết rằng mặt phẳng
. Biết rằng mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() và tiếp xúc với mặt cầu
và tiếp xúc với mặt cầu ![]() . Tính
. Tính ![]() .
.
Mặt phẳng đi qua ba điểm
nên có phương trình là:
Ta có nên
.
Mặt cầu (S) có tâm và bán kính
.
tiếp xúc với (S)
Cho mặt cầu tâm I bán kính ![]() . Một mặt phẳng cắt mặt cầu và cách tâm I một khoảng bằng
. Một mặt phẳng cắt mặt cầu và cách tâm I một khoảng bằng ![]() . Thế thì bán kính của đường tròn do mặt phẳng cắt mặt cầu tạo nên là:
. Thế thì bán kính của đường tròn do mặt phẳng cắt mặt cầu tạo nên là:
Theo đề bài, mặt phẳng cắt mặt cầu theo một đường tròn
.
Vậy .
