Cho hình hộp chữ nhật ![]() có
có![]() . Tính theo
. Tính theo ![]() thể tích khối hộp đã cho.
thể tích khối hộp đã cho.
Áp dụng công thức tính thể tích khối hộp chữ nhật là:
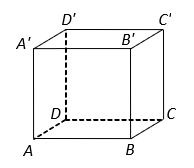
Trong tam giác vuông , có
.
Diện tích hình chữ nhật là
.
Vậy
Cho hình hộp chữ nhật ![]() có
có![]() . Tính theo
. Tính theo ![]() thể tích khối hộp đã cho.
thể tích khối hộp đã cho.
Áp dụng công thức tính thể tích khối hộp chữ nhật là:

Trong tam giác vuông , có
.
Diện tích hình chữ nhật là
.
Vậy
Cho lăng trụ ![]() có đáy
có đáy ![]() là hình thoi cạnh
là hình thoi cạnh ![]() , tâm O và
, tâm O và ![]() . Góc giữa cạnh bên
. Góc giữa cạnh bên ![]() và mặt đáy bằng
và mặt đáy bằng ![]() . Đỉnh A' cách đều các điểm A, B, D. Tính theo
. Đỉnh A' cách đều các điểm A, B, D. Tính theo ![]() thể tích
thể tích ![]() của khối lăng trụ đã cho.
của khối lăng trụ đã cho.
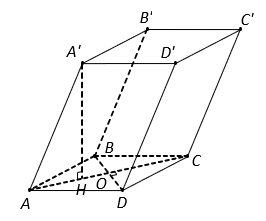
Từ giả thiết suy ra tam giác ABD đều cạnh .
Gọi H là tâm tam giác ABD. Vì A' cách đều các điểm A,B, D nên .
Do đó .
Ta có .
Tam giác vuông , có
.
Diện tích hình thoi .
Vậy .
Cho hình chóp đều ![]() có tất cả các cạnh bằng
có tất cả các cạnh bằng ![]() . Mặt phẳng
. Mặt phẳng ![]() song song với mặt đáy
song song với mặt đáy ![]() và cắt các cạnh bên
và cắt các cạnh bên ![]() lần lượt tại
lần lượt tại ![]() . Tính diện tích tam giác
. Tính diện tích tam giác ![]() biết mặt phẳng
biết mặt phẳng ![]() chia khối chóp đã cho thành hai phần có thể tích bằng nhau.
chia khối chóp đã cho thành hai phần có thể tích bằng nhau.
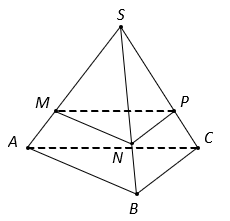
Mặt phẳng và cắt các cạnh
lần lượt tại
.
Theo Talet, ta có .
Do đó .
Theo giả thiết .
Suy ra tam giác MNP là tam giác đều cạnh .
Vậy diện tích .
Cho hình hộp chữ nhật ![]() có
có ![]() , đường chéo
, đường chéo ![]() hợp với mặt đáy
hợp với mặt đáy ![]() một góc
một góc ![]() thỏa mãn
thỏa mãn ![]() . Tính theo
. Tính theo ![]() thể tích khối hộp đã cho.
thể tích khối hộp đã cho.
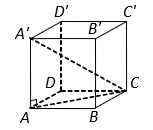
Ta có nên
.
Tam giác vuông , ta có
.
Tam giác vuông , ta có
.
Diện tích hình chữ nhật là
.
Vậy .
Cho hình lăng trụ tam giác ![]() có đáy
có đáy ![]() là tam giác vuông cân tại
là tam giác vuông cân tại ![]() , cạnh
, cạnh ![]() . Biết
. Biết ![]() tạo với mặt phẳng
tạo với mặt phẳng ![]() một góc
một góc ![]() và
và ![]() . Tính thể tích
. Tính thể tích ![]() của khối đa diện
của khối đa diện ![]() .
.
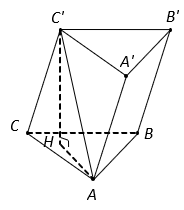
Gọi H là hình chiếu của C' trên mặt phẳng .
Suy ra AH là hình chiếu của AC' trên mặt phẳng .
Do đó
Tam giác vuông , có
Thể tích khối lăng trụ
Suy ra thể tích cần tính là:
.
Cho hình chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh
là hình vuông cạnh ![]() . Gọi
. Gọi ![]() và
và ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() và
và ![]() ;
; ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Biết
. Biết ![]() vuông góc với mặt phẳng
vuông góc với mặt phẳng ![]() và
và ![]() . Tính thể tích khối chóp
. Tính thể tích khối chóp ![]() .
.
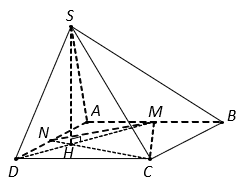
Theo giả thiết, ta có .
Diện tích tứ giác:
Vậy .
Cho lăng trụ đứng ![]() có đáy
có đáy ![]() là tam giác với
là tam giác với ![]() . Tính thể tích
. Tính thể tích ![]() của khối lăng trụ đã cho.
của khối lăng trụ đã cho.
Áp dụng công thức tính thể tích khối lăng trụ là:
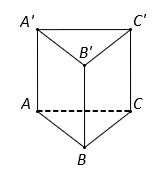
Diện tích tam giác là
.
Vậy thể tích khối lăng trụ
Cho lăng trụ ![]() có đáy
có đáy ![]() là hình chữ nhật tâm
là hình chữ nhật tâm ![]() và
và ![]() ;
; ![]() vuông góc với đáy
vuông góc với đáy ![]() . Cạnh bên
. Cạnh bên ![]() hợp với mặt đáy
hợp với mặt đáy ![]() một góc
một góc ![]() . Tính theo
. Tính theo ![]() thể tích
thể tích ![]() của khối lăng trụ đã cho.
của khối lăng trụ đã cho.
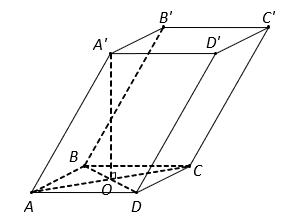
Vì nên
.
Đường chéo hình chữ nhật:
Suy ra tam giác vuông cân tại
nên
Diện tích hình chữ nhật .
Vậy .
Tính thể tích ![]() của khối lăng trụ tam giác đều có tất cả các cạnh bằng
của khối lăng trụ tam giác đều có tất cả các cạnh bằng ![]() ?
?
Áp dụng công thức tính thể tích khối lăng trụ là:

Xét khối lăng trụ tam giác đều có tất cả các cạnh bằng
.
Cho hình hộp chữ nhật có diện tích ba mặt cùng xuất phát từ cùng một đỉnh là ![]() . Tính thể tích
. Tính thể tích ![]() của hình hộp chữ nhật đã cho.
của hình hộp chữ nhật đã cho.
Áp dụng công thức tính thể tích khối lăng trụ là:

Xét hình hộp chữ nhật có đáy
là hình chữ nhật.
Theo bài ra, ta có
Nhân vế theo vế, ta được
Vậy .
Cho khối lăng trụ đứng ![]() có
có ![]() , đáy
, đáy ![]() là tam giác vuông cân tại
là tam giác vuông cân tại ![]() và
và ![]() . Tính thể tích của khối lăng trụ đã cho.
. Tính thể tích của khối lăng trụ đã cho.
Áp dụng công thức tính thể tích khối lăng trụ là:
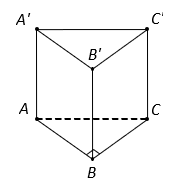
Tam giác vuông cân tại
,
suy ra
Vậy thể tích khối lăng trụ
Tính thể tích ![]() của khối lăng trụ
của khối lăng trụ ![]() biết thể tích khối chóp
biết thể tích khối chóp ![]() bằng
bằng ![]()
Ta có thể tích khối chóp:
Suy ra:
Cho khối chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh
là hình vuông cạnh ![]() ,
, ![]() vuông góc với đáy và khoảng cách từ
vuông góc với đáy và khoảng cách từ ![]() đến mặt phẳng
đến mặt phẳng ![]() bằng
bằng ![]() . Tính thể tích
. Tính thể tích ![]() của khối chóp đã cho.
của khối chóp đã cho.
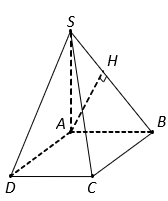
Gọi là hình chiếu của
trên
Ta có
Suy ra
Tam giác vuông tại
, có
Vậy .
Tính thể tích ![]() của một khối lăng trụ biết đáy có diện tích
của một khối lăng trụ biết đáy có diện tích ![]() , cạnh bên tạo với mặt phẳng đáy một góc
, cạnh bên tạo với mặt phẳng đáy một góc ![]() và độ dài cạnh bên bằng 10 cm.
và độ dài cạnh bên bằng 10 cm.
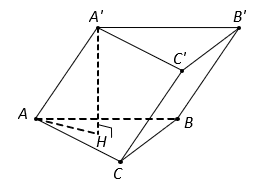
Xét khối lăng trụ có đáy là tam giác ABC.
Gọi H là hình chiếu của A' trên mặt phẳng
.
Suy ra là hình chiếu của
trên mặt phẳng
.
Do đó
Tam giác vuông tại H, có
.
Vậy .
Cho lăng trụ đứng ![]() có đáy
có đáy ![]() là tam giác vuông tại
là tam giác vuông tại ![]() và
và ![]() . Cạnh
. Cạnh ![]() tạo với mặt đáy
tạo với mặt đáy ![]() góc
góc ![]() . Tính thể tích
. Tính thể tích ![]() của khối lăng trụ đã cho.
của khối lăng trụ đã cho.
Áp dụng công thức tính thể tích khối lăng trụ là:
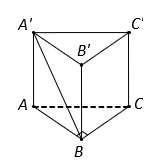
Vì là lăng trụ đứng nên
, suy ra hình chiếu vuông góc của
trên mặt đáy
là
.
Do đó .
Tam giác vuông , ta có
Diện tích tam giác là
Vậy .
Cho hình lăng trụ đứng ![]() có đáy là hình vuông cạnh
có đáy là hình vuông cạnh ![]() . Tính thể tích
. Tính thể tích ![]() của khối lăng trụ đã cho theo
của khối lăng trụ đã cho theo ![]() , biết
, biết ![]() .
.
Áp dụng công thức tính thể tích khối lăng trụ là:
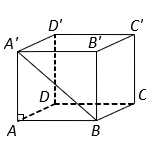
Do là lăng trụ đứng nên
.
Xét tam giác vuông , ta có
.
Diện tích hình vuông là
.
Vậy
Cho hình lăng trụ ![]() có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của
có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của ![]() lên mặt phẳng
lên mặt phẳng ![]() trùng với trung điểm
trùng với trung điểm ![]() của
của ![]() . Góc tạo bởi cạnh bên
. Góc tạo bởi cạnh bên ![]() với mặt đáy là
với mặt đáy là ![]() . Tính thể tích khối trụ
. Tính thể tích khối trụ ![]() .
.
3 || Ba || ba || V=3
Cho hình lăng trụ có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của
lên mặt phẳng
trùng với trung điểm
của
. Góc tạo bởi cạnh bên
với mặt đáy là
. Tính thể tích khối trụ
.
3 || Ba || ba || V=3
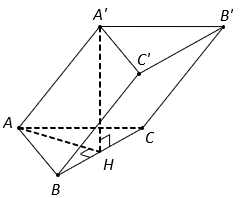
Tam giác đều ABC cạnh bằng 2 nên .
Vì nên hình chiếu vuông góc của
trên mặt đáy
là AH.
Do đó .
Suy ra tam giác vuông cân tại H nên
.
Diện tích tam giác đều ABC là .
Vậy .
Cho tứ diện ![]() có thể tích
có thể tích ![]() . Gọi
. Gọi ![]() là thể tích của khối tứ diện có các đỉnh là trọng tâm của các mặt của khối tứ diện
là thể tích của khối tứ diện có các đỉnh là trọng tâm của các mặt của khối tứ diện ![]() . Tính tỉ số
. Tính tỉ số ![]() .
.
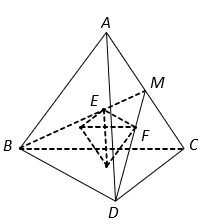
Gọi là trung điểm AC; E và F lần lượt là trọng tâm của tam giác ABC, ACD.
Trong tam giác MBD có .
Tương tự ta có các cạnh còn lại của tứ diện mới sinh ra bằng cạnh của tứ diện ban đầu.
Do đó .
Cho hình hộp chữ nhật có đường chéo ![]() . Độ dài ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân có công bội
. Độ dài ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân có công bội ![]() . Thể tích của khối hộp chữ nhật là?
. Thể tích của khối hộp chữ nhật là?
Áp dụng công thức tính thể tích khối hộp chữ nhật là:

Xét hình hộp chữ nhật có độ dài kích thước ba cạnh lần lượt là
và có đường chéo
.
Theo bài ra, ta có lập thành cấp số nhân có công bội
. Suy ra:
Mặt khác, độ dài đường chéo
Ta có hệ:
Vậy thể tích khối hộp chữ nhật là:
Cho tứ diện ![]() có thể tích bằng
có thể tích bằng ![]() và
và ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() . Tính thể tích
. Tính thể tích ![]() của khối chóp .
của khối chóp .![]()
4 || Bốn || bốn
Cho tứ diện có thể tích bằng
và
là trọng tâm của tam giác
. Tính thể tích
của khối chóp .
4 || Bốn || bốn
Vì là trọng tâm của tam giác
nên
.
Suy ra
