Lớp 12 Toán 12

Cực trị của hàm số

Bài học Lí thuyết toán 12: Cực trị của hàm số giới thiệu cho các em về khái niệm cực đại, cực tiểu của hàm số và quy tắc tìm cực trị của hàm số. Bên cạnh đó là một số ví dụ bài tập có lời giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia.

1. Khái niệm cực trị

Cho hàm số y=f(x) xác định và liên tục trên khoảng (a;b)  (có thể  a là - \infty; b là +\infty) và điểm x_0 \in (a;b).

  • Nếu tồn tại số h > 0 sao cho f\left( x \right) < f\left( {{x_0}} \right) với mọi x \in ({x_0} - h;{x_0} + h) và x \ne {x_0} thì ta nói hàm số f(x) đạt cực đại tại x_0.
  • Nếu tồn tại số h > 0 sao cho f\left( x \right) > f\left( {{x_0}} \right) với mọi x \in ({x_0} - h;{x_0} + h) và x \ne {x_0} thì ta nói hàm số f(x) đạt cực tiểu tại x_0.

2. Điều kiện để hàm số có cực trị

Giả sử hàm số y=f(x) liên tục trên K = ({x_0} - h;{x_0} + h) và có đạo hàm trên K  hoặc trên K\backslash {\text{\{ }}{x_0}{\text{\} }}, với h > 0.

  • Nếu f'\left( x \right) > 0 trên khoảng ({x_0} - h;{x_0}) và f'(x) < 0 trên ({x_0};{x_0} + h) thì x_0 là một điểm cực đại của hàm số f(x).
  • Nếu f'(x) < 0 trên khoảng ({x_0} - h;{x_0}) và f'\left( x \right) > 0 trên ({x_0};{x_0} + h) thì x_0 là một điểm cực tiểu của hàm số f(x).

Ta minh họa bằng Bảng biến thiên sau:

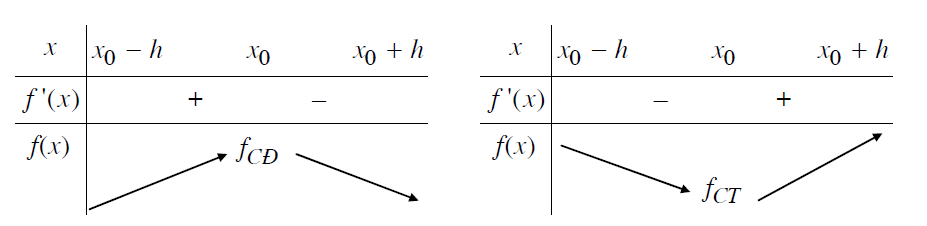
Minh họa bằng bảng biến thiên

Chú ý:

  • Nếu hàm số y=f(x) đạt cực đại (cực tiểu) tại x_0 thì được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x_0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là {f_{CĐ }}({f_{CT}}), còn điểm M({x_0};f({x_0})) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
  • Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

3. Quy tắc tìm cực trị

3.1. Quy tắc 1

  • Bước 1: Tìm tập xác định của hàm số.
  • Bước 2: Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
  • Bước 3: Lập bảng biến thiên.
  • Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.

3.2. Quy tắc 2

  • Bước 1: Tìm tập xác định của hàm số.
  • Bước 2: Tính f'(x). Giải phương trình f'(x) và ký hiệu x_i \,\, (i=1,2,3,...) là các nghiệm của nó.
  • Bước 3: Tính f''(x) và f''(x_i).
  • Bước 4: Dựa vào dấu của f''(x_i) suy ra tính chất cực trị của điểm x_i.

Ví dụ: Gọi M, n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số y = \frac{{{x^2} + 3x + 3}}{{x + 2}}.

Khi đó giá trị của biểu thức {M^2} - 2n bằng:

Giải:

+) Theo đề bài, ta có đạo hàm của hàm số là: y' = \frac{{{x^2} + 4x + 3}}{{{{(x + 2)}^2}}}

+) Xét: y' = 0 \Leftrightarrow \frac{{{x^2} + 4x + 3}}{{{{(x + 2)}^2}}} = 0 \Leftrightarrow \left[ \begin{gathered} x = - 3 \hfill \\ x = - 1 \hfill \\ \end{gathered} \right.

+) Suy ra:

  • Hàm số đạt cực đại tại x=-3 và y_{CĐ} =-3
  • Hàm số đạt cực tiểu tại x = -1 và y _{CT}=1

\Rightarrow {M^2} - 2n = 7

Vậy giá trị của biểu thức cần tìm là 7.

Câu trắc nghiệm mã số: 457,458,459,461,462,463,466,468
  • 76 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12