Lớp 12 Toán 12

Đề Ôn tập chương 4 (Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 30 câu
  • Điểm số bài kiểm tra: 30 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Tìm nghiệm

    Nghiệm của phương trình sau trên trường số phức là:z^4 – 4z^3 +7z^2 – 16z + 12 = 0

    Hướng dẫn:

    Do tổng tất cả các hệ số của phương trình bằng 0 nên pt có nghiệm z = 1.

    z^4 – 4z^3 +7z^2 – 16z + 12 = 0

    \Leftrightarrow (z – 1)(z^3 – 3z^2 + 4z – 12) = 0

    \Leftrightarrow (z – 1) (z – 3) (z^2 + 4) = 0

    \Leftrightarrow\left[ \begin{array}{l}z = 1\\z = 3\\{z^2} + 4 = 0\end{array} ight. \Leftrightarrow \left[ \begin{array}{l}z = 1\\z = 3\\z = 2i\\z = - 2i\end{array} ight.

    Vậy phương trình đã cho có 4 nghiệm:z = {m{\{ }}1;\,\,3;\,\,2i;\,\, - 2i{m{ \} }}.

  • Câu 2: Vận dụng cao
    Tìm giá trị lớn nhất của đoạn thẳng MN

    Gọi (C) là tập hợp các điểm trên mặt phẳng biểu diễn số phức z = x - 1 + yi,\left( {x,y \in \mathbb{R}} ight)

    thỏa mãn \left| z ight| = 1 và N là điểm biểu diễn số phức {z_0} = 5 + 3i. M là một điểm thuộc (C)

    sao cho MN có độ dài lớn nhất. Khi đó độ dài MN lớn nhất bằng

    Hướng dẫn:

    Ta có: M(x; y) nằm trên đường tròn (C): {\left( {x - 1} ight)^2} + {y^2} = 1. Tâm i(1; 0)

    Do N(5; 3) nằm ngoài (C)  nên MN có độ dài lớn nhất khi MN = NI + R = 5 + 1 = 6

  • Câu 3: Vận dụng cao
    Tìm GTLN của môđun số phức z

    Cho số phức z = \frac{{ - m + i}}{{1 - m(m - 2i)}},\,\,m \in \mathbb R. Tìm {\left| z ight|_{\max }}?

    Hướng dẫn:

     Ta có: z = \frac{{ - m + i}}{{1 - m(m - 2i)}} = \frac{m}{{{m^2} + 1}} + \frac{i}{{{m^2} + 1}}

    \Rightarrow \left| z ight| = \sqrt {\frac{1}{{{m^2} + 1}}} \le 1

    \Rightarrow {\left| z ight|_{\max }} = 1 \Leftrightarrow m = 0.

  • Câu 4: Vận dụng cao
    Tìm số phần tử

    Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z.\bar z = 1 và \left| {z - \sqrt 3 + i} ight| = m. Tìm số phần tử của S. 

    2 || Hai || hai

    Đáp án là:

    Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z.\bar z = 1 và \left| {z - \sqrt 3 + i} ight| = m. Tìm số phần tử của S. 

    2 || Hai || hai

    Điều kiện: m > 0.

    Đặt z = x + yi\left( {x,y \in \mathbb{R}} ight).

    Theo giả thiết z.\bar z = 1 \Leftrightarrow {\left| z ight|^2} = 1 \Leftrightarrow {x^2} + {y^2} = 1\left( {{C_1}} ight).

    \left( {{C_1}} ight) là đường tròn tâm O(0; 0), bán kính {R_1} = 1.

    Mặt khác  {R_1} = 1

    \left( {{C_2}} ight) là đường tròn tâm I\left( {\sqrt 3 ; - 1} ight), bán kính {R_2} = m.

    Để tồn tại duy nhất số phức z thì \left( {{C_1}} ight) và \left( {{C_2}} ight) tiếp xúc ngoài hoặc trong.

    TH1: \left( {{C_1}} ight) và \left( {{C_2}} ight) tiếp xúc ngoài khi và chỉ khi {R_1} + {R_2} = OI \Leftrightarrow 1 + m = 2 \Leftrightarrow m = 1\left( {TM} ight).

    TH2: \left( {{C_1}} ight) và \left( {{C_2}} ight) tiếp xúc trong khi và chỉ khi \left[ \begin{array}{l}{R_1} + OI = {R_2} \Leftrightarrow 1 + 2 = m \Leftrightarrow m = 3\,\,\,\,\,\,\left( {TM} ight)\\OI + {R_2} = {R_1} \Leftrightarrow m + 2 = 1 \Leftrightarrow m = - 1\,\,\,\,\,\,(L)\end{array} ight..

    Vậy S = \left\{ {1,3} ight\}.

  • Câu 5: Thông hiểu
    Tính giá trị x và y thỏa mãn điều kiện

    Cho {\left( {x + 2i} ight)^2} = 3x + yi,\left( {x,y \in \mathbb{R}} ight). Giá trị của x và y bằng:

    Hướng dẫn:

     Ta có:

    {\left( {x + 2i} ight)^2} = 3x + yi \Leftrightarrow {x^2} - 4 + 4xi = 3x + yi

    \Leftrightarrow \left\{ \begin{gathered} {x^2} - 4 = 3x \hfill \\ 4x = y \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} x = - 1 \hfill \\ x = 4 \hfill \\ \end{gathered} ight. \hfill \\ 4x = y \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x = - 1 \hfill \\ y = - 4 \hfill \\ \end{gathered} ight. \hfill \\ \left\{ \begin{gathered} x = 4 \hfill \\ y = 16 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight.

  • Câu 6: Vận dụng cao
    Tính mô đun của số phức w

    Cho số phức z thỏa mãn \left| {z - 3 - 4i} ight| = \sqrt 5. Gọi M, n lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = {\left| {z + 2} ight|^2} - {\left| {z - i} ight|^2}. Khi đó mô đun của số phức {\text{w}} = M + mi

    Hướng dẫn:

     Giả sử z = x + yi\left( {x,y \in R} ight) ta có:

    \left| {z - 3 - 4i} ight| = \sqrt 5

    \Leftrightarrow {\left( {x - 3} ight)^2} + {\left( {y - 4} ight)^2} = 5

    Ta có

    P = 4x + 2y + 3 \Leftrightarrow 4\left( {x - 3} ight) + 2\left( {y - 4} ight) = P - 23

    Ta có

    {\left[ {4\left( {x - 3} ight) + 2\left( {y - 4} ight)} ight]^2} \leqslant 20\left[ {{{\left( {x - 3} ight)}^2} + {{\left( {y - 4} ight)}^2}} ight] = 100

    => - 10 \leqslant P - 23 \leqslant 10

    \Leftrightarrow 13 \leqslant P \leqslant 33

    => M = 33,m = 13

    Ta thu được kết quả: w = 33 + 13i

    => \left| {\text{w}} ight| = \sqrt {1258}

     

  • Câu 7: Vận dụng
    Chọn phương án đúng nhất

    Cho hai điểm A, B là hai điểm biểu diễn hình học số phức theo thứ tự z_0, z_1, khác 0 và

    thỏa mãn đẳng thức z_0^2+z_1^2=z_0z_1. Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ) ? Chọn phương án đúng và đầy đủ nhất.

    Hướng dẫn:

    Hai điểm A, B là hai điểm biểu diễn hình học số phức theo thứ tự z_0, z_1.

    Theo giả thiết suy ra: OA=|z_0|, OB=|z_1| và AB=|z_1-z_0|.

    Ta có: z_0^2+z_1^2=z_0z_1 \Leftrightarrow z_0^2-z_0z_1+z_1^2=0.

    \Leftrightarrow (z_0 +z_1)(z_0^2-z_0z_1+z_1^2)=0

    \Leftrightarrow z_0^3+z_1^3=0 \Leftrightarrow z_0^3=-z_1^2\Leftrightarrow |z_0|=|z_1| \Leftrightarrow OA=OB

    Xét (z_1-z_0)^2=z_0^2+z_1^2-2z_0z_1=-z_0z_1 \Rightarrow |z_1-z_0|^2=|z_1|.|z_0|

    \Leftrightarrow AB^2=OA.OB \Leftrightarrow AB=OB.

    Vậy OA=OB=AB hay tam giác OAB là tam giác đều.

  • Câu 8: Thông hiểu
    Tìm x, y thỏa mãn điều kiện

    Tìm các số thực x, y thoả mãn:

    3x + y + 5xi = 2y – 1 +(x – y)i

    Hướng dẫn:

    Theo giả thiết: 3x + y + 5xi = 2y – 1 +(x – y)i

    => (3x + y) + (5x)i = (2y – 1) +(x – y)i

    =>\left\{ \begin{gathered} 3x + y = 2y - 1 \hfill \\ 5x = x - y \hfill \\ \end{gathered} ight.

    => \left\{ \begin{gathered} x = - \frac{1}{7} \hfill \\ y = \frac{4}{7} \hfill \\ \end{gathered} ight.

  • Câu 9: Nhận biết
    Số phức liên hợp của số phức

    Số phức liên hợp của số phức 5 - 3i là

    Gợi ý:

     Cho số phức z = a + bi. Số phức \overline z = a – bi gọi là số phức liên hợp với số phức trên hay \overline z = \overline {a + bi} = a - bi

    Hướng dẫn:

    \overline z = \overline {a + bi} = a – bi

    \Rightarrow \overline z = \overline {5 - 3i} = 5 - ( - 3i) = 5 + 3i

  • Câu 10: Nhận biết
    Số phức liên hợp của số phức 3 - 2i

    Số phức liên hợp của số phức 3 - 2i là

    Gợi ý:

     Cho số phức z = a + bi. Số phức \overline z = a – bi gọi là số phức liên hợp với số phức trên hay \overline z = \overline {a + bi} = a - bi

    Hướng dẫn:

     \overline z = \overline {a + bi} = a – bi

    \Rightarrow \overline z = \overline {3 - 2i} = 3 - ( - 2i) = 3 + 2i

  • Câu 11: Vận dụng cao
    Giá trị lớn nhất của biểu thức

    Cho số phức z thỏa mãn điêu kiện \left| {z - 1} ight| = \sqrt 2. Tính giá trị lớn nhất của biểu thức T = \left| {z + i} ight| + \left| {z - 2 - i} ight|

    Hướng dẫn:

    Đặt z = x + yi\left( {x,y \in \mathbb{R}} ight), ta có:

    \left| {z - 1} ight| = \sqrt 2 \Leftrightarrow \left| {x - 1 + yi} ight| = \sqrt 2

    \Leftrightarrow {\left( {x - 1} ight)^2} + {y^2} = 2 \Leftrightarrow {x^2} + {y^2} = 2x + 1\left( * ight)

    Mặt khác: T = \left| {z + i} ight| + \left| {z - 2 - i} ight| = \left| {x + \left( {y + 1} ight)i} ight| + \left| {x - 2} ight| + \left( {y - 1} ight)i

    = \sqrt {{x^2} + {{\left( {y + 1} ight)}^2}} + \sqrt {{{\left( {x - 2} ight)}^2} + {{\left( {y - 1} ight)}^2}}

    = \sqrt {{x^2} + {y^2} + 2y + 1} + \sqrt {{x^2} + {y^2} - 4x - 2y + 5}

    Kết hợp với (*), ta được:

    T = \sqrt {2x + 2y + 2} + \sqrt {6 - 2x - 2y}

    Áp dụng bất đẳng thức Bunhacopxki ta được

    T \leqslant \sqrt {\left( {{1^2} + {1^2}} ight)\left[ {{{\left( {\sqrt {2x + 2y + 2} } ight)}^2} + {{\left( {\sqrt {6 - 2x - 2y} } ight)}^2}} ight]} = 4

    Vậy \max T = 4

  • Câu 12: Thông hiểu
    Xác định số phức

    Số phức z thỏa mãn: \left( {1 + i} ight)z + \left( {2 - 3i} ight)\left( {1 + 2i} ight) = 7 + 3i là:

    Hướng dẫn:

     Ta áp dụng các quy tắc thực hiện phép tính, có:

    \begin{matrix} \left( {1 + i} ight)z + \left( {2 - 3i} ight)\left( {1 + 2i} ight) = 7 + 3i \hfill \\ \Leftrightarrow (1 + i)z = 7 + 3i - (2 - 3i)(1 + 2i) \hfill \\ \Leftrightarrow (1 + i)z = - 1 + 2i \hfill \\ \Leftrightarrow z = \dfrac{{ - 1 + 2i}}{{1 + i}} \hfill \\ \Leftrightarrow z = \dfrac{1}{2} + \dfrac{3}{2}i \hfill \\ \end{matrix}

    Ngoài ra ta có thể sử dụng lệnh CALC trong máy tính để thử các phương án.

  • Câu 13: Vận dụng cao
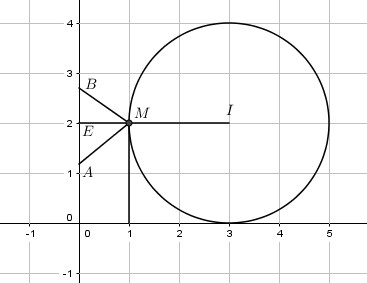
    Tìm giá trị nhỏ nhất của biểu thức

    Gọi {z_1},{z_2} là 2 nghiệm của phương trình \left| {z - 1 + 2i} ight| = \left| {z + 1 + 2i} ight| thỏa mãn \left| {{z_1} - {z_2}} ight| = \sqrt 2. Biết rằng w là số phức thỏa mãn \left| {{\text{w}} - 3 - 2i} ight| = 2. Tìm GTNN của biểu thức P = \left| {{\text{w}} - {z_1}} ight| + \left| {{\text{w}} - {z_2}} ight|.

    Hướng dẫn:

    Giả sử z = x yi\left( {x,y \in R} ight)

    Ta có: \left| {z - 1 + 2i} ight| = \left| {z + 1 + 2i} ight|

    => x = 0

    => Tập hợp điểm biểu diễn {z_1},{z_2} là trục tung.

    Giả sử A, B lần lượt là 2 điểm biểu diễn cho {z_1},{z_2}, ta có \left| {{z_1} - {z_2}} ight| = \sqrt 2 \Leftrightarrow AB = \sqrt 2

    Giả sử {\text{w}} = a + bi\left( {a,b \in R} ight) và M là điểm biểu diễn cho số phức w, ta có \left| {{\text{w}} - 3 - 2i} ight| = 2 \Leftrightarrow {(a - 3)^2} + {(b - 2)^2} = 4a suy ra tập hợp điểm biểu diễn M cho số phức w là đường tròn tâm I\left( {3;2} ight) bán kính R = 2

    Ta có P = MA + MB, gọi E là hình chiếu vuông góc của I lên trục tung, ta thấy P nhỏ nhất khi E là trung điểm AB suy ra MA = MB = \frac{{\sqrt 6 }}{2}, vậy MinP = 2.\frac{{\sqrt 6 }}{2} = \sqrt 6

    Tìm giá trị nhỏ nhất của biểu thức

  • Câu 14: Nhận biết
    Tìm số phức thỏa mãn điều kiện

    Số phức có phần thực bằng 1 và phần ảo bằng 3 là

    Gợi ý:

     Áp dụng áp dụng định nghĩa số phức có dạng z = a + bi (trong đó a, b là các số thực và số i thoả mãn i2 = -1).

    Hướng dẫn:

     Số phức z = a + bi có a được gọi là phần ảo, b là phần thực.

  • Câu 15: Vận dụng
    Tính giá trị biểu thức M

    Cho biểu thức M = 1 - z + {z^2} - {z^3} + ... + {z^{2016}} - {z^{2017}} với z = \frac{{1 + 2i}}{{2 - i}}. Biểu thức M có giá tri là?

    Hướng dẫn:

    Ta có: z = \frac{{1 + 2i}}{{2 - i}} = i.

    Khi đó:  M = \frac{{1 - {{( - z)}^{2018}}}}{{1 + z}} = \frac{{1 - {z^{2018}}}}{{1 + z}}

    = \frac{{1 - {z^{2018}}}}{{1 + z}} = \frac{{1 - {i^{2018}}}}{{1 + i}} = 1 - i.

  • Câu 16: Vận dụng cao
    Điều kiện để đoạn thẳng MN đạt min

    Gọi (C) là tập hợp các điểm trên mặt phẳng biểu diễn số phức z = x - 1 + yi;\left( {x,y \in \mathbb{R}} ight)

    thỏa mãn \left| z ight| = 1 và N là điểm biểu diễn số phức {z_0} = 5 + 3i. M là một điểm thuộc (C)

    sao cho MN có độ dài bé nhất. Khi đó độ dài MN bé nhất bằng

    Hướng dẫn:

    Ta có: M(x; y) nằm trên đường tròn (C). Tâm I(1; 0)

    Do N(5, 3) nằm ngoài (C) nên MN có độ dài bé nhất khi MN = NI - R = 5 - 1 = 4

  • Câu 17: Thông hiểu
    Căn bậc hai của số phức

    Tìm các căn bậc hai của số phức z = 5 + 12i

    Hướng dẫn:

     Giả sử m + ni (m; n \in R) là căn bậc hai của z

    Ta có: {(m + ni)^2} = 5 + 12i

    \Leftrightarrow {m^2} + 2mni + {n^2}{i^2} = 5 + 12i \Leftrightarrow {m^2} + 2mni - {n^2} = 5 + 12i

    \Leftrightarrow \left\{ \begin{gathered} {m^2} - {n^2} = 5 \hfill \\ 2mn = 12 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} {m^2} - {n^2} = 5(1) \hfill \\ m = \frac{6}{n}(2) \hfill \\ \end{gathered} ight.

    Thay (2) vào (1) ta có: {\left( {\frac{6}{n}} ight)^2} - {n^2} = 5 \Leftrightarrow 36 - {n^4} = 5{n^2}

    \Leftrightarrow {n^4} + 5{n^2} - 36 = 0 \Leftrightarrow {n^2} = 4;{n^2} = - 9(loai)

    \left[ \begin{gathered} n = 2 \Rightarrow m = 3 \hfill \\ n = - 2 \Rightarrow m = - 3 \hfill \\ \end{gathered} ight.

    Vậy z có hai căn bậc hai là 3+2i và -3-2i.

  • Câu 18: Vận dụng
    Tìm điều kiện

    Cho hai số thực b và c (c>0). Kí hiệu A , B là hai điểm biểu diễn hai nghiệm phức của phương trình {z^2} + 2bz + c = 0 trong mặt phẳng phức. Tìm điều kiện của b và c để tam giác OAB là tam giác vuông (O là gốc tọa độ).

    Hướng dẫn:

     Ta có: {z^2} + 2bz + c = 0 . Vì {z_1} + {z_2} = - 2b và {z_1}{z_2} = c là số thực.

    \Rightarrow {z_2} = \overline {{z_1}} \Rightarrow \left| {{z_2}} ight| = \left| {\overline {{z_1}} } ight| = \left| {{z_1}} ight|. Vậy ta có: {x_1} = b và x_1^2 + y_2^2 = c .

    Ta có: {z_1} = {x_1} + {y_1}i \Rightarrow A\left( {{x_1};{y_1}} ight); {z_1} = {x_2} + {y_2}i \Rightarrow B(x_2;y_2).

    Để tam giác OAB là tam giác vuông tại O = > \overrightarrow {OA} .\overrightarrow {OB} = 0

    \Rightarrow {x_1}{x_2} + {y_1}{y_2} = 0\Rightarrow x_1^2-y_1^2=0\Rightarrow x_1^2=y_1^2\Rightarrow c=2b^2.

  • Câu 19: Nhận biết
    Giá trị của số phức z

    Cho số phức z = 1 + 2i, giá trị của số phức w = z + i\overline z là?

    Hướng dẫn:

    Ta có: w = z + i\overline z = \left( {1 + 2i} ight) + i\left( {1 - 2i} ight) = 3 + 3i

  • Câu 20: Thông hiểu
    Số nghiệm của phương trình

    Số nghiệm của phương trình: (z^2 + 3z +6)^2 + 2z(z^2 + 3z +6) – 3z^2 = 0 là?

    Hướng dẫn:

     Đặt t = z^2 + 3z +6 phương trình đã cho có dang:

    t^2 +2zt – 3z^2 = 0 \Leftrightarrow (t – z)(t+3z) = 0 \Leftrightarrow\left[ \begin{array}{l}t = z\\t = - 3z\end{array} ight.

    + Với t = z \Leftrightarrow z^2 + 3z +6 –z = 0 \Leftrightarrow z^2 + 2z + 6 = 0 \Leftrightarrow\left[ \begin{array}{l}z = - 1 + \sqrt 5 i\\z = - 1 - \sqrt 5 i\end{array} ight.

    + Với t = -3z \Leftrightarrow z^2 + 3z +6 +3z = 0 \Leftrightarrow z^2 + 6z + 6 = 0 \Leftrightarrow\left[ \begin{array}{l}z = - 3 + \sqrt 3 \\z = - 3 - \sqrt 3 \end{array} ight.

    Vậy phương trình đã cho có 4 nghiệm.

  • Câu 21: Nhận biết
    Nghiệm của PT bậc 3

    Phương trình {z^3} + 4{z^2} + (4 + i)z + 3 + 3i = 0 có tập nghiệm là:

    Hướng dẫn:

    Dễ thấy z=-i  là nghiệm của {z^3} + 4{z^2} + (4 + i)z + 3 + 3i = 0

    Nên {z^3} + 4{z^2} + (4 + i)z + 3 + 3i = 0 \Leftrightarrow \,(z + i)({z^2} + (4 - i)z + 3 - 3i) = 0

    \Leftrightarrow \left[ \begin{array}{l}z + i = 0\\{z^2} + (4 - i)z + 3 - 3i = 0\,\,\,(*)\end{array} ight.

    Giải (*), ta được:

    \Delta = {(4 - i)^2} - 12 + 12i = 16 - 1 - 8i - 12 + 12i

    = 3 + 4i = 4 + 2.2.i + {i^2} = {(2 + i)^2}

    Vậy có hai căn bậc hai là: 2+i và -2-i

    Do đó nghiệm của pt là \left[ \begin{array}{l}z = \dfrac{{ - 4 + i + 2 + i}}{2} = - 1 + i\\z = \dfrac{{ - 4 + i - 2 - i - 2}}{2} = - 3\end{array} ight.

    Vậy PT có 3 nghiệm là –i, -3, -1+i.

  • Câu 22: Vận dụng
    Có bao nhiêu tham số m thảo mãn?

    Cho số phức z = {\left( {\frac{{4i}}{{i + 1}}} ight)^m}, m nguyên dương. Có bao nhiêu giá trị m \in \left[ {1;100} ight] để z là số thực?

    Hướng dẫn:

    Ta có: z = {\left( {\frac{{4i}}{{i + 1}}} ight)^m} = {(8i)^{\frac{m}{2}}} = {8^{\frac{m}{2}}}.{i^{\frac{m}{2}}}

    z là số thực khi và chỉ khi \frac{m}{2} = 2k \Leftrightarrow m = 4k,\,\,k \in \mathbb N

    Vậy có 25 giá trị m thỏa yêu cầu đề bài.

  • Câu 23: Vận dụng cao
    Tìm phần ảo

    Biết {z_1},{z_2} = 5 - 4i và {z_3} là ba nghiệm của phương trình {z^3} + b{z^2} + cz + d = 0\,\,\,\left( {b,c,d \in \mathbb R} ight),

    trong đó {z_3} là nghiệm có phần ảo dương. Phần ảo của số phức w = {z_1} + 3{z_2} + 2\,{z_3} bằng:

    Hướng dẫn:

     Xét phương trình {z^3} + b{z^2} + cz + d = 0\,\,\,\left( {b,c,d \in \mathbb R} ight) là phương trình bậc ba với hệ số thực nên luôn có một nghiệm thực là z_1.

    Do đó phương trình tương đương với:

    \left( {z - {z_1}} ight)\left( {{z^2} + a'z + b'} ight) = 0\,\,\,\left( {a',b' \in \mathbb R} ight)

    \Leftrightarrow \left[ \begin{array}{l}z = {z_1}\,\, \in \mathbb R\\{z^2} + a'z + b' = 0\,\,\,\left( 1 ight)\end{array} ight..

    Nên {z_3},{z_2} = 5 - 4i là hai nghiệm phức của phương trình bậc hai với hệ số thực (1).

    Suy ra .{z_3} = 5 + 4i

    Khi đó : w = {z_1} + 3{z_2} + 2\,{z_3} = {z_1} + 3.\left( {5 - 4i} ight) + 2.\left( {5 + 4i} ight) = \left( {25 + 2{z_3}} ight) - 4i.

    Vậy phần ảo của w = {z_1} + 3{z_2} + 2\,{z_3} là -4.

  • Câu 24: Vận dụng
    Tìm số phức z thỏa mãn điều kiện

    Cho z1 = 1 + i; z2 = -1 - i. Tìm {z_3} \in \mathbb{C} sao cho các điểm biểu diễn của {z_1};\,\,{z_2};\,\,{z_3} tạo thành tam giác đều.

    Hướng dẫn:

     Giả sử {z_3} = x + yi

    Để các điểm biểu diễn của {z_1};\,\,{z_2};\,\,{z_3} tạo thành một tam giác đều thì

    \left\{ {\begin{array}{*{20}{c}} {\left| {{z_1} - {z_2}} ight| = \left| {{z_1} - {z_3}} ight|} \\ {\left| {{z_1} - {z_2}} ight| = \left| {{z_2} - {z_3}} ight|} \end{array}} ight.

    \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\sqrt {4 + 4} = \sqrt {{{\left( {x - 1} ight)}^2} + {{\left( {y - 1} ight)}^2}} } \\ {\sqrt {4 + 4} = \sqrt {{{\left( {x + 1} ight)}^2} + {{\left( {y + 1} ight)}^2}} } \end{array}} ight.

    \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{{\left( {x - 1} ight)}^2} + {{\left( {y - 1} ight)}^2} = 8} \\ {x + y = 0} \end{array}} ight.

    \Rightarrow 2{y^2} = 6 \Rightarrow y = \pm \sqrt 3 \Rightarrow x = \mp \sqrt 3

    Vậy có hai số phức thoả mãn là: {z_3} = {\text{\{ }}\sqrt 3 - \sqrt 3 i;\,\, - \sqrt 3 + \sqrt 3 i\}

  • Câu 25: Thông hiểu
    Tính tổng tất cả các nghiệm

    Tính tổng tất cả các nghiệm của phương trình sau: (z^2 + z)^2 + 4(z^2 + z) -12 = 0 là?

    Hướng dẫn:

     Đặt t = z^2 + z, khi đó phương trình đã cho có dạng:

    t^2 + 4t – 12 = 0 \Leftrightarrow\left[ \begin{array}{l}t = - 6\\t = 2\end{array} ight.

    \Leftrightarrow \left[ \begin{array}{l}{z^2} + z - 6 = 0\\{z^2} + z - 2 = 0\end{array} ight.

    \Leftrightarrow \left[ \begin{array}{l}z = \dfrac{{ - 1 + \sqrt {23} i}}{2}\\z = \dfrac{{ - 1 - \sqrt {23} i}}{2}\\z = 1\\z = - 2\end{array} ight.

    Vậy phương trình đã cho có 4 nghiệm có tổng là

    \frac{{ - 1 + \sqrt {23} i}}{2} + \frac{{ - 1 - \sqrt {23} i}}{2} + 1 - 2 = - 1 + 1 - 2 = - 2

  • Câu 26: Vận dụng cao
    Tìm dạng đại số của w

    Cho {z_1} = 1 + \sqrt 3 i; {z_2} = \frac{{7 + i}}{{4 - 3i}}; {z_3} = {\left( {1 - i} ight)^{2016}}. Tìm dạng đại số của w = z_1^{25}.z_2^{10}.z_3^{2016}.

    Hướng dẫn:

     Ta có:

    \left. \begin{array}{l}z_1^{25} = {(1 + \sqrt 3 i)^{25}} = {8^8} + {8^8}\sqrt 3 i\\z_2^{10} = {\left( {\frac{{7 + i}}{{4 - 3i}}} ight)^{10}} = {(2i)^5} = {2^5}i\\z_3^{2016} = {(1 - i)^{2016}} = {( - 2i)^{1008}} = {2^{1008}}\end{array} ight\}

    \Rightarrow w = z_1^{25}.z_2^{10}.z_3^{2016} = - {2^{1037}}\sqrt 3 + {2^{1037}}i.

  • Câu 27: Thông hiểu
    Tìm phần ảo của số phức

    Cho số phức z = a + bi. Số phức {z^2} có phần ảo là:

    Hướng dẫn:

    Ta có: {z^2} = {\left( {a + bi} ight)^2} = {a^2} - {b^2} + 2abi

  • Câu 28: Vận dụng
    Biểu diễn số phức z

    Điểm biểu diễn của số phức z = \frac{1}{{2 - 3i}} là:

    Hướng dẫn:

     Ta có: z = \frac{1}{{2 - 3i}} = \frac{2}{{13}} + \frac{3}{{13}}i

  • Câu 29: Nhận biết
    Tính giá trị biểu thức

    Giá trị của z = 1 + i + {i^2} + ... + {i^{2023}} là?

    Hướng dẫn:

    Ta có: z = \frac{{{i^{2022}} - 1}}{{i - 1}} = 1 + i

    (Áp dụng công thức: {S_n} = 1 + p + {p^2} + ... + {p^n} = \frac{{{p^{n - 1}} - 1}}{{p - 1}})

  • Câu 30: Thông hiểu
    Điểm biểu diễn của số phức

    Kí hiệu z_0 là nghiệm phức có phần ảo dương của phương trình 4{z^2} - 16z + 17 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w = i{z_0}?

    Hướng dẫn:

     Ta có:

    4{z^2} - 16z + 17 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_0} = 2 + \dfrac{1}{2}i\\z = 2 - \dfrac{1}{2}i\end{array} ight.

    \Rightarrow w = i{z_0} = - \frac{1}{2} + 2i

0/30
30 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (23%):
    2/3
  • Thông hiểu (27%):
    2/3
  • Vận dụng (20%):
    2/3
  • Vận dụng cao (30%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 1 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập