Số giá trị nguyên của tham số m để hàm số ![]() đồng biến trên
đồng biến trên ![]() ?
?
Ta có:
Hàm số đồng biến trên khi và chỉ khi
Kết hợp với điều kiện
Vậy có tất cả 5 giá trị của m thỏa mãn điều kiện đề bài.
Số giá trị nguyên của tham số m để hàm số ![]() đồng biến trên
đồng biến trên ![]() ?
?
Ta có:
Hàm số đồng biến trên khi và chỉ khi
Kết hợp với điều kiện
Vậy có tất cả 5 giá trị của m thỏa mãn điều kiện đề bài.
Giá trị của tham số m sao cho hàm số ![]() nghịch biến trên khoảng (0; 2)?
nghịch biến trên khoảng (0; 2)?
Ta có:
Hàm số nghịch biến trên khoảng (0; 2)
=>
=>
Xét hàm số
Ta có:
=> g(x) đồng biến trên đoạn [0; 2]
Ta có:
Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng
Ta có y’ = 8x => y’ = 0 => x = 0
=> y’ > 0 => x > 0
=> y’ < 0 => x < 0
Vậy hàm số đồng biến trên khoảng
Số giá trị nguyên của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên
đồng biến trên ![]() là:
là:
Ta có:
Hàm số đồng biến trên khi và chỉ khi
Kết hợp với điều kiện
=> Có 20 giá trị của tham số m thỏa mãn điều kiện đề bài.
Trong các hàm số sau, hàm số nào vừa có khoảng đồng biến vừa có khoảng nghịch biến trên tập xác định của nó. (I) ![]() ; (II)
; (II) ![]() ; (III)
; (III)
(I) Tập xác định
=> (I) không thỏa mãn
(II) Tập xác định
Bảng xét dấu
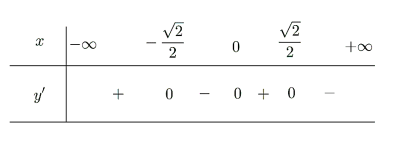
=> (II) thỏa mãn
(III) Tập xác định
=> Hàm số nghịch biến trên tập số thực
=> (III) không thỏa mãn
Gọi P là tập hợp các giá trị nguyên của tham số m để hàm số ![]() đồng biến trên tập xác định của nó. Tổng các phần tử của tập hợp P là:
đồng biến trên tập xác định của nó. Tổng các phần tử của tập hợp P là:
Ta có:
Hàm số đồng biến trên khi và chỉ khi
Kết hợp với điều kiện
=>
=> Tổng P bằng 10
Cho hàm số ![]() . Xác định tất cả các giá trị của tham số m để hàm số đã cho nghịch biến trong khoảng (0; +∞)
. Xác định tất cả các giá trị của tham số m để hàm số đã cho nghịch biến trong khoảng (0; +∞)
Ta có:
Hàm số đã cho nghịch biến trên khoảng (0; +∞)
=>
=>
=>
Xét ta có:
Ta lại có:
Cho hàm số y = f(x) có đạo hàm ![]() . Khi đó hàm số
. Khi đó hàm số ![]() nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
Ta có:
Ta có bảng xét dấu như sau:
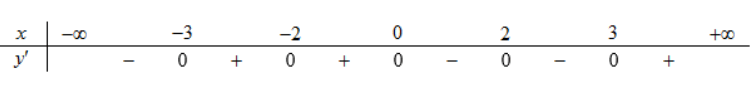
Dựa vào bảng xét dấu, hàm số nghịch biến trên các khoảng (-∞; -3) và (-0; 3)
Cho f(x) mà đồ thị hàm số y = f’(x) như hình vẽ.
Hàm số ![]() đồng biến trên khoảng nào trong các đáp án dưới đây?
đồng biến trên khoảng nào trong các đáp án dưới đây?
Ta có:
=>
Hàm số đồng biến khi
Đặt t = x – 1 thì (*) trở thành
Quan sát đồ thị hàm số y = f’(t) và y = -2t trên cùng một hệ tọa độ như hình vẽ
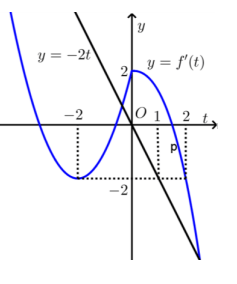
Khi đó ta thấy với thì độ thì hàm số y = f’(t) luôn nằm trên đường thẳng y = -2t
=>
Do đó với thì hàm số
đồng biến.
Cho hàm số ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Tập xác định của hàm số là:
Ta có:
Vậy hàm số đồng biến trên khoảng (5; +∞)
Trong các hàm số sau, hàm số nào nghịch biến trên tập xác định của nó?
Hàm trùng phương không nghịch biến trên tập xác định của nó
Với
Hàm số đã cho đồng biến trên từng khoảng xác định
Với
=> Hàm số nghịch biến trên
Cho hàm số ![]() . Mệnh đề nào dưới dây là đúng?
. Mệnh đề nào dưới dây là đúng?
Tập xác định của hàm số
Ta có:
Hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)
Cho hàm số ![]()
Ta có: có hai nghiệm phân biệt là -2 và 3
=> f’(x) < 0 =>
Vậy hàm số nghịch biến trên khoảng (-2; 3)
Tìm tất cả các khoảng đồng biến của hàm số ![]()
Tập xác định
Ta có:
=> Hàm số đồng biến trên (-3; 0)
Hàm số nào sau đây đồng biến trên ![]() ?
?
Hàm số có
Hàm số nào sau đây nghịch biến trên khoảng (1; 3)?
Xét hàm số có
=> y’ = 0 =>
Ta có bảng biến thiên như sau:
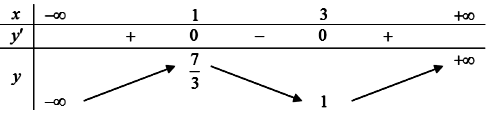
Do đó hàm số nghịch biến trên khoảng (1; 3)
Cho hàm số ![]() . Khẳng định nào dưới đây là khẳng định đúng?
. Khẳng định nào dưới đây là khẳng định đúng?
Hàm số có tập xác định
và có đạo hàm
=> A là khẳng định đúng
Trong các hàm số sau đây, hàm số nào không nghịch biến trên ![]() ?
?
Với
y’ > 0 khi x > 0 và y’ < 0 khi x < 0 nên hàm số không nghịch biến trên
Cho hàm số y = f(x) có đạo hàm f’(x) = x2 + 1, ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
Ta có:
f’(x) = x2 + 1 > 0,
=> Hàm số đống biến trên khoảng (-∞; +∞)
Trong các hàm số sau, hàm số nào đồng biến trên ![]() ?
?
Ta có:
Ta có: y’ = 0 chỉ tại x = 1
Vậy đồng biến trên
