Lớp 12 Toán 12

Đề Ôn tập chương 2: Mặt nón, mặt trụ, mặt cầu (Trung bình)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 30 câu
  • Điểm số bài kiểm tra: 30 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Tìm bán kính mặt cầu

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và BA = BC = a. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC  là:

    Hướng dẫn:

     Tìm bán kính

    Gọi M là trung điểm AC, suy ra M là tâm đường tròn ngoại tiếp tam giác ABC.

    Gọi I là trung điểm SC, suy ra IM ||SA nên IM \bot \left( {ABC} ight) .

    Do đó IM là trục của \triangle ABC, suy ra IA=IB=IC     (1)

    Hơn nữa, tam giác SAC vuông tại A có I là trung điểm SC nên IS=IC=IA.  (2)

    Từ (1) và (2) , ta có IS=IA=IB=IC

    hay I là tâm của mặt cầu ngoại tiếp hình chóp S.ABC.

    Vậy bán kính R = IS = \frac{{SC}}{2} = \frac{{\sqrt {S{A^2} + A{C^2}} }}{2} = \frac{{a\sqrt 6 }}{2} .

  • Câu 2: Thông hiểu
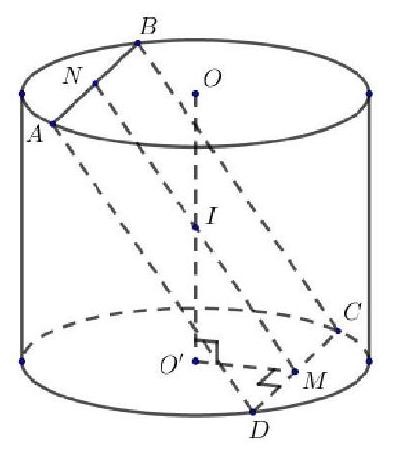
    Tính thể tích khối trụ

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chu vi đáy bằng 2a thì thể tích của nó bằng:

    Hướng dẫn:

     Gọi bán kính đáy là R.

    Hình trụ có chu vi đáy bằng 2a nên ta có 2\pi R = 2a \Leftrightarrow R = \frac{a}{\pi }.

    Suy ra hình trụ này có đường cao h=a.

    Vậy thể tích khối trụ V = \pi {R^2}h = \pi {\left( {\frac{a}{\pi }} ight)^2}a = \frac{{{a^3}}}{\pi }(đvtt).

  • Câu 3: Vận dụng
    Diện tích của thiết diện

    Một hình nón có bán kính đáy R, góc ở đỉnh là 60^0. Một thiết diện qua đỉnh nón chắn trên đáy một cung có số đo 90^0 . Diện tích của thiết diện là:

    Hướng dẫn:

     Diện tích của thiết diện

    Vì góc ở đỉnh là 60^0nên thiết diện qua trục SAC là tam giác đều cạnh 2R.

    Suy ra đường cao của hình nón là SI = R\sqrt 3.

    Tam giác SAB là thiết diện qua đỉnh, chắn trên đáy cung AB có số đo bằng 90^0 nên IAB là tam giác vuông cân tại I, suy ra AB = R\sqrt 2.

    Gọi M là trung điểm của AB thì \left\{ \begin{array}{l}IM \bot AB\\SM \bot AB\end{array} ight. và IM = \frac{{R\sqrt 2 }}{2}.

    Trong tam giác vuông SIM, ta có SM = \sqrt {S{I^2} + I{M^2}} = \frac{{R\sqrt {14} }}{2}

    Vậy {S_{\Delta SAB}} = \frac{1}{2}AB.SM = \frac{{{R^2}\sqrt 7 }}{2} (đvdt).

  • Câu 4: Vận dụng
    Tính đường cao nón

    Cho hình nón đỉnh S có đáy là hình tròn tâm O. Dựng hai đường sinh SA và SB, biết tam giác SAB vuông và có diện tích bằng 4a^2. Góc tạo bởi giữa trục SO và mặt phẳng (SAB) bằng 30^0. Đường cao h của hình nón bằng:

    Hướng dẫn:

     Tính đường cao nón

    Theo giả thiết ta có tam giác SAB vuông cân tại S.

    Gọi E là trung điểm AB, suy ra\left\{ \begin{array}{l}SE \bot AB\\OE \bot AB\end{array} ight.  và SE = \frac{1}{2}AB.

    Ta có {S_{\Delta SAB}} = \frac{1}{2}AB.SE = 4{a^2} \Leftrightarrow \frac{1}{2}AB.\frac{1}{2}AB = 4{a^2}

    \Rightarrow AB = 4a \Rightarrow SE = 2a.

    Gọi H là hình chiếu của O trên SE, suy ra OH \bot SE.

    Ta có \left\{ \begin{array}{l}AB \bot OE\\AB \bot SO\end{array} ight. \Rightarrow AB \bot \left( {SOE} ight) \Rightarrow AB \bot OH.

    Từ đó suy ra OH \bot \left( {SAB} ight) nên

    {30^0} = \widehat {SO,\left( {SAB} ight)} = \widehat {SO,SH} = \widehat {OSH} = \widehat {OSE}

    Trong tam giác vuông SOE, ta có SO = SE.\cos \widehat {OSE} = a\sqrt 3

  • Câu 5: Vận dụng
    Tính bán kính

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, . Cạnh bên , hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:

    Hướng dẫn:

    Tính bán kính

    Gọi M là trung điểm AC, suy ra SM \bot \left( {ABC} ight) \Rightarrow SM \bot AC.

    Tam giác SAC có SM là đường cao và cũng là trung tuyến nên tam giác SAC cân tại S.

    Ta có AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2, suy ra tam giác SAC đều.

    Gọi G là trọng tâm \triangle SAC , suy ra GS = GA = GC.    (1)

    Tam giác ABC vuông tại B, có M là trung điểm cạnh huyền AC nên M là tâm đường tròn ngoại tiếp tam giác ABC.

    Lại có SM \bot \left( {ABC} ight) nên SM là trục của tam giác ABC.

    Mà G thuộc SM nên suy ra GA = GB = GC.

    Từ (1) và (2), suy ra GS = GA = GB = GC hay G là tâm mặt cầu ngoại tiếp khối chóp S.ABC.

    Bán kính mặt cầu R = GS = \frac{2}{3}SM = \frac{{a\sqrt 6 }}{3}.

  • Câu 6: Nhận biết
    Diện tích toàn phần

    Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh có cạnh bằng 2R. Diện tích toàn phần của khối trụ bằng:

    Hướng dẫn:

    Do thiết diện đi qua trục hình trụ nên ta có h = 2R.

    Diện tích toàn phần là: {S_{tp}} = 2\pi R\left( {R + h} ight) = 6\pi {R^2} (đvdt).

  • Câu 7: Vận dụng
    Tỉ số giữa thể tích

    Một hình nón có đường cao bằng 9 cm nội tiếp trong một hình cầu bán kính bằng 5 cm. Tỉ số giữa thể tích khối nón và khối cầu là:

    Hướng dẫn:

    Tỉ số giữa thể tích

    Hình vẽ kết hợp với giả thiết, ta có SH = 9cm, OS=OA=5cm

    Suy ra OH = 4{m{cm}} và AH = \sqrt {O{A^2} - O{H^2}} = 3{m{cm}}{m{.}}

    Thể tích khối nón {V_n} = \frac{1}{3}\pi A{H^2}.SH = 27\pi(đvtt).

    Thể tích khối cầu {V_c} = \frac{4}{3}\pi .S{O^3} = \frac{{500\pi }}{3}  (đvtt).

    Suy ra \frac{{{V_n}}}{{{V_c}}} = \frac{{81}}{{500}}

  • Câu 8: Nhận biết
    Độ dài đường sinh

    Cho mặt cầu tâm O, bán kính R = a. Một hình nón có đỉnh S là ở trên mặt cầu và đáy là đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho SH = \frac{{3a}}{2}. Độ dài đường sinh \ell của hình nón bằng:

    Hướng dẫn:

    Độ dài đường sinh

    Gọi S' là điểm đối xứng của S qua tâm O và A là một điểm trên đường tròn đáy của hình nón.

    Tam giác SAS’ vuông tại A và có đường cao AH nên S{A^2} = SH.SS' \Rightarrow SA = a\sqrt 3 .

  • Câu 9: Thông hiểu
    Tính bán kính đáy

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài đường sinh bằng 2a thì bán kính đáy bằng:

    Hướng dẫn:

     Gọi bán kính đáy là R.

    Từ giả thiết suy ra h= 2a và chu vi đáy bằng a .

    Do đó 2\pi R = a \Leftrightarrow R = \frac{a}{{2\pi }}.

  • Câu 10: Vận dụng cao
    Thể tích khối trụ

    Cho khối trụ có hai đáy là (O) và \left(O^\primeight). AB,CD lần lượt là hai đường kính của (O) và \left(O^\primeight), góc giữa AB và CD bằng {30}^\circ,AB=6. Thể tích khối tứ diện ABCD bằng 30 . Thể tích khối trụ đã cho bằng?

    Hướng dẫn:

     Thể tích trụ

    Ta chứng minh: V_{ABCD}=\frac{1}{6}AB\cdot CD\cdot d(AB,CD)\cdot\sin(AB,CD)..

    Lấy điểm E sao cho tứ giác BCDE là hình bình hành.

    Khi đó  (AB,CD)=(AB,BE)\Rightarrow\sin(AB,CD)=\sin(AB,BE)..

    Mà góc giữa AB và CD bằng {30}^\circ,AB=6 nên ta có:

    \sin(AB,CD)=\sin(AB,BE)=\sin 30^0 =\frac 1 2

    Ta có d(D,(ABE))=d(AB, CD)

    V_{ABCD}=V_{ABDE}

    =\frac{1}{3}.d(D,(ABE)).S_{ABE}=\frac {1}{6} AB.CD.d(AB,CD).sin (AB,CD)

    Suy ra V_{ABCD}=\frac {1}{6} AB.CD.d(AB,CD).sin (AB,CD)

    Vậy d(AB,CD)=\dfrac{6V_{ABCD}}{AB.CD.\sin30^0}=\dfrac{180}{6.6.\dfrac{1}{2}}=10

    Chiều cao của lăng trụ bằng h = d(AB, CD)=10

    Áp dụng CT thể tích lăng trụ là: V=Sh=\pi .3^2.10=90 \pi

     

  • Câu 11: Thông hiểu
    Tính đường cao

    Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB, biết AB chắn trên đường tròn đáy một cung có số đo bằng 60^0, khoảng cách từ tâm O đến mặt phẳng (SAB) bằng \frac{R}{2}. Đường cao h của hình nón bằng:

    Hướng dẫn:

    Theo giả thiết ta có tam giác OAB đều cạnh R.

    Gọi E là trung điểm AB, suy ra OE \bot AB và OE = \frac{{R\sqrt 3 }}{2}.

    Gọi H là hình chiếu của O trên SE, suy ra OH \bot SE.

    Ta có \left\{ \begin{array}{l}AB \bot OE\\AB \bot SO\end{array} ight. \Rightarrow AB \bot \left( {SOE} ight) \Rightarrow AB \bot OH

    Từ đó suy ra OH \bot \left( {SAB} ight) nên d\left[ {O,\left( {SAB} ight)} ight] = OH = \frac{R}{2}.

    Trong tam giác vuông SOE, ta có  \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{E^2}}} = \frac{8}{{3{R^2}}} \Rightarrow SO = \frac{{R\sqrt 6 }}{4}

  • Câu 12: Nhận biết
    Diện tích toàn phần

    Cạnh bên của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 120^0. Diện tích toàn phần của hình nón là:

    Hướng dẫn:

    Diện tích toàn phần

    Gọi S là đỉnh, O là tâm của đáy, thiết diện qua trục là SAB.

    Theo giả thiết, ta có SA = 2a và \widehat {ASO} = 60^\circ.

    Trong tam giác SAO vuông tại O, ta có

    OA = SA.\sin 60^\circ = a\sqrt 3

    Vậy diện tích toàn phần:

    {S_{tp}} = \pi R\ell + \pi {R^2} = \pi .OA.SA + \pi {\left( {OA} ight)^2} = \pi {a^2}\left( {3 + 2\sqrt 3 } ight) (đvdt).

  • Câu 13: Vận dụng cao
    Thể tích khối trụ

    Cho hình trụ có O, O' là tâm hai đáy. Xét hình chữ nhật ABCD có A, B cùng thuộc (O) và C, D cùng thuộc (O') sao cho AB=a\sqrt3,BC=2a đồng thời (ABCD) tạo với mặt phẳng đáy hình trụ góc {60}^\circ . Thể tích khối trụ bằng

    Hướng dẫn:

     Thể tích khối trụ

    Gọi M,N lần lượt là trung điểm của CD,AB và I là trung điểm của OO^\prime. Suy ra góc giữa mặt phẳng (ABCD) và mặt phẳng đáy là  \widehat{IMO^\prime}={60}^\circ.

    Ta có IM=\frac{1}{2}MN=\frac{1}{2}BC=a..

    Xét \triangle IO^\prime M vuông tại O, ta có:

    IO^\prime=IM\cdot\sin\widehat{IMO^\prime}=\frac{a\sqrt3}{2}\Rightarrow h=OO^\prime=2IO^\prime=a\sqrt3;

    O^\prime M=IM\cdot\cos\widehat{IMO^\prime}=\frac{a}{2}

    Xét \triangle O^\prime MD vuông tại M, có O^\prime M=\frac{a}{2},MD=\frac{1}{2}CD=\frac{1}{2}AB=\frac{a\sqrt3}{2}

    \Rightarrow r=O^\prime D=\sqrt{O^\prime M^2+MD^2}=\sqrt{\left(\frac{a}{2}ight)^2+\left(\frac{a\sqrt3}{2}ight)^2}\Rightarrow r=a.

    Vậy V=\pi r^2h=\pi a^3\sqrt3.

  • Câu 14: Thông hiểu
    Vị trí tương đối

    Cho mặt phẳng \left( P ight):2x - 4y + 4z + 5 = 0 và mặt cầu \left( S ight):{x^2} + {y^2} + {z^2} - 2x + 4y + 2z - 3 = 0. Xét vị trí tương đối của mặt phẳng với mặt cầu?Cắt nhau || cắt nhau

    Đáp án là:

    Cho mặt phẳng \left( P ight):2x - 4y + 4z + 5 = 0 và mặt cầu \left( S ight):{x^2} + {y^2} + {z^2} - 2x + 4y + 2z - 3 = 0. Xét vị trí tương đối của mặt phẳng với mặt cầu?Cắt nhau || cắt nhau

    Theo đề bài, ta xác định các hệ số của (S): 

    a = 1;b = - 2;c = - 1;d = - 3 \Rightarrow R = 3.

    Suy ra tâm I có tọa độ là: I = \left( {1, - 2, - 1} ight)

    Áp dụng CT, ta có d\left( {I,P} ight) = \frac{{11}}{6} < R = 3 \Rightarrow (P) cắt (S)

  • Câu 15: Thông hiểu
    Tìm tập hợp các tâm

    Tìm tập hợp các tâm I của mặt cầu sau nằm trên?

    \left( S ight):{x^2} + {y^2} + {z^2} + 2\left( {1 - m} ight)x + 2\left( {3 - 2m} ight)y + 2\left( {m - 2} ight)z + 5{m^2} - 9m + 6 = 0

    Hướng dẫn:

    Theo đề bài, ta xác định các hệ số của (S): 

    a = m - 1;\,\,b = 2m - 3;\,\,c = 2 - m;\,\,d = 5{m^2} - 9m + 6

    Suy ra ta gọi được tâm I của mặt cầu có tọa độ là I\left( {x = m - 1;y = 2m - 3;z = 2 - m} ight)

    \Rightarrow x + 1 = \frac{{y + 3}}{2} = 2 - z

    Xét (S) là mặt cầu \Leftrightarrow {\left( {m - 1} ight)^2} + {\left( {2m - 3} ight)^2} + {\left( {2 - m} ight)^2} - 5{m^2} + 9m - 6 > 0

    \begin{array}{l} \Leftrightarrow {m^2} - 9m + 8 > 0 \Leftrightarrow m < 1 \vee m > 8\\ \Leftrightarrow m - 1 < 0 \vee m - 1 > 7 \Leftrightarrow x < 0 \vee x > 7\end{array}

    Vậy tập hợp các điểm I là phân đường thẳng  x + 1 = \frac{{y + 3}}{2} = 2 - z

    tương ứng với x < 0\,\,\, \vee \,\,\,x > 7.

  • Câu 16: Vận dụng
    Độ dài đường sinh

    Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và \widehat {SAO} = {30^0},\widehat {SAB} = {60^0}. Độ dài đường sinh \ell của hình nón bằng:

    Hướng dẫn:

     Độ dài đường sinh

    Gọi I là trung điểm AB, suy ra OI \bot AB,{m{ }}SI \bot AB và OI = a.

    Trong tam giác vuông SOA, ta có OA = SA.\cos \widehat {SAO} = \frac{{SA\sqrt 3 }}{2}

    Trong tam giác vuông SIA, ta có IA = SA.\cos \widehat {SAB} = \frac{{SA}}{2}

    Trong tam giác vuông OIA, ta có:

    O{A^2} = O{I^2} + I{A^2} \Leftrightarrow \frac{3}{4}S{A^2} = {a^2} + \frac{1}{4}S{A^2} \Rightarrow SA = a\sqrt 2 .

  • Câu 17: Vận dụng cao
    Diện tích xung quanh

    Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là một tam giác vuông  SAB có diện tích bằng 4a^2. Góc giữa trục SO và mặt phẳng (SAB) bằng {30}^\circ. Diện tích xung quanh của hình nón đã cho bằng?

    Hướng dẫn:

     

    Gọi M là trung điểm của AB , tam giác OAB cân đỉnh O nên OM\bot AB  và SO\bot AB suy ra AB\bot(SOM)

    Dựng OK\bot SM..

    Theo trên có OK\bot AB nên OK\bot(SAB).

    Vậy góc tạo bởi giữa trục SO và mặt phẳng (SAB) là \widehat{OSM}={30}^\circ. Tam giác vuông cân SAB có diện tích bằng 4a^2 suy ra \frac{1}{2}SA^2=4a^2\Rightarrow SA=2a\sqrt2

    \Rightarrow AB=4a\Rightarrow SM=2a..

    Xét tam giác vuông SOM có \cos\widehat{OSM}=\frac{SO}{SM}\Rightarrow SO=\frac{\sqrt3}{2}\cdot2a=\sqrt3a..

    Cuối cùng OB=\sqrt{SB^2-SO^2}=a\sqrt5.

    Vậy diện tích xung quanh của hình nón bằng S_{xq}=\pi rl=\pi\cdot a\sqrt5\cdot2a\sqrt2=2a^2\sqrt{10}\pi.

  • Câu 18: Nhận biết
    Tính diện tích

    Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R\sqrt 3. Diện tích xung quanh và diện tích toàn phần của hình lần lượt có giá trị là:

    Hướng dẫn:

    Diện tích xung quanh của hình trụ: {S_{xq}} = 2\pi R.R\sqrt 3 = 2\sqrt 3 \pi {R^2}(đvdt).

    Diện tích toàn phần của hình trụ:

    {S_{tp}} = {S_{xq}} + 2.{S_{{m{day}}}} = 2\sqrt 3 \pi {R^2} + 2\left( {\pi {R^2}} ight) = 2\left( {\sqrt 3 + 1} ight)\pi {R^2}(đvdt).

  • Câu 19: Nhận biết
    Diện tích của đường tròn giao tuyến

    Cho mặt cầu S(O;R) , A là một điểm ở trên mặt cầu (S) và (P) là mặt phẳng qua A sao cho góc giữa OA và (P) bằng 60^0. Diện tích của đường tròn giao tuyến bằng:

    Hướng dẫn:

    Diện tích của đường tròn giao tuyến

    Gọi H là hình chiếu vuông góc của (O) trên (P) thì

    ● H là tâm của đường tròn giao tuyến của (P) và (S).

    ●\widehat {OA,\left( P ight)} = \widehat {\left( {OA,AH} ight)} = {60^0}

    Bán kính của đường tròn giao tuyến: r = HA = OA.\cos {60^0} = \frac{R}{2}.

    Suy ra diện tích đường tròn giao tuyến: \pi {r^2} = \pi {\left( {\frac{R}{2}} ight)^2} = \frac{{\pi {R^2}}}{4}.

  • Câu 20: Vận dụng
    Tính bán kính

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Đường thẳng SA = a\sqrt 2 vuông góc với đáy (ABCD) . Gọi M là trung điểm SC, mặt phẳng (\alpha) đi qua hai điểm A và M đồng thời song song với BD cắt SB, SD lần lượt tại E và F. Bán kính mặt cầu đi qua năm điểm S, A, E, M, Fnhận giá trị nào sau đây?

    Hướng dẫn:

     Tính bán kính

    Mặt phẳng (\alpha) song song với BD cắt SB, SD lần lượt tại E, F nên EF||BD.

    \triangle SAC cân tại A , trung tuyến AM nên AM \bot SC  (1)

    Ta có \left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} ight. \Rightarrow BD \bot \left( {SAC} ight) \Rightarrow BD \bot SC

    Do đó EF \bot SC   (2)

    Từ (1) và (2), suy ra SC \bot \left( \alpha ight) \Rightarrow SC \bot AE   (*)

    Lại có \left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} ight. \Rightarrow BC \bot \left( {SAB} ight) \Rightarrow BC \bot AE  (**)

    Từ (*) và (**), suy ra AE \bot \left( {SBC} ight) \Rightarrow AE \bot SB. Tương tự ta cũng có AF \bot SD.

    Do đó \widehat {SEA} = \widehat {SMA} = \widehat {SFA} = {90^0} nên năm điểm S,{m{ }}A,{m{ }}E,{m{ }}M,{m{ }}F cùng thuộc mặt cầu tâm I là trung điểm của SA, bán kính R = \frac{{SA}}{2} = \frac{{a\sqrt 2 }}{2}.

  • Câu 21: Vận dụng
    Thể tích của khối nón

    Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn ngoại tiếp của đáy ABC đến một mặt bên là \frac{a}{2}. Thể tích của khối nón ngoại tiếp hình chóp SABC bằng:

    Hướng dẫn:

     Thể tích khối nón

    Gọi E là trung điểm của BC, dựng OH \bot SE tại H.

    Chứng minh được OH \bot \left( {SBC} ight) nên suy ra OH = d\left[ {O,\left( {SBC} ight)} ight] = \frac{a}{2}.

    Trong tam giác đều ABC, ta có OE = \frac{1}{3}AE = \frac{1}{3}.\frac{{2a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}

    và  OA = \frac{2}{3}AE = \frac{{2a\sqrt 3 }}{3}

    Trong tam giác vuông SOE, ta có

    \frac{1}{{O{H^2}}} = \frac{1}{{O{E^2}}} + \frac{1}{{S{O^2}}} \Rightarrow \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{E^2}}} = \frac{1}{{{a^2}}} \Rightarrow SO = a.

    Vậy thể tích khối nón V = \frac{1}{3}\pi O{A^2}.SO = \frac{1}{3}\pi {\left( {\frac{{2a\sqrt 3 }}{3}} ight)^2}.a = \frac{{4\pi {a^3}}}{9}  (đvtt).

  • Câu 22: Thông hiểu
    Vị trí tương đối của 2 mặt cầu

    Cho hai mặt cầu sau:

    \left( S ight):{x^2} + {y^2} + {z^2} - 4x + 6y - 10z - 11 = 0;

    \left( {S'} ight):{x^2} + {y^2} + {z^2} - 2x + 2y - 6z - 5 = 0

    Xét vị trí tương đối của 2 mặt cầu?

    Tiếp xúc trong || tiếp xúc trong

    Đáp án là:

    Cho hai mặt cầu sau:

    \left( S ight):{x^2} + {y^2} + {z^2} - 4x + 6y - 10z - 11 = 0;

    \left( {S'} ight):{x^2} + {y^2} + {z^2} - 2x + 2y - 6z - 5 = 0

    Xét vị trí tương đối của 2 mặt cầu?

    Tiếp xúc trong || tiếp xúc trong

     Theo đề bài, ta suy ra các hệ số, tâm và bán kính của (S):

    \left( S ight):a = 2;\,\,b = - 3;\,\,c = 5;\,\,d = - 11 \Rightarrow Tâm I\left( {2, - 3,5} ight); bán kính R=7

    \left( {S'} ight) = a' = 1;\,\,b' = - 1;\,c' = 3;\,\,d' = - 5 \Rightarrow Tâm J\left( {1, - 1,3} ight); bán kính R'=4

    I{J^2} = {\left( {1 - 2} ight)^2} + {\left( { - 1 + 3} ight)^2} + {\left( {3 - 5} ight)^2} = 9 \Rightarrow IJ = 3 = R - R'

    (S) và (S') tiếp xúc trong.

  • Câu 23: Thông hiểu
    Diện tích toàn phần

    Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Diện tích toàn phần của hình trụ bằng:

    Hướng dẫn:

    Diện tích toàn phần

    Theo giả thiết ta được hình trụ có chiều cao h=AB=1 , bán kính đáy R = \frac{{AD}}{2} = 1

    Do đó diện tích toàn phần: {S_{tp}} = 2\pi Rh + 2\pi {R^2} = 4\pi

  • Câu 24: Nhận biết
    Chọn câu đúng

    Cho đường tròn (C) đường kính AB và đường thẳng \triangle. Để hình tròn xoay sinh bởi (C) khi quay quanh \triangle là một mặt cầu thì cần có thêm điều kiện nào sau đây:

    Hướng dẫn:

    Điều kiện để hình tròn xoay sinh bởi (C) khi quay quanh \triangle là một mặt cầu là trục quay \triangle phải cố định và hai điểm A, B cũng cố định trên \triangle.

  • Câu 25: Nhận biết
    Tính khoảng cách

    Cho mặt cầu S(O; R) và một điểm A, biết OA = 2R. Qua A kẻ một cát tuyến cắt (S) tại B và C sao cho BC = R\sqrt 3. Khi đó khoảng cách từ O đến BC bằng:

    Hướng dẫn:

     Gọi H là hình chiếu của O lên BC.

    Ta có OB=OC=R , suy ra H là trung điểm của BC nên HC = \frac{{CD}}{2} = \frac{{R\sqrt 3 }}{2}

    Suy ra OH = \sqrt {O{C^2} - H{C^2}} = \frac{R}{2}.

  • Câu 26: Thông hiểu
    Thể tích của khối trụ

    Cho hình trụ có chiều cao bằng 8a . Biết hai điểm A và C lần lượt nằm trên hai đáy thỏa mãn AC=10a, khoảng cách giữa AC và trục của hình trụ bằng 4a. Thể tích của khối trụ đã cho là:

    Hướng dẫn:

      Thể tích của khối trụ

    Gọi (O) và (O') lần lượt là hai đường tròn đáy; A\in (O), C \in (O') .

    Dựng AD, CB lần lượt song song với OO' (D \in (O'), B \in (O). Dễ dàng có ABCD là hình chữ nhật.

    Do AC=10a,AD=8a\Rightarrow DC=6a..

    Gọi H là trung điểm của DC.

    \left\{\begin{matrix}O^\prime H\bot D C\\O^\prime H\bot A D\\\end{matrix}\Rightarrow O^\prime H\bot(ABCD)ight..

    Ta có O^\prime//(ABCD)\Rightarrow d\left(OO^\prime,ACight)=d\left(OO^\prime,(ABCD)ight)=O^\prime H=4a..

    Suy ra O^\prime H=4a,CH=3a\Rightarrow R=O^\prime C=5a..

    Vậy thể tích của khối trụ là V=\pi R^2h=\pi(5a)^28a=200\pi a^3.

  • Câu 27: Nhận biết
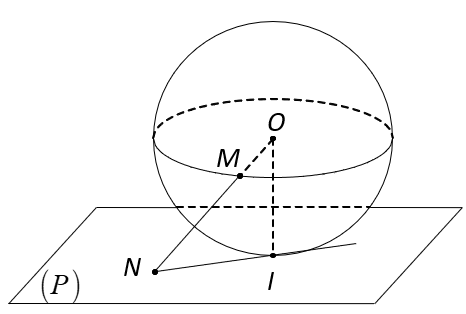
    Mệnh đề đúng

    Cho mặt cầu (S) tâm O, bán kính R và mặt phẳng (P) có khoảng cách đến O bằng R. Một điểm M tùy ý thuộc (S). Đường thẳng OM cắt (P) tại N. Hình chiếu của O trên (P) là I. Mệnh đề nào sau đây đúng?

    Hướng dẫn:

     Mệnh đề đúng

    Vì I là hình chiếu của O trên (P) nên  d\left[ {O,\left( P ight)} ight] = OI mà d\left[ {O,\left( P ight)} ight] = R nên I là tiếp điểm của (P) và (S).

    Đường thẳng OM cắt (P) tại N nên IN vuông góc với OI tại I.

    Suy ra IN tiếp xúc với (S).

    Tam giác OIN vuông tại I nên ON = R\sqrt 2 \Leftrightarrow IN = R.

  • Câu 28: Nhận biết
    Thể tích khối trụ

    Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng a. Thể tích khối trụ bằng:

    Hướng dẫn:

     Do thiết diện đi qua trục hình trụ nên ta có h=a.

    Bán kính đáy R = \frac{a}{2}. Do đó thể tích khối trụ V = {R^2}\pi .h = \frac{{\pi {a^3}}}{4}(đvtt).

  • Câu 29: Vận dụng
    Tìm tập hợp các điểm M

    Cho mặt cầu (S): {x^2} + {y^2} + {z^2} - 4x + 6y + 2z - 2 = 0 và điểm A\left( { - 6, - 1,3} ight). Gọi M là tiếp điểm của (S) và tiếp tuyến di động qua (d). Tìm tập hợp các điểm M.

    (Có thể chọn nhiều đáp án)

    Hướng dẫn:

     Theo đề bài, (S) có tâm I\left( {2, - 3,1} ight).\,\overrightarrow {IM} = \left( {x - 2,y + 3,z + 1} ight);\,\,\overrightarrow {AM} = \left( {x + 6,y + 1,z - 3} ight)

    Ta có:

    \begin{array}{l}\overrightarrow {IM} .\overrightarrow {AM} = \left( {x - 2} ight)\left( {x + 6} ight) + \left( {y + 3} ight)\left( {y + 1} ight) + \left( {z + 1} ight)\left( {z - 3} ight) = 0\\ \Rightarrow M \in \left( {S'} ight):{x^2} + {y^2} + {z^2} + 4x + 4y - 3z - 12 = 0;\,\,M \in \left( S ight)\end{array}

    \Rightarrow M \in  đường tròn  \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} - 4x + 6y + 2z - 2 = 0\\4x - y - 2z - 5 = 0\end{array} ight.

    Hay \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} + 4x + 4y - 2z - 12 = 0\\4x - y - 2z - 5 = 0\end{array} ight.

  • Câu 30: Thông hiểu
    Viết phương trình mặt cầu

    Cho hình lập phương OABC.DEFG có cạnh bằng 1 có \overrightarrow {OA} ,\,\,\overrightarrow {OC} ,\,\,\overrightarrow {OG} trùng với ba trục \overrightarrow {Ox} ,{m{ }}\overrightarrow {Oy} ,{m{ }}\overrightarrow {Oz}. Viết phương trình mặt cầu \left( {{S_3}} ight) tiếp xúc với tất cả các cạnh của hình lập phương.

    Hướng dẫn:

     \left( {{S_2}} ight) tiếp xúc với 12 cạnh của hình lập phương tại trung điểm của mỗi cạnh.

    Tâm I\left( {\frac{1}{2},\frac{1}{2},\frac{1}{2}} ight) là trung điểm chng của 6 đoạn nối trung điểm của các cặp cạnh đối diện đôi một có độ dài bằng \sqrt 2

    Bán kính {R_3} = \frac{{\sqrt 2 }}{2}

    \begin{array}{l} \Rightarrow \left( {{S_2}} ight):{\left( {x - \dfrac{1}{2}} ight)^2} + {\left( {y - \dfrac{1}{2}} ight)^2} + {\left( {z - \dfrac{1}{2}} ight)^2} = \dfrac{1}{2}\\ \Rightarrow \left( {{S_3}} ight):{x^2} + {y^2} + {z^2} - x - y - z + \dfrac{1}{4} = 0\end{array}

0/30
30 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (30%):
    2/3
  • Thông hiểu (30%):
    2/3
  • Vận dụng (30%):
    2/3
  • Vận dụng cao (10%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 1 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập