Tính thể tích hình lăng trụ ABCD.EFGH, biết ![]() và
và ![]() .
.
Áp dụng công thức tính thể tích lăng trụ:
Theo đề bài, ta có:
Áp dụng CT tính thể tích khối lăng trụ:
Suy ra: .
Tính thể tích hình lăng trụ ABCD.EFGH, biết ![]() và
và ![]() .
.
Áp dụng công thức tính thể tích lăng trụ:
Theo đề bài, ta có:
Áp dụng CT tính thể tích khối lăng trụ:
Suy ra: .
Hai đường thẳng ![]() và
và ![]()
Ta có đường thẳng (d’) qua E (-1, -1, 0) có vecto chỉ phương
Hai pháp vecto của hai đường thẳng lần lượt là
Vecto chỉ phương của
Ta có: và tọa độ
thỏa mãn phương trình của
Trong không gian Oxyz cho vectơ ![]() và
và ![]() . Gọi
. Gọi ![]() lần lượt là ba góc tạo bởi
lần lượt là ba góc tạo bởi ![]() với ba trục
với ba trục ![]() . Ta có:
. Ta có:
Áp dụng công thức hình chiếu vecto trên trục, ta có ngay được:
Viết phương trình tổng quát của mặt phẳng ![]() qua hai điểm
qua hai điểm ![]() và song song với trục
và song song với trục ![]()
Vì Vecto chỉ phương của (P) là:
Theo đề bài, ta có vecto chỉ phương thứ hai của (P) là:
Từ 2 VTCP, ta suy ra được VTPT của (P) là tích có hướng của 2 VTCT
Mp (P) đi qua và nhận vecto
làm 1 VTPT có phương trình là:
Cho tứ diện ![]() có
có ![]() . Phương trình tổng quát của mặt phẳng chứa AC và song song với BD là:
. Phương trình tổng quát của mặt phẳng chứa AC và song song với BD là:
Theo đề bài, ta có các vecto là
Có thể chọn làm một vectơ pháp tuyến cho mặt phẳng.
Phương trình mặt phẳng này có dạng .
Mặt khác, điểm A thuộc mặt phẳng nên ta thay tọa độ điểm A vào phương trình đường thẳng trên:
Vậy phương trình cần tìm .
Viết phương trình tổng quát của mặt phẳng ![]() cắt hai trục
cắt hai trục ![]() và
và ![]() tại và tạo với mặt phẳng
tại và tạo với mặt phẳng ![]() một góc
một góc ![]() .
.
Gọi là giao điểm của
và trục
Vecto pháp tuyến của là:
Vecto pháp tuyến của là:
Gọi là góc tạo bởi và
Vậy có hai mặt phẳng:
Cho hình hộp chữ nhật OABC.DEFG có ![]() . Gọi L là tâm hình hộp. Biểu thị vectơ
. Gọi L là tâm hình hộp. Biểu thị vectơ ![]() theo ba vectơ
theo ba vectơ ![]() và
và ![]() ?
?
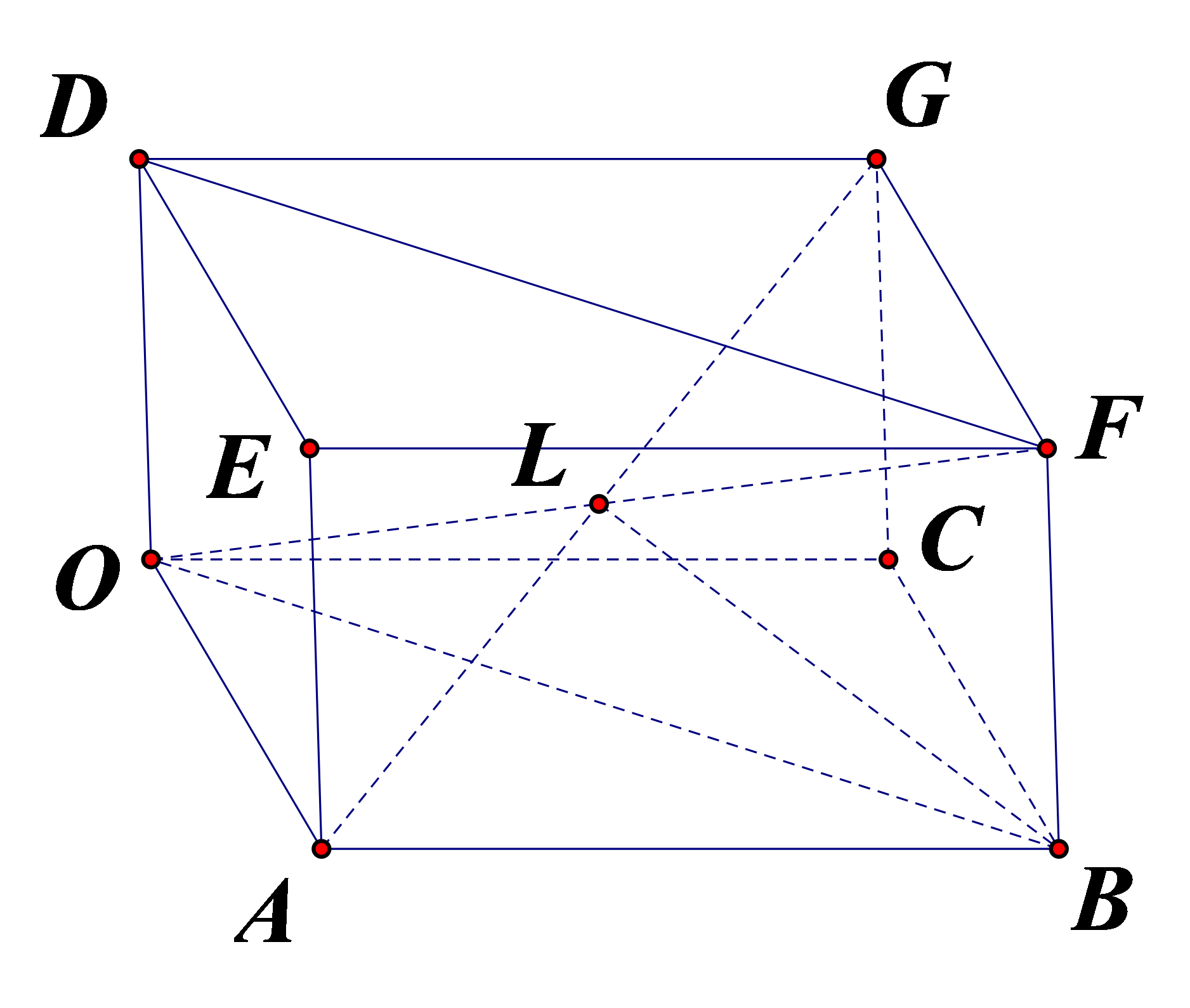
Vì I là tâm hình hộp theo giả thiết nên I là trung điểm đường chéo OF. Từ đây, suy ra
Cho ba điểm ![]() . Tìm tọa độ của C để tam giác ABC là tam giác vuông cân tại A.
. Tìm tọa độ của C để tam giác ABC là tam giác vuông cân tại A.
Tam giác ABC vuông cân tại A
Viết phương trình tham số của đường thẳng ![]()
Theo đề bài, đường thẳng d là giao của 2 mặt phẳng, ta gọi 2 mặt phẳng (P) và (Q) tương ứng lần lượt là:
Mp (P) và (Q) có 2 vecto pháp tuyến tương ứng là:
Từ đây ta suy ra vecto chỉ phương của đường thẳng (d) là tích có hướng của 2 VTPT:
Cho y = 0, ta có:
Đường thẳng (d) đi qua A( 1, 0, 2) và nhận vecto (1,2,4) làm 1 VTCP có PTTS là:
Viết phương trình tổng quát của mặt phẳng (P) qua ![]() và song song với mặt phẳng (Q):
và song song với mặt phẳng (Q): ![]()
Vì mp nên ta có PTTQ mp
sẽ có dạng là:
Mặt khác, (P) qua
Hai đường thẳng  và
và  với cắt nhau tại M có tọa độ là :
với cắt nhau tại M có tọa độ là :
Để (d’) cắt (d) tại
Cho ba điểm ![]() .
.
Tam giác ABC là tam giác?
Để biết tam giác ABC là tam giác gì, ta cần xét tích vô hướng (tính chất có 1 góc vuông) và kiểm tra độ dài 3 cạnh AB, BC, CA (tính cân, đều) của tam giác. Ta có:
Suy ra tam giác ABC có góc nên vuông tại A.
Ta tiếp tục xét tính cân:
Vậy tam giác ABC vuông cân tại A.
Phân tích vectơ ![]() theo ba vectơ không đồng phẳng
theo ba vectơ không đồng phẳng
![]()
Ta có 3 vecto không đồng phẳng. Khi đó luôn có :
Cho hai đường thẳng 
Viết phương trình tổng quát của mặt phẳng (P) qua (d’)và song song với (d’’).
Vì (P) đi qua (d’) nên (P) nhận VTCP của (d’) làm 1 VTCP
Vì (P) song song với (d’’) nên (P) có VTCP thứ hai là :
Từ đây, ta suy ra VTPT của (P) chính là tích có hướng của 2 VTCP và :
Lấy điểm A(3,1,-2) trên đường thẳng (d’) mà (d’) nằm trong (P) nên ta có được A cũng phải thuộc (P):
Cho hai đường thẳng trong không gian Oxyz: ![]() ,
, ![]() . Với
. Với ![]() . Gọi
. Gọi ![]() và
và ![]() . (D) và (d) song song khi và chỉ khi:
. (D) và (d) song song khi và chỉ khi:
Để xét điều kiện (D) và (d) cắt nhau ta cẩn kiểm tra rằnng (D) và d cùng nằm trong 1 mặt phẳng hay ta có:
và (d) cùng nằm trong một mặt phẳng
Để (D) và d song song, ta sẽ xét tỉ số chứng minh chúng cùng phương rồi kiểm tra rằng d không nằm trong (D):
và (d) cùng phương
và
và (d) song song.
Cho hai đường thẳng trong không gian Oxyz: ![]() ,
, ![]() . Với
. Với ![]() . Gọi
. Gọi ![]() và
và ![]() . (D) và (d) chéo nhau khi và chỉ khi:
. (D) và (d) chéo nhau khi và chỉ khi:
Để xét điều kiện (D) và (d) có chéo nhau hay không, ta cẩn kiểm tra rằng (D) và d không cùng nằm trong 1 mặt phẳng hay ta có:
Suy ra (D) và (d) chéo nhau.
Cho ba điểm ![]() . Tính
. Tính ![]() để
để ![]() là trọng tâm tam giác ABC?
là trọng tâm tam giác ABC?
Vì G là trọng tâm tam giác ABC nên áp dụng công thức, ta có:
Thay tọa độ các điểm vào ta được hệ sau:
Trong không gian Oxyz cho hai vectơ![]() khác
khác ![]() cùng phương. Câu nào sau đây sai? (có thể chọn 2 đáp án)
cùng phương. Câu nào sau đây sai? (có thể chọn 2 đáp án)
Ta xét đáp án : sai vì thiếu điều kiện
.
Xét đáp án : luôn đúng vì 2 vecto cùng phương với nhau.
Ta xét tiếp: : cũng sai, vì thiếu điều kiện
Như vậy ta sẽ chọn 2 đáp án có 2 ý sai.
Cho hình hộp chữ nhật ABCD.EFGH có ![]() trong hệ trục Oxyz sao cho A trùng với
trong hệ trục Oxyz sao cho A trùng với ![]() lần lượt trùng với Ox, Oy, Oz. Gọi M, N, P lần lượt là trung điểm BC, EF, DH. Tính khoảng cách giữa NP và CG.
lần lượt trùng với Ox, Oy, Oz. Gọi M, N, P lần lượt là trung điểm BC, EF, DH. Tính khoảng cách giữa NP và CG.
Ta biểu diễn các điểm N, P, C, G theo a, b, c được:
Từ đó, ta tính được các vecto tương ứng:
Để tính khoảng cách giữa NP và CG, ta cần tính tích có hướng và tích độ dài giữa chúng rồi áp dụng CT tính khoảng cách:
Cho M trên đường thẳng AB với ![]() và
và ![]() . Nếu
. Nếu ![]() với
với ![]() thì tọa độ của M là:
thì tọa độ của M là:
Vì M nằm trên AB và nên khi xét theo tọa độ vecto 2 điểm A và B, ta có:
Cho tam giác ABC với ![]() .
.
Viết phương trình tổng quát của mặt phẳng ![]() vuông góc với mặt phẳng
vuông góc với mặt phẳng ![]() song song đường cao AH của tam giác ABC.
song song đường cao AH của tam giác ABC.
Theo đề bài, ta có: song song đường cao
Phương trình tổng quát của mặt phẳng đi qua A(4, -1, 1), B(3, 1, -1) và song song với trục Ox là:
: vectơ chỉ phương của trục Ox:
.
: Chọn làm vectơ pháp tuyến thì phương trình mặt phẳng cần tìm có dạng
, qua A nên:
Vậy ta có phương trình mp cần tìm là:
Phương trình tổng quát của mặt phẳng qua A(3,-1, 2), B(4, -2, -1), C(2, 0, 2) là:
Theo đề bài, ta có được các vecto sau:
Vì mặt phẳng đi qua 3 điểm nên VTPT của mp là tích có hướng của và
.
Chọn làm một vectơ pháp tuyến.
Phương trình mp có dạng
là mp qua A
Vậy phương trình .
Cho hai đường thẳng (d1 ): ![]() và
và ![]()
Xét VTTĐ của (d1 ) và (d2 )? Tìm câu đúng ?
Chuyển đường thẳng (d1 ) và (d2 ) về dạng tham số :
có vectơ chỉ phương
và qua
.
có vectơ chỉ phương
và hệ phương trình
vô nghiệm.
.
Cho mặt phẳng ![]() qua điểm
qua điểm ![]() và chắn trên ba trục tọa độ
và chắn trên ba trục tọa độ ![]() theo ba đoạn có số đo đại số a, b, c. Viết phương trình tổng quát của
theo ba đoạn có số đo đại số a, b, c. Viết phương trình tổng quát của ![]() khi a, b, c tạo thành một cấp số nhân có công bội bằng 2.
khi a, b, c tạo thành một cấp số nhân có công bội bằng 2.
Theo đề bài, ta có a, b, c là cấp số nhân với công bội q=2
Phương trình của
(P) qua
Cho hai điểm ![]() . Viết phương trình tổng quát của mặt phẳng
. Viết phương trình tổng quát của mặt phẳng ![]() vuông góc với AB, cắt ba trục tọa độ Ox, Oy, Oz tại M, N, E sao cho thể tích hình chóp
vuông góc với AB, cắt ba trục tọa độ Ox, Oy, Oz tại M, N, E sao cho thể tích hình chóp ![]() bằng
bằng ![]() đvtt.
đvtt.
Vecto pháp tuyến của
Phương trình
cắt 3 trục tọa độ tại
Thể tích hình chóp là:
Viết phương trình tổng quát của đường thẳng (d) qua A (2, 3, 1) cắt đường thẳng ![]() và vuông góc đường thẳng
và vuông góc đường thẳng ![]()
Lấy điểm nằm trên đường thẳng (d1).
Theo đề bài, ta có (d1) qua có vecto chỉ phương là
Ta có:
Vecto pháp tuyến của mặt phẳng (P) chứa A và
(1)
Xét tiếp đường thẳng có vecto chỉ phương của là vecto pháp tuyến của mặt phẳng qua A và vuông góc với . Ta có phương trình mp (Q) là
(2)
Từ (1) và (2) ta suy ra:
Cho ba điểm ![]() . Tính x và y để ba điểm A, B, C đã cho thẳng hàng với nhau?
. Tính x và y để ba điểm A, B, C đã cho thẳng hàng với nhau?
Áp dụng điều kiện để 3 điểm thẳng hàng :
thẳng hàng
cùng phương với
rồi xét hệ
A, B, C thẳng hàng cùng phương với
Cho tứ giác ABCD có ![]() . Viết phương trình của mặt phẳng (P) qua A, B và chia tứ diện thành hai khối ABCE và ABDE có tỉ số thể tích bằng 3.
. Viết phương trình của mặt phẳng (P) qua A, B và chia tứ diện thành hai khối ABCE và ABDE có tỉ số thể tích bằng 3.

Theo đề bài, ta có mp (P) cắt cạnh CD tại E, E chia đoạn CD theo tỷ số -3
Từ đó, ta suy ra:
Như vậy, VTPT mp (P) là:
Cho hai mặt phẳng ![]() Đường thẳng (D) qua M (1, -2, 3) song song với (P) và (Q):
Đường thẳng (D) qua M (1, -2, 3) song song với (P) và (Q):
Vì (D) song song với (P) và (Q)
=> Một vectơ chỉ phương của (D) là:
Xét vecto pháp tuyến của (R), có:
Xét đáp án có điểm N
cùng phương với
=> (D) vuông góc với (S).
