Tổng quan về số phức
Bài học Lí thuyết toán 12: Tổng quan về số phức bao gồm các vấn đề cơ bản liên quan đến số phức như: cách biểu diễn hình học số phức, mô đun của số phức và số phức liên hợp. Bên cạnh đó, trong bài học này đã kèm theo những ví dụ bài tập đều có hướng dẫn giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12.
1. Biểu diễn hình học số phức
Mỗi số phức ![]() hoàn toàn được xác định bởi cặp số thực
hoàn toàn được xác định bởi cặp số thực ![]() .
.
Điểm ![]() trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức
trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức ![]()
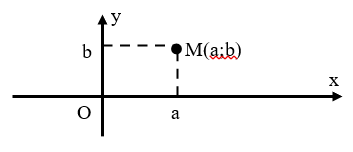
Hay ta nói, số phức ![]() được biểu diễn bởi điểm
được biểu diễn bởi điểm ![]() hay bởi
hay bởi ![]() trong mp(Oxy) (mp phức)
trong mp(Oxy) (mp phức)
Ví dụ:
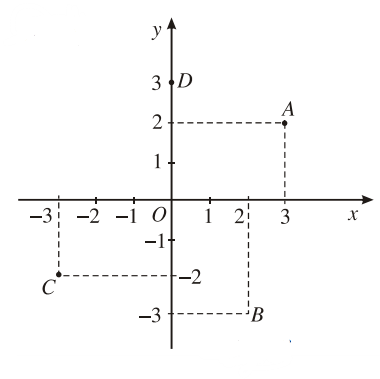
Điểm A biểu diễn số phức ![]()
Điểm B biểu diễn số phức ![]()
Điểm C biểu diễn số phức ![]()
Điểm D biểu diễn số phức ![]()
2. Mô đun của số phức
Giả sử số phức ![]() được biểu diễn bởi điểm
được biểu diễn bởi điểm ![]() trong một hệ tọa độ . Độ dài của vecto
trong một hệ tọa độ . Độ dài của vecto ![]() được gọi là môđun của số phức
được gọi là môđun của số phức ![]() và kí hiệu
và kí hiệu ![]() .
.
Vậy
![]()
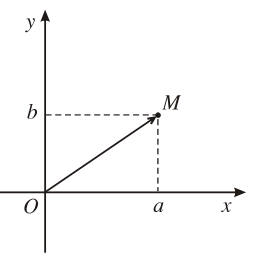
Như vậy, ta có thể có công thức liên quan giữa modun số phức và độ dài vecto như sau:
![]()
![]()
Nhận xét: Cho số phức ![]() ;
; ![]() ta có:
ta có:
Ví dụ: Số phức ![]() có mô đun được tính như sau:
có mô đun được tính như sau:

3. Số phức liên hợp
Cho số phức ![]() . Ta gọi số phức liên hợp của
. Ta gọi số phức liên hợp của ![]() là
là ![]() .
.
Trên mặt phẳng tọa độ, các điểm biểu diễn ![]() và
và ![]() đối xứng với nhau qua trục Ox.
đối xứng với nhau qua trục Ox.
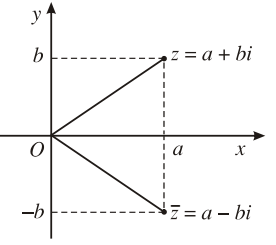
Nhận xét: Cho số phức ![]() ;
; ![]() ta có:
ta có:
 ;
; 



 là số thực
là số thực  ;
;  là số thuần ảo
là số thuần ảo 
Ví dụ: Cho số phức ![]() .
.
Tính các số phức sau: ![]()
Vì ![]()
![]()
Ta có



Ta có: ![]()
![]()
Nội dung cùng chủ đề
-
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
Chương 2: Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
Chương 3: Nguyên hàm - Tích phân và ứng dụng
-
Chương 4: Số phức
-
Chương 1 Hình: Khối đa diện
-
Chương 2 Hình: Mặt nón, mặt trụ, mặt cầu
-
Chương 3: Phương pháp tọa độ trong không gian
-
Ôn thi Học kì







