Lớp 12 Toán 12

Hàm số lũy thừa

Bài học Lí thuyết toán 12: Hàm số lũy thừa giới thiệu cho các em khái niệm về hàm số lũy thừa, công thức tính đạo hàm của hàm số lũy thừa và khảo sát hàm số lũy thừa y=x^{\alpha}. Bên cạnh đó là các ví dụ bài tập có lời giải chi tiết giúp các em dễ dàng ôn tập củng cố.

1. Khái niệm

Xét hàm số y=x^{\alpha}, với \alpha là số thực cho trước.

Hàm số y=x^{\alpha}, với \alpha \in \mathbb{R}, được gọi là hàm số lũy thừa.

Chú ý:

Tập xác định của hàm số lũy thừa y=x^{\alpha} tùy thuộc vào giá trị của . Cụ thể:

  • Với \alpha nguyên dương, tập xác định là \mathbb{R}
  • Với \alpha nguyên âm hoặc bằng 0, tập xác định là \mathbb{R}\backslash \left\{ 0 \right\}
  • Với \alpha không nguyên, tập xác định \left( {0; + \infty } \right)

2. Đạo hàm của hàm số lũy thừa

 Cho hàm số lũy thừa  y=x^{\alpha}, với \alpha \in \mathbb{R}. Khi đó, ta có công thức tổng quát:

\boxed{ (x^{\alpha})' = \alpha x^{\alpha -1}}

Ví dụ: Tính đạo hàm?

a) (x^{\frac {-2}{3}})'=\frac{-2}{3}x^{\frac {5}{3}}=\frac{-2}{3\sqrt[3]{x^5} }

b) (x^{2023})'=2023.x^{-2022}

3. Khảo sát hàm số lũy thừa y=x^{\alpha}

Tập xác định của hàm số lũy thừa y=x^{\alpha} luôn chứa khoảng \left( {0; + \infty } \right) 

với mọi \alpha \in \mathbb{R}. Trong trường hợp tổng quát, ta khảo sát hàm số y=x^{\alpha} trên khoảng này.

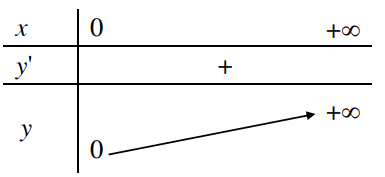
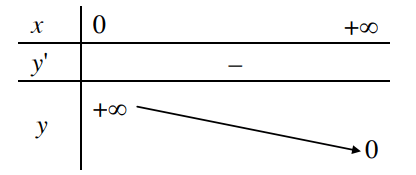
Ta có bảng tổng kết sau:

y = {x^\alpha },\alpha > 0

y = {x^\alpha },\alpha < 0

1. Tập xác định:

\left( {0; + \infty } \right)

2. Sự biến thiên

y' = \alpha .{x^{\alpha - 1}} > 0

{\forall x > 0}

Giới hạn đặc biệt:

\mathop {\lim }\limits_{x \to {0^ + }} {x^\alpha } = 0\begin{array}{*{20}{c}} ,&{\mathop {\lim }\limits_{x \to + \infty } } \end{array}{x^\alpha } = + \infty .

Tiệm cận: không có.

3. Bảng biến thiên

1. Tập xác định:

\left( {0; + \infty } \right)

2. Sự biến thiên

y' = \alpha .{x^{\alpha - 1}} < 0

{\forall x > 0}

Giới hạn đặc biệt:

\mathop {\lim }\limits_{x \to {0^ + }} {x^\alpha } = + \infty \begin{array}{*{20}{c}} ,&{\mathop {\lim }\limits_{x \to + \infty } } \end{array}{x^\alpha } = 0.

Tiệm cận:

  • Ox là tiệm cận ngang.
  • Oy là tiệm cận đứng.

3. Bảng biến thiên

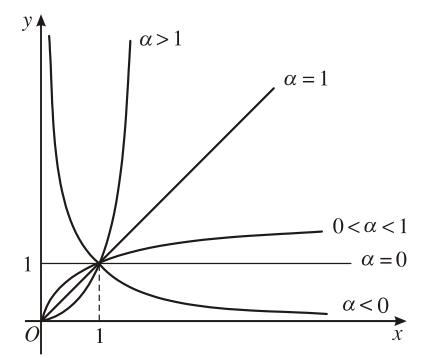
Đồ thị của hàm số

Đồ thị của hàm số lũy thừa y=x^{\alpha} luôn đi qua điểm I\left( {1;1} \right).

 

Câu trắc nghiệm mã số: 1759, 1758,1755,1754,1752,1747,1745,1746
  • 12 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12