Định nghĩa và tính chất của nguyên hàm

Bộ tài liệu Lí thuyết toán 12: Nguyên hàm bao gồm định nghĩa, tính chất nguyên hàm và các bài tập ứng dụng có hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia.

A. Nguyên hàm là gì?

Cho hàm số xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số được gọi là nguyên hàm của hàm số trên K nếu với mọi x thuộc K.

Minh họa trực quan:

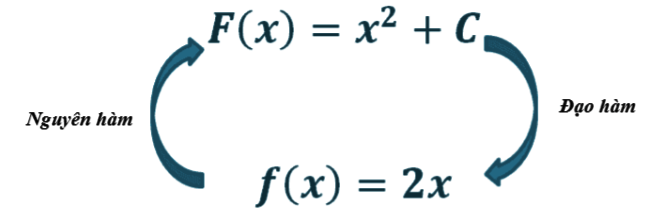Ví dụ: là một nguyên hàm của hàm số vì

Định lí 1: Nếu F(x) là một nguyên hàm của hàm số trên K thì với mỗi hằng số C thì hàm số cũng là một nguyên hàm của trên K.

Chứng minh ĐL1: 

Do là một nguyên hàm của hàm số f(x) nân ta có

Khi 

Vậy   cũng là một nguyên hàm của hàm số

Định lí 2: Nếu F(x) là một nguyên hàm của hàm số trên K thì mọi nguyên hàm của hàm số trên K đều có dạng với C là một hằng số.

Chứng minh ĐL2:

Giả sử G(x) cũng là một nguyên hàm của f(x) trên K, ta có . 

Khi đó

Suy ra   (C là hàm số không đổi)

Định lí 3: Mọi hàm số liên tục trên K đều có nguyên hàm trên K

B. Tính chất nguyên hàm

Nếu và là hai hàm số liên tục trên K thì:

Tính chất 1: 

Tính chất 2: với k là số thực khác 0

Tính chất 3: với a, b là hai số thực khác 0

Tính chất 4: Với và ta có:

Một số ví dụ:

Ví dụ 1: Tính nguyên hàm của hàm số

Hướng dẫn giải

Ví dụ 2: Nguyên hàm của hàm số

Hướng dẫn giải