Đồ thị hàm số ![]() có điểm cực tiểu và điểm cực đại nằm về hai phía trục tung khi:
có điểm cực tiểu và điểm cực đại nằm về hai phía trục tung khi:
Ta có:
Đồ thị có điểm cực đại và cực tiểu khi và chỉ khi y’ = 0 có hai nghiệm
Theo định lí Vi – et ta có:
Hai điểm cực trị nằm về hai phía trục tung khi và chỉ khi
Đồ thị hàm số ![]() có điểm cực tiểu và điểm cực đại nằm về hai phía trục tung khi:
có điểm cực tiểu và điểm cực đại nằm về hai phía trục tung khi:
Ta có:
Đồ thị có điểm cực đại và cực tiểu khi và chỉ khi y’ = 0 có hai nghiệm
Theo định lí Vi – et ta có:
Hai điểm cực trị nằm về hai phía trục tung khi và chỉ khi
Tập xác định của hàm số ![]() là:
là:
Hàm số xác định khi
Vậy tập xác định của hàm số là
Có bao nhiêu giá trị nguyên của m để hàm số ![]() xác định với mọi
xác định với mọi ![]() ?
?
Hàm số xác định với mọi
=>
Vì m nguyên nên
Vậy có tất cả 7 giá trị của m thỏa mãn điều kiện đề bài.
Cho đồ thị ba hàm số trên khoảng như hình vẽ. Mệnh đề nào sau đây đúng?
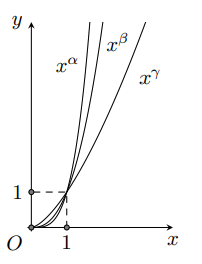
Từ đồ thị ta thấy
Với thì
Với thì
Cho biểu thức ![P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.{{\left( {{a^2}{b^2}} ight)}^{\frac{2}{3}}}} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6}](https://i.khoahoc.vn/data/image/holder.png) với a và b là các số thực dương. Khẳng định nào sau đây là đúng?
với a và b là các số thực dương. Khẳng định nào sau đây là đúng?
Thực hiện thu gọn biểu thức như sau:
Trong các biểu thức sau, biểu thức nào có nghĩa?
Tập xác định của hàm số tùy thuộc vào
Với nguyên dương, tập xác định
Với nguyên âm hoặc bằng 0, tập xác định
Với không nguyên, tập xác định là
Ta có: có
là số nguyên âm nên cơ số
=> có nghĩa
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
Ta có: nên hàm số nghịch biến trên tập xác định của nó.
Đạo hàm của hàm số ![]()
Ta có:
Cho biết ![]() . Tính
. Tính
![]()
Ta có:
Bố bạn Nam gửi 15000 USD vào trong ngân hàng theo hình thức lãi kép với lãi suất 0,73% một tháng để dành cho Nam học đại học. Nếu cuối cùng mỗi tháng kể từ ngày gửi Nam rút tiền đều đặn 300USSD (trừ tháng cuối) thì sai bao nhiêu tháng số tiền để dành cho Nam sẽ được rút hết? (tháng cuối là tháng mà số tiền còn trong ngân hàng không vượt 300USSD và khi đó Nam rút hết toàn bộ số tiền còn lại).
Gọi An là số tiền còn lại sau khi nam rút đến tháng thứ n, A là số tiền gủi vào, r là lãi suất hàng tháng và X là số tiền rút ra hàng tháng
Ta có:
Vậy
Áp dụng vào bài toán ta có:
Tập xác định của hàm số ![]() là:
là:
Điều kiện xác định:
=> Tập xác định của hàm số là
Cho hàm số ![]() . Tính
. Tính ![]()
Ta có:
Cho một số thực ![]() tùy ý. Trong các khẳng định sau khẳng định nào đúng?
tùy ý. Trong các khẳng định sau khẳng định nào đúng?
Theo tính chất đạo hàm của hàm số lũy thừa, hàm số có đạo hàm với mọi x > 0 và
Biết rằng tập tất cả các giá trị thực của tham số m để hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() và
và ![]() là đoạn
là đoạn ![]() . Tính
. Tính ![]()
Tập xác định
Hàm số đã cho đồng biến trên tức là
Xét
Ta có:
Ta có bảng biến thiên
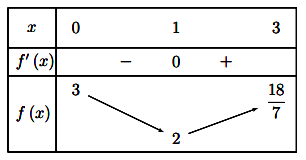
Từ bảng biến thiên suy ra
Hàm số đã cho đồng biến trên tức là
Xét ta có:
Ta có bảng biến thiên như sau:
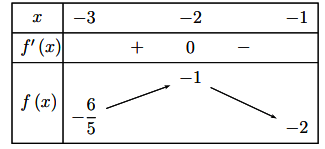
Từ bảng biến thiên suy ra
Kết hợp kết quả ta được
Đạo hàm của hàm số ![]()
Ta có:
Phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm thuộc đồ thị hàm số có hoành độ bằng 1 là:
tại điểm thuộc đồ thị hàm số có hoành độ bằng 1 là:
Ta có:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm thuộc đồ thị hàm số có hoành độ bằng 1 là:
Cho hàm số ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Hàm số có các tính chất như sau:
Đồ thị hàm số nhận trục tung làm tiệm cận đứng
Đồ thị hàm số nhận trục hoành làm tiệm cận ngang
Là hàm số nghịch biến trên
Tập xác định của hàm số ![]() là:
là:
Điều kiện xác định của hàm số là:
=> Tập xác định của hàm số là:
Cho biết năm 2018, tỉnh A có 2 triệu người và tỉ lệ dân số là 1,4%/năm. Hỏi đến năm 2025 tỉnh A có bao nhiêu người, nếu tỉ lệ tăng dân số hằng năm không đổi?
Công thức ước tính dân số
Trong đó A là dân số của nam lấy làm mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hằng năm.
Ta có: A = 2, n = 7; I = 0,014
Số dân tỉnh A đến năm 2025 là triệu người.
Cho hàm số ![]() . Tính
. Tính ![]()
Tập xác định
Ta có:
