Hệ tọa độ trong không gian
Bài học Lí thuyết toán 12: Hệ tọa độ trong không gian đã đưa ra cho các em những vấn đề cơ bản nhất về Hình không gian như: tọa độ điểm, vecto; biểu thức tọa độ; tích vô hướng, có hướng giữa hai vecto. Mỗi mục kiến thức đều kèm theo những ví dụ bài tập có hướng dẫn giải chi tiết.
1. Hệ tọa độ trong không gian
1.1. Hệ tọa độ
Trong không gian, xét ba trục ![]() vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi
vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi ![]() lần lượt là các vectơ đơn vị các trục
lần lượt là các vectơ đơn vị các trục ![]() . Hệ ba trục như vậy gọi là hệ trục tọa độ Đề-các vuông góc
. Hệ ba trục như vậy gọi là hệ trục tọa độ Đề-các vuông góc ![]() trong không gian hay hệ tọa độ
trong không gian hay hệ tọa độ ![]() .
.
Điểm O được gọi là gốc tọa độ.
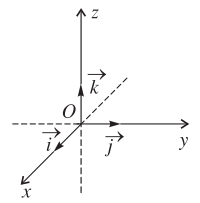
Chú ý: ![]() và
và ![]() .
.
1.2. Tọa độ của một điểm
Định nghĩa:
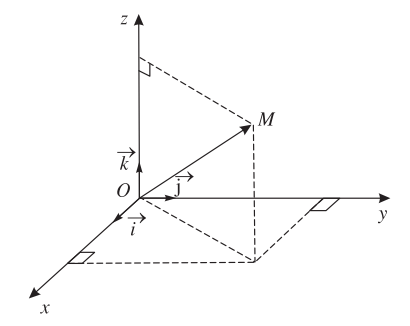
Trong không gian ![]() , cho một điểm M tùy ý sao cho
, cho một điểm M tùy ý sao cho
![]()
(x : hoành độ, y : tung độ, z : cao độ)
Khi đó, bộ ba số ![]() duy nhất là tọa độ của điểm M.
duy nhất là tọa độ của điểm M.
Chú ý:
![]() ·
·
Ví dụ:
![]()
1.3. Tọa độ vectơ
Định nghĩa:
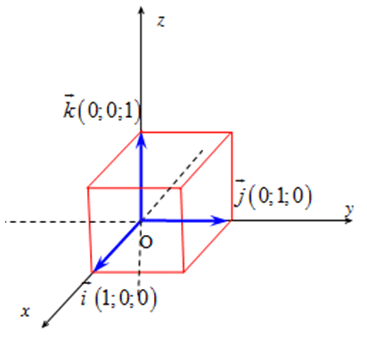
Trong không gian ![]() cho vecto
cho vecto ![]() , tọa độ của
, tọa độ của ![]() là bộ ba số
là bộ ba số ![]() khi:
khi:![]()
Ví dụ:
![]()
2. Biểu thức tọa độ
2.1. Định lý
Trong không gian ![]() cho hai vecto
cho hai vecto ![]() .
.
Ta có:
2.2. Hệ quả
Cho ![]()
- Công thức 2 vecto bằng nhau:

- Tọa độ vecto
 và các vecto đơn vị:
và các vecto đơn vị:
![]()
- Điều kiện để có 2 vecto cùng phương
![]() cùng phương
cùng phương ![]()
![]()

![]()
- Điều kiện để có 2 vecto vuông góc
![]()
2.3. Hệ quả mở rộng
Cho ![]()
- Toạ độ trung điểm M của đoạn thẳng AB:
![]()
- Toạ độ trọng tâm G của tam giác ABC:

- Toạ độ trọng tâm G của tứ diện ABCD:

3. TÍCH VÔ HƯỚNG
3.1. Biểu thức tọa độ của tích vô hướng
Trong không gian ![]() , tích vô hướng của 2 vecto
, tích vô hướng của 2 vecto ![]() được các định bởi công thức:
được các định bởi công thức:
![]()
3.2. Ứng dụng
- Độ dài của 1 vecto
Cho vecto ![]() , khi đó:
, khi đó: ![]()
- Khoảng cách giữa hai điểm
Cho ![]() , khi đó ta có:
, khi đó ta có:
![]()
![]()
- Góc giữa hai vecto
Cho ![]() , khi đó:
, khi đó:

(với ![]() )
)
Ví dụ:
Cho ![]() và
và ![]() . Để góc giữa hai vectơ
. Để góc giữa hai vectơ ![]() có số đo bằng
có số đo bằng ![]() thì m bằng bao nhiêu?
thì m bằng bao nhiêu?
Giải:
Theo đề bài, ta có:
![]()

![]()
4. Tích có hướng của hai vectơ
4.1.Định nghĩa
Trong không gian cho hai vectơ ![]() . Tích có hướng của hai vectơ
. Tích có hướng của hai vectơ ![]() và
và ![]() kí hiệu là
kí hiệu là ![]() , được xác định bởi
, được xác định bởi
![]()
![]()
Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.
4.2.Tính chất
![[\overrightarrow a ,\,\,\overrightarrow b ]\,\, \bot \,\,\overrightarrow a ;\,\,\,\,\,[\overrightarrow a ,\,\,\overrightarrow b ]\,\, \bot \,\,\overrightarrow b](https://i.khoahoc.vn/data/image/holder.png)
![\left[ {\overrightarrow a ,\,\,\overrightarrow b \,} \right] = - \left[ {\overrightarrow b ,\overrightarrow a } \right]](https://i.khoahoc.vn/data/image/holder.png)
![\left[ {\vec i,\vec j} \right] = \vec k;\,\,\,\,\,\,\left[ {\vec j,\vec k} \right] = \vec i;\,\,\,\,\,\left[ {\vec k,\vec i} \right] = \vec j](https://i.khoahoc.vn/data/image/holder.png)
![\left| {[\overrightarrow a ,\,\overrightarrow b ]} \right|\,\, = \,\left| {\vec a} \right|.\left| {\vec b} \right|.\sin \left( {\vec a,\vec b} \right)](https://i.khoahoc.vn/data/image/holder.png) (Chương trình nâng cao)
(Chương trình nâng cao) cùng phương
cùng phương ![\Leftrightarrow \,\,\,[\overrightarrow a ,\,\,\overrightarrow b ]\,\, = \,\,\overrightarrow 0](https://i.khoahoc.vn/data/image/holder.png) (chứng minh 3 điểm thẳng hàng)
(chứng minh 3 điểm thẳng hàng)
4.3. Ứng dụng: (mở rộng)
- Điều kiện đồng phẳng của ba vectơ:
 và
và  đồng phẳng
đồng phẳng ![\Leftrightarrow [\overrightarrow a ,\,\,\overrightarrow b ]\,.\overrightarrow c = 0](https://i.khoahoc.vn/data/image/holder.png)
- Diện tích hình bình hành ABCD :
![{S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right|](https://i.khoahoc.vn/data/image/holder.png)
- Diện tích tam giác ABC :
![{S_{\Delta ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\,\,\overrightarrow {AC} } \right]} \right|](https://i.khoahoc.vn/data/image/holder.png)
- Thể tích khối hộp ABCDA'B'C'D':
![{V_{ABCD.A'B'C'D'}}\,\, = \,\,\left| {[\overrightarrow {AB} ,\,\,\overrightarrow {AD} ].\overrightarrow {AA'} } \right|](https://i.khoahoc.vn/data/image/holder.png)
- Thể tích tứ diện ABCD:
![{V_{ABCD}} = \frac{1}{6}\left| {[\overrightarrow {AB} ,\,\,\overrightarrow {AC} ]\,.\overrightarrow {AD} } \right|](https://i.khoahoc.vn/data/image/holder.png)
Ví dụ:
Cho ![]() . Thể tích của tứ diện ABCD là?
. Thể tích của tứ diện ABCD là?
Giải:
Ta tính tọa độ các vecto sau:
![]()
Như vậy, áp dụng công thức tính thể tích tứ diện, ta được:
![]()
Chú ý:
– Tích vô hướng của hai vectơ thường sử dụng để chứng minh hai đường thẳng vuông góc, tính góc giữa hai đường thẳng.
– Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương.
Nội dung cùng chủ đề
-
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
Chương 2: Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
Chương 3: Nguyên hàm - Tích phân và ứng dụng
-
Chương 4: Số phức
-
Chương 1 Hình: Khối đa diện
-
Chương 2 Hình: Mặt nón, mặt trụ, mặt cầu
-
Chương 3: Phương pháp tọa độ trong không gian
-
Ôn thi Học kì







