Đường thẳng (d): ![]() có phương trình tham số là:
có phương trình tham số là:
Ta có đường thẳng (d) qua A ( 2, -1, 4) và có vectơ chỉ phương là có phương trình tham số là:
=> (d)
Đường thẳng (d): ![]() có phương trình tham số là:
có phương trình tham số là:
Ta có đường thẳng (d) qua A ( 2, -1, 4) và có vectơ chỉ phương là có phương trình tham số là:
=> (d)
Cho tam giác ABC có ![]() .
.
Viết phương trình chính tắc của cạnh AB.
(AB) là đường thẳng đi qua A và B nên có 1 vecto chỉ phương:
(AB) đi qua A (1, 2, -3) và nhận vecto làm 1 VTCP có phương trình chính tắc là:
Hai đường thẳng ![]() và
và ![]()
Ta có đường thẳng (d’) qua E (-1, -1, 0) có vecto chỉ phương
Hai pháp vecto của hai đường thẳng lần lượt là
Vecto chỉ phương của
Ta có: và tọa độ
thỏa mãn phương trình của
Trong không gian Oxyz, cho mặt phẳng ![]() và hai điểm
và hai điểm ![]() . Trong các đường thẳng đi qua A và song song (P), đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất có phương trình là:
. Trong các đường thẳng đi qua A và song song (P), đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất có phương trình là:
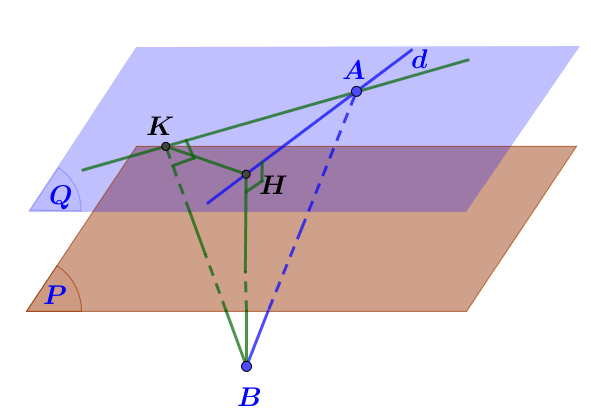
Gọi (Q) là mặt phẳng qua A và song song (P).
Ta có: nằm về hai phía với (P).
Gọi H là hình chiếu vuông góc của B lên (Q) BH cố định và
.
Gọi K là hình chiếu vuông góc của B lên bất kì qua A và nằm trong (Q) hay .
Ta có: bé nhất bằng BH khi K trùng với điểm H.
Gọi là VTPT của (ABH)
Ta có đường thẳng d cần lập qua A, H và có VTCP là
Vậy phương trình đường thẳng d cần lập là:
Hai đường thẳng ![]() và
và ![]() cắt nhau tại điểm A. Tọa độ của A là:
cắt nhau tại điểm A. Tọa độ của A là:
Để tìm được A là giao điểm của 2 đường thẳng, ta sẽ xét và giải hệ PT giữa chúng.
Từ phương trình của ,tính x,y theo z được
Thế vào phương trình của , được z = - 4 .
Từ đó suy ra x = 1, y = - 2
Cho hai đường thẳng: ![]()
và mặt phẳng ![]() .
.
Hình chiếu của ![]() theo phương của
theo phương của ![]() lên mặt phẳng
lên mặt phẳng ![]() có phương trình tổng quát:
có phương trình tổng quát:
Vectơ chỉ phương của Vectơ chỉ phương của
Phương trình của mặt phẳng chứa và có phương của
có dạng:
Điểm A (7, 3, 9) thuộc mặt phẳng này
=> D = -53
Giao tuyến của mặt phẳng này với mặt phẳng là hình chiếu của
theo phương của
lên
:
Cho tam giác ABC có ![]()
Viết phương trình tham số của trung tuyến AM ?
Vì AM là trung tuyến nên M là trung điểm của BC. Gọi
Từ tọa độ của B và C, ta tính được tọa độ của M là nghiệm của hệ:
Ta có 1 vecto chỉ phương của (AM) là
(AM) là đường thẳng đi qua A (1,2,-3) và nhận vecto (3,-7,15) làm 1 VTCP có phương trình là:
Cho hình hộp chữ nhật ![]() có
có ![]() trong hệ trục Oxyz sao cho A trùng với
trong hệ trục Oxyz sao cho A trùng với ![]() lần lượt trùng với
lần lượt trùng với ![]() . Gọi M, N, P lần lượt là trung điểm của BC, EF, DH. Viết phương trình tổng quát của giao tuyến (d) của mặt phẳng (MNP) và (xOy)
. Gọi M, N, P lần lượt là trung điểm của BC, EF, DH. Viết phương trình tổng quát của giao tuyến (d) của mặt phẳng (MNP) và (xOy)
Theo đề bài, ta biểu diễn được tọa độ các trung điểm M và N theo a, b, c lần lượt là:
Như vậy ta tính được vecto và
theo a, b, c.
(MNP) có vecto pháp tuyến là tích có hướng của 2 vecto và
(MNP) có đi qua M và nhận làm 1 VTCP có phương trình là:
Trong không gian với hệ trục tọa độ Oxyz , cho điểm A(3; -1; 0) và đường thẳng d: ![]() . Mặt phẳng
. Mặt phẳng ![]() chứa d sao cho khoảng cách từ A đến lớn nhất có phương trình là:
chứa d sao cho khoảng cách từ A đến lớn nhất có phương trình là:
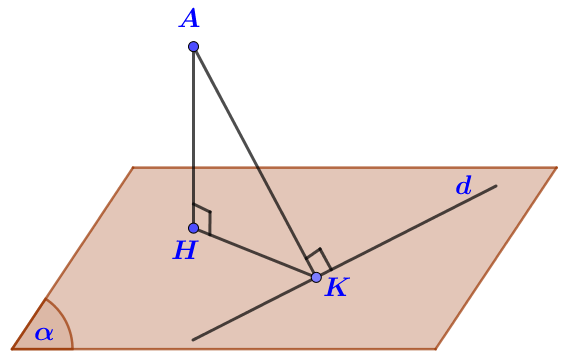
Gọi H là hình chiếu vuông góc của A lên , K là hình chiếu vuông góc của A lên d.
Ta có: cố định và
Suy ra lớn nhất bằng AK khi
.
Ta có (d): qua M(2; -1; 1) , có VTCP
.
Gọi (P) là mặt phẳng qua A và chứa có VTPT .
Mặt phẳng có một VTPT là
và
qua M (2; -1; 1) có phương trình:
Cho hai đường thẳng trong không gian Oxyz: ![]() ,
, ![]() . Với
. Với ![]() . Gọi
. Gọi ![]() và
và ![]() . (D) và (d) song song khi và chỉ khi:
. (D) và (d) song song khi và chỉ khi:
Để xét điều kiện (D) và (d) cắt nhau ta cẩn kiểm tra rằnng (D) và d cùng nằm trong 1 mặt phẳng hay ta có:
và (d) cùng nằm trong một mặt phẳng
Để (D) và d song song, ta sẽ xét tỉ số chứng minh chúng cùng phương rồi kiểm tra rằng d không nằm trong (D):
và (d) cùng phương
và
và (d) song song.
Cho đường thẳng  và mặt phẳng
và mặt phẳng ![]() . Mặt phẳng (P) qua d và tạo với
. Mặt phẳng (P) qua d và tạo với ![]() một góc nhỏ nhất. Một véc tơ pháp tuyến của (P) là:
một góc nhỏ nhất. Một véc tơ pháp tuyến của (P) là:
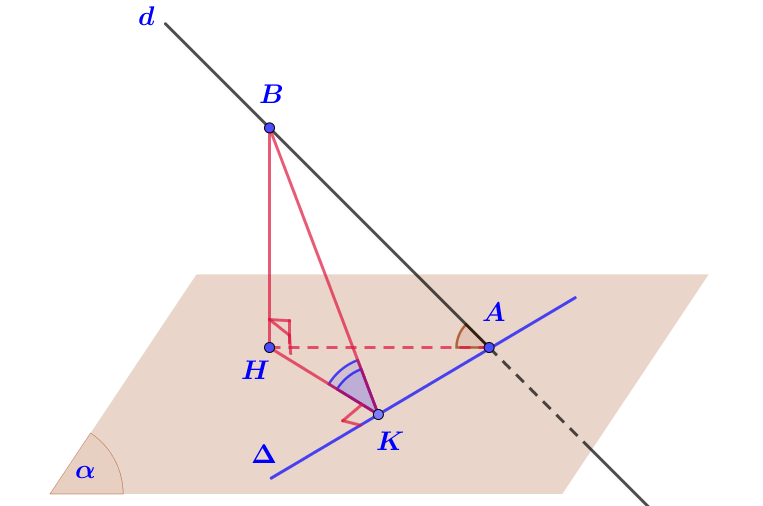
Gọi ;
H là hình chiếu vuông góc của B lên ; K là hình chiếu của H lên
.
Suy ra: cố định;
.
Mà (vì
)
Suy ra nhỏ nhất bằng
khi
.
Khi đó và có một VTCP
.
Vậy (P) có một VTPT là .
Tìm tọa độ giao điểm của hai đường thẳng:
Theo đề bài, ta biến đổi được (b) có dạng:
Thay x, y, z vào phương trình x+2y+z =9 , ta có:
=> Tọa độ giao điểm của (a) và (b): A (0, - 4, - 1)
Viết phương trình tham số của đường thẳng d qua hai điểm: ![]()
Để viết PT Tham số của một đường thẳng, ta cần 1 vecto chỉ phương và 1 điểm bất kỳ nằm trên đường thẳng đó.
Đường thẳng d đi qua hai điểm A và B nên VTCP của đường thẳng d chính là hay ta có:
Tính góc của hai đường thẳng ![]() và
và ![]() .
.
Theo đề bài, ta có (d’) và (d) có vec-tơ chỉ phương lần lượt là:
Áp dụng công thức cosin của góc giữa 2 đường thẳng, ta có:
Khoảng cánh giữa hai đường thẳng : ![]() và
và ![]() là:
là:
Chuyển d1 về dạng tham số :
Qua đó, ta có và 1 vectơ chỉ phương của (d1):
.
Chuyển (d2) về dạng tham số :
Qua đó, ta có và 1 vectơ chỉ phương của
Áp dụng công thức tính Khoảng cách d1 và d2 , ta được:
.
Cho hai đường thẳng 
Viết phương trình tổng quát của mặt phẳng (P) qua (d’)và song song với (d’’).
Vì (P) đi qua (d’) nên (P) nhận VTCP của (d’) làm 1 VTCP
Vì (P) song song với (d’’) nên (P) có VTCP thứ hai là :
Từ đây, ta suy ra VTPT của (P) chính là tích có hướng của 2 VTCP và :
Lấy điểm A(3,1,-2) trên đường thẳng (d’) mà (d’) nằm trong (P) nên ta có được A cũng phải thuộc (P):
Cho hai đường thẳng trong không gian Oxyz: ![]() ,
, ![]() . Với
. Với ![]() . Gọi
. Gọi ![]() và
và ![]() . (D) và (d) chéo nhau khi và chỉ khi:
. (D) và (d) chéo nhau khi và chỉ khi:
Để xét điều kiện (D) và (d) có chéo nhau hay không, ta cẩn kiểm tra rằng (D) và d không cùng nằm trong 1 mặt phẳng hay ta có:
Suy ra (D) và (d) chéo nhau.
Cho hai đường thẳng trong không gian Oxyz: ![]() ,
, ![]() . Với
. Với ![]() . Gọi
. Gọi ![]() và
và ![]() . (D) và (d) cắt nhau khi và chỉ khi:
. (D) và (d) cắt nhau khi và chỉ khi:
Để xét điều kiện (D) và (d) cắt nhau ta cẩn kiểm tra rằnng (D) và d cùng nằm trong 1 mặt phẳng hay ta có:
và (d) cùng nằm trong một mặt phẳng
Để (D) và d cắt nhau, ta sẽ xét tỉ số sau:
và (d) cắt nhau.
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình đường phân
giác trong góc A là ![]() . Biết rằng điểm
. Biết rằng điểm ![]() thuộc đường thẳng AB và điểm
thuộc đường thẳng AB và điểm ![]() thuộc đường thẳng AC. Véc tơ nào sau đây là véc tơ chỉ phương của đường thẳng AC?
thuộc đường thẳng AC. Véc tơ nào sau đây là véc tơ chỉ phương của đường thẳng AC?
Giả sử , , ta có:
Theo bài ra: Vì d là đường phân giác của góc A nên:
Từ đây ta bình phương 2 vế được:
Vậy một véc tơ chỉ phương của AC là .
Cho điểm P(-3 , 1, -1) và đường thẳng (d): ![]()
Điểm P' đối xứng với P qua đường thẳng (d) có tọa độ:
Chuyển (d) về dạng tham số :
Gọi (Q) là Mặt phẳng có vectơ chỉ phương của (d) có dạng: , cho qua P tính được D=7 .
Ta có (Q): .
Thế x, y, z theo t từ phương trình của (d) vào phương trình (Q) được
Giao điểm I của (d) và (Q) là I (1, -3, 1) .
Vì I là trung điểm của PP’ nên .
