Lớp 12

Đề Ôn tập chương 2 (Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 30 câu
  • Điểm số bài kiểm tra: 30 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Tập xác định của hàm số lũy thừa

    Tập xác định của hàm số f\left( x ight) = {\left( {x - 2} ight)^{ - 1}} là:

    Hướng dẫn:

    Điều kiện xác định của hàm số là:

    x - 2 e 0 \Rightarrow x e 2

    => Tập xác định của hàm số là: D = \mathbb{R}\backslash \left\{ 2 ight\}

  • Câu 2: Nhận biết
    Giá trị của biểu thức

    Giá trị của biểu thức {\log _2}5.{\log _5}64 là:

    Hướng dẫn:

    Ta có: {\log _2}5.{\log _5}64 = {\log _2}64 = {\log _2}{2^6} = 6

  • Câu 3: Vận dụng
    Chọn mệnh đề đúng

    Cho hình vẽ sau là đồ thị của ba hàm số y = {x^\alpha };y = {x^\beta };y = {x^\gamma } với x > 0 và \alpha ;\beta ;\gamma là các số thực cho trước, mệnh đề nào sau đây đúng?

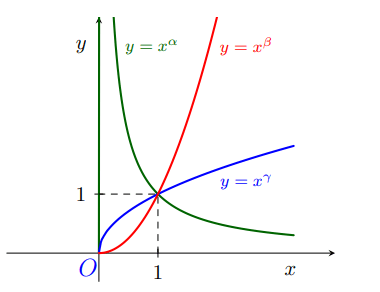
    Chọn mệnh đề đúng

    Hướng dẫn:

    Hàm số {x^\alpha } nghịch biến trên \alpha < 0

    Các hàm số y = {x^\beta };y = {x^\gamma } đồng biến nên \beta ;\gamma > 0

    Tại x = 3 thì {3^\beta } > {3^\gamma } \Rightarrow \beta > \gamma

  • Câu 4: Nhận biết
    Trong các khẳng định trên có bao nhiêu khẳng định đúng?

    Cho hàm số y = {x^{ - \frac{1}{2}}}. Cho các khẳng định sau:

    i) Hàm số xác định với mọi x

    ii) Đồ thị hàm số luôn đi qua điểm (1; 1)

    iii) Hàm số nghịch biến trên \mathbb{R}

    iv) Đồ thị hàm số có hai đường tiệm cận

    Trong các khẳng định trên có bao nhiêu khẳng định đúng?

    Hướng dẫn:

    Ta có khẳng định ii) và iv) là đúng

    i) Sai vì hàm số đã cho xác định khi x > 0

    iii) Sai vì hàm số nghịch biến trên \left( {0; + \infty } ight)

  • Câu 5: Nhận biết
    Chọn khẳng định sai?

    Cho hai số thực a và b với a > 0;a e 1;b e 0. Chọn khẳng định sai?

    Hướng dẫn:

    \frac{1}{2}{\log _a}{b^2} = {\log _a}b sai vì chưa biết b > 0 hay b < 0

  • Câu 6: Vận dụng
    Tính tích 2 nghiệm

    Gọi x_1, x_2 là 2 nghiệm của phương trình \frac{1}{{4 + {{\log }_2}x}} + \frac{2}{{2 - {{\log }_2}x}} = 1. Khi đó x_1.x_2 bằng:

    Hướng dẫn:

     Điều kiện: \left\{ \begin{gathered} x > 0 \hfill \\ x e 4 \hfill \\ x e \frac{1}{{16}} \hfill \\ \end{gathered} ight..

    Đặt t = {\log _2}x ,điều kiện \left\{ \begin{gathered} t e - 4 \hfill \\ t e 2 \hfill \\ \end{gathered} ight.. Khi đó phương trình trở thành:

    \frac{1}{{4 + t}} + \frac{2}{{2 - t}} = 1 \Leftrightarrow {t^2} + 3t + 2 = 0 \Leftrightarrow \left[ \begin{gathered} t = - 1 \hfill \\ t = - 2 \hfill \\ \end{gathered} ight. \Rightarrow \left[ \begin{gathered} x = \frac{1}{2} \hfill \\ x = \frac{1}{4} \hfill \\ \end{gathered} ight.

    Vậy {x_1}.{x_2} = \frac{1}{8}.

  • Câu 7: Thông hiểu
    Tính giá trị của biểu thức P

    Cho {\log _a}b = 2;{\log _a}c = 3. Tính giá trị của biểu thức P = {\log _a}\left( {a{b^3}{c^3}} ight)

    Hướng dẫn:

    Ta có:

    \begin{matrix} P = {\log _a}\left( {a{b^3}{c^3}} ight) \hfill \\ = {\log _a}a + {\log _a}{b^3} + {\log _a}{c^3} \hfill \\ = 1 + 3{\log _a}b + 5{\log _a}c \hfill \\ = 1 + 3.2 + 5.3 = 22 \hfill \\ \end{matrix}

  • Câu 8: Vận dụng
    Tính giá trị biểu thức P = ab

    Cho {9^x} + {9^{ - x}} = 14;\frac{{6 + 3.\left( {{3^x} + {3^{ - x}}} ight)}}{{2 - {3^{x + 1}} - {3^{1 - x}}}} = \frac{a}{b}; (\frac{a}{b} là phân số tối giản). Tính giá trị biểu thức P = ab.

    Hướng dẫn:

    Ta có:

    \begin{matrix} {\left( {{3^x} + {3^{ - x}}} ight)^2} = 14 + 2 = 16 \hfill \\ \Rightarrow {3^x} + {3^{ - x}} = 4 \hfill \\ \Rightarrow \dfrac{a}{b} = \dfrac{{6 + 3.4}}{{2 - 3.4}} = - \dfrac{9}{5} \hfill \\ \Rightarrow P = - 45 \hfill \\ \end{matrix}

  • Câu 9: Thông hiểu
    Khẳng định nào dưới đây đúng?

    Cho đồ thị hàm số y = {x^{ - \sqrt 2 }}. Khẳng định nào dưới đây đúng?

    Hướng dẫn:

     Theo định nghĩa của hàm số lũy thừa, đồ thị hàm số có tiệm cận đứng là x = 0

    Ta có: \mathop {\lim }\limits_{x \to + \infty } y = 0 suy ra đồ thị hàm số có tiệm cận ngang là y = 0

    Vậy đồ thị hàm số có tiệm cận ngang là y = 0 và tiệm cận đứng là x = 0

  • Câu 10: Thông hiểu
    Giá trị của biểu thức

    Biết {\log _2}3 = a;{\log _2}5 = b,  khi đó {\log _{15}}8 có giá trị là:

    Hướng dẫn:

    Ta có:

    {\log _{15}}8 = {\log _{15}}{2^3} = 3{\log _{15}}2 = \frac{3}{{{{\log }_2}15}} = \frac{3}{{{{\log }_2}3 + {{\log }_2}5}} = \frac{3}{{a + b}}

  • Câu 11: Vận dụng
    Tìm nghiệm nguyên lớn nhất

    Nghiệm nguyên lớn nhất của bất phương trình là:

    x=7 || X=7 || x bằng 7 || 7

    Đáp án là:

    Nghiệm nguyên lớn nhất của bất phương trình là:

    x=7 || X=7 || x bằng 7 || 7

     Điều kiện: x>0

    Ta có: \log _2^4x - \log _{\frac{1}{2}}^2\left( {\frac{{{x^3}}}{8}} ight) + 9{\log _2}\left( {\frac{{32}}{{{x^2}}}} ight) < 4\log _{{2^{ - 1}}}^2\left( x ight)

    \Leftrightarrow \log _2^4x - {\left( {3{{\log }_2}x - 3} ight)^2} + 9\left( {5 - 2{{\log }_2}x} ight) - 4\log _2^2x < 0

    \Leftrightarrow \log _2^4x - 13\log _2^2x + 36 < 0

    \Leftrightarrow 4 < \log _2^2x < 9 \Leftrightarrow \left[ \begin{gathered} 2 < {\log _2}x < 3 \hfill \\ - 3 < {\log _2}x < - 2 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} 4 < x < 8 \hfill \\ \frac{1}{8} < x < \frac{1}{4} \hfill \\ \end{gathered} ight..

    Vậy nghiệm nguyên lớn nhất của bất phương trình là: x=7.

  • Câu 12: Thông hiểu
    Trong các khẳng định sau khẳng định nào đúng?

    Cho một số thực \alpha tùy ý. Trong các khẳng định sau khẳng định nào đúng?

    Hướng dẫn:

     Theo tính chất đạo hàm của hàm số lũy thừa, hàm số y = {x^\alpha } có đạo hàm với mọi x > 0 và \left( {{x^\alpha }} ight)' = \alpha {x^{\alpha - 1}}

  • Câu 13: Vận dụng
    Tính giá trị của y

    Với các số thực dương x, y ta có: {8^x};{a^4};2 theo thứ tự lập thành một cấp số nhân và các số {\log _2}45;{\log _2}y;{\log _2}x theo thứ tự lập thành một cấp số cộng. Khi đó y bằng:

    Hướng dẫn:

    Ta có: 

    Từ {8^x};{a^4};2 theo thứ tự lập thành một cấp số nhân nên công bội q = \frac{2}{{{4^4}}} = \frac{1}{{{2^7}}}

    \Rightarrow {4^4} = {8^x}.\frac{1}{{{2^7}}} \Rightarrow x = 5

    Mặt khác {\log _2}45;{\log _2}y;{\log _2}x theo thứ tự lập thành một cấp số cộng nên

    \begin{matrix} {\log _2}y = \dfrac{{{{\log }_2}45 + {{\log }_2}x}}{2} \hfill \\ \Leftrightarrow {\log _2}y = \dfrac{{{{\log }_2}45 + {{\log }_2}5}}{2} \hfill \\ \Leftrightarrow {\log _2}y = {\log _2}\sqrt {255} \Rightarrow y = 15 \hfill \\ \end{matrix}

  • Câu 14: Nhận biết
    Biến đổi biểu thức

    Với a và b là hai số thực dương tùy ý thì \log \left( {a{b^2}} ight) bằng:

    Hướng dẫn:

    Ta có: \log \left( {a{b^2}} ight) = \log a + \log {b^2} = \log a + 2\log b

  • Câu 15: Vận dụng
    Tính

    Gọi x_1, x_2 là 2 nghiệm của phương trình {\log _3}\left( {{x^2} - x - 5} ight) = {\log _3}\left( {2x + 5} ight).

    Khi đó \left| {{x_1} - {x_2}} ight| bằng:

    Hướng dẫn:

     Ta có: {\log _3}\left( {{x^2} - x - 5} ight) = {\log _3}\left( {2x + 5} ight) \Leftrightarrow \left\{ \begin{gathered} 2{\text{x}} + 5 > 0 \hfill \\ {x^2} - x - 5 = 2x + 5 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > - \frac{5}{2} \hfill \\ \left[ \begin{gathered} x = 5 \hfill \\ x = - 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 5 \hfill \\ x = - 2 \hfill \\ \end{gathered} ight.

    Suy ra \left| {{x_1} - {x_2}} ight| =|5-(-2)|=|5+2|=7. 

  • Câu 16: Nhận biết
    Tìm n

    Biết rằng \sqrt x .\sqrt[3]{{{x^2}.\sqrt x }} = {x^n} với x > 0. Tìm n?

    Hướng dẫn:

     Ta có:

    \begin{matrix} \sqrt x .\sqrt[3]{{{x^2}.\sqrt x }} \hfill \\ = {x^{\frac{1}{2}}}.\sqrt[3]{{{x^2}.{x^{\frac{1}{2}}}}} = {x^{\frac{1}{2}}}.\sqrt[3]{{{x^{\frac{5}{2}}}}} \hfill \\ = {x^{\frac{1}{2}}}.{x^{\frac{5}{6}}} = {x^{\frac{1}{2} + \frac{5}{6}}} = {x^{\frac{4}{3}}} \hfill \\ \end{matrix}

    Vậy n = \frac{4}{3}

  • Câu 17: Vận dụng
    Tính giá trị của hàm số tại một điểm

    Biết đồ thị hàm số y = f\left( x ight) đối xứng với đồ thị hàm số y = {\log _a}x;{\text{ }}\left( {0 < a e 1} ight) qua điểm I\left( {2;2} ight). Giá trị của f\left( {4 - {a^{2018}}} ight) là:

    Hướng dẫn:

    Gọi M\left( {x;{{\log }_a}x} ight) là điểm thuộc đồ thị hàm số y = {\log _a}x thì điểm đối xứng với M qua I là M'\left( {4 - x;4 - {{\log }_a}x} ight) thuộc đồ thị hàm số y = f\left( x ight)

    => f\left( {4 - x} ight) = 4 - {\log _a}x \Rightarrow f\left( {4 - {a^{2018}}} ight) = 4 - {\log _a}^{2018} = - 2014

  • Câu 18: Vận dụng
    Tìm nghiệm nguyên MIN

    Nghiệm nguyên nhỏ nhất của bất phương trình {\log _x}3 - {\log _{\frac{x}{3}}}3 < 0  là:

    x=4 || X=4|| x bằng 4

    Đáp án là:

    Nghiệm nguyên nhỏ nhất của bất phương trình {\log _x}3 - {\log _{\frac{x}{3}}}3 < 0  là:

    x=4 || X=4|| x bằng 4

    Theo bài toán, ta xét điều kiện của BPT là: x > 0;x e 1;x e 3.

    Ta có: {\log _x}3 - {\log _{\frac{x}{3}}}3 < 0 \Leftrightarrow \frac{{ - 1}}{{{{\log }_3}x.\left( {{{\log }_3}x - 1} ight)}} < 0

    \Leftrightarrow \left[ \begin{gathered} {\log _3}x < 0 \hfill \\ {\log _3}x > 1 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} 0 < x < 1 \hfill \\ x > 3 \hfill \\ \end{gathered} ight.

  • Câu 19: Vận dụng
    Tìm số các chữ số

    Số {20181991^{20192020}} có bao nhiêu chữ số?

    Gợi ý:

     Số các chữ số của {a^m} là \left[ {\log {a^m}} ight] + 1

    Hướng dẫn:

     Ta có:

    \begin{matrix} \left[ {\log {{20181991}^{20192020}}} ight] + 1 \hfill \\ = \left[ {20192020\log 20182019} ight] + 1 \hfill \\ = 147501991 + 1 = 147501992 \hfill \\ \end{matrix}

  • Câu 20: Thông hiểu
    Viết biểu thức dưới dạng lũy thừa với số mũ hữu tỉ

    Cho a là một số dương, biểu thức {a^{\frac{2}{3}}}.\sqrt a viết dưới dạng lũy thừa với số mũ hữu tỉ là:

    Hướng dẫn:

    Ta có: {a^{\frac{2}{3}}}.\sqrt a = {a^{\frac{2}{3}}}.{a^{\frac{1}{2}}} = {a^{\frac{7}{6}}}

  • Câu 21: Nhận biết
    Mệnh đề nào sau đây là đúng

    Cho biểu thức P = \sqrt {x.\sqrt[3]{{{x^2}.\sqrt {{x^3}} }}} với x > 0. Mệnh đề nào sau đây là đúng?

    Hướng dẫn:

     Ta có: 

    \begin{matrix} P = \sqrt {x.\sqrt[3]{{{x^2}.\sqrt {{x^3}} }}} \hfill \\ P = \sqrt {x.\sqrt[3]{{{x^{\frac{7}{2}}}}}} \hfill \\ P = \sqrt {x.{x^{\frac{7}{6}}}} \hfill \\ P = \sqrt {{x^{\frac{{13}}{6}}}} = {x^{\frac{{13}}{{12}}}} \hfill \\ \end{matrix}

  • Câu 22: Vận dụng
    Tìm nghiệm bé nhất

    Nghiệm bé nhất của phương trình {\log _2}^3x - 2{\log ^2}_2x = {\log _2}x - 2 là: 

    Hướng dẫn:

     TXĐ: x>0

    PT \Leftrightarrow {\log _2}^3x - 2{\log _2}^2x = {\log _2}x - 2 

    \Leftrightarrow {\log _2}^3x - 2{\log _2}^2x - {\log _2}x + 2 = 0

    \Leftrightarrow {\log _2}^3x - {\log _2}x - 2{\log _2}^2x + 2 = 0

    \Leftrightarrow {\log _2}x({\log ^2}_2x - 1) - 2({\log ^2}_2x - 1) = 0

    \Leftrightarrow ({\log ^2}_2x - 1)({\log _2}x - 2) = 0 \Leftrightarrow \left[ \begin{gathered} {\log ^2}_2x - 1 = 0 \hfill \\ {\log _2}x - 2 = 0 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} {\log _2}x = 1 \hfill \\ {\log _2}x = - 1 \hfill \\ {\log _2}x = 2 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 2 \hfill \\ x = \frac{1}{2} \hfill \\ x = 4 \hfill \\ \end{gathered} ight.

    \Rightarrow x = \frac{1}{2} là nghiệm nhỏ nhất.

  • Câu 23: Thông hiểu
    Tính đạo hàm của hàm số

    Tính đạo hàm của hàm số y = {\log _9}\left( {{x^2} + 1} ight)

    Hướng dẫn:

    Ta có:

    y' = \left[ {{{\log }_9}\left( {{x^2} + 1} ight)} ight]' = \frac{{2x}}{{\left( {{x^2} + 1} ight)\ln {3^2}}} = \frac{{2x}}{{\left( {{x^2} + 1} ight).2.\ln 3}} = \frac{x}{{\left( {{x^2} + 1} ight)\ln 3}}

  • Câu 24: Thông hiểu
    Biến đổi biểu thức

    Viết biểu thức Q = \sqrt x .\sqrt[3]{x}.\sqrt[6]{{{x^5}}} với x > 0 dưới dạng lũy thừa với số mũ hữu tỉ?

    Hướng dẫn:

    Ta có:

    Q = \sqrt x .\sqrt[3]{x}.\sqrt[6]{{{x^5}}} = {x^{\frac{1}{2}}}.{x^{\frac{1}{3}}}.{x^{\frac{5}{6}}} = {x^{\frac{1}{2} + \frac{1}{3} + \frac{5}{6}}} = {x^{\frac{5}{3}}}

  • Câu 25: Thông hiểu
    Tìm tập xác định của hàm số logarit

    Tìm tập xác định của hàm số {\log _{\frac{1}{2}}}\left( {{x^2} - 3x + 2} ight)

    Hướng dẫn:

    Điều kiện xác định {x^2} - 3x + 2 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x < 1} \\ {x > 2} \end{array}} ight.

    => Tập xác định của hàm số là D = \left( { - \infty ;1} ight) \cup \left( {2; + \infty } ight)

  • Câu 26: Nhận biết
    Tìm khẳng định đúng?

    Cho các số thực a và b thỏa mãn 0 < a < 1 < b. Tìm khẳng định đúng?

    Hướng dẫn:

     Xét tính đúng sai của từng đáp án như sau

    Ta có {\log _a}b < {\log _a}1 = 0 (vì 0 < a < 1;b > 1) => {\log _a}b < 0 => {\log _a}b < 0 đúng

    Vì a < b \Rightarrow \ln a < \ln b

    => \ln a > \ln b B sai

    Vì \left\{ {\begin{array}{*{20}{c}} {0 < 0,5 < 1} \\ {a < b} \end{array}} ight. \Rightarrow {\left( {0,5} ight)^a} > {\left( {0,5} ight)^b} => {\left( {0,5} ight)^a} < {\left( {0,5} ight)^b} Sai

    Ta có: \left\{ {\begin{array}{*{20}{c}} {2 > 1} \\ {a < b} \end{array}} ight. \Rightarrow {2^a} < {2^b}=> {2^a} > {2^b} sai

  • Câu 27: Vận dụng
    Đạo hàm của hàm số trên khoảng

    Tìm đạo hàm của hàm số y = \sqrt[3]{{{{\left( {1 - 3x} ight)}^5}}} trên khoảng \left( { - \infty ;\frac{1}{3}} ight)

    Hướng dẫn:

    Với điều kiện x < \frac{1}{3} ta có: y = \sqrt[3]{{{{\left( {1 - 3x} ight)}^5}}} = {\left( {1 - 3x} ight)^{\frac{5}{3}}}. Khi đó:

    => y' = - 5{\left( {1 - 3x} ight)^{\frac{2}{3}}}

  • Câu 28: Nhận biết
    Tập xác định của hàm số f(x)

    Tập xác định của hàm số f\left( x ight) = {\left( {{x^2} - 1} ight)^{ - 2}} là:

    Hướng dẫn:

    Hàm số f\left( x ight) = {\left( {{x^2} - 1} ight)^{ - 2}} xác định khi {x^2} - 1 e 0 \Rightarrow x e \pm 1

    Vậy tập xác định của hàm số là D = \mathbb{R}\backslash \left\{ { \pm 1} ight\}

  • Câu 29: Vận dụng
    Tính giá trị biểu thức T = m - n

    Cho x > 0;y > 0. Viết biểu thức {x^{\frac{4}{5}}}.\sqrt[6]{{{x^5}\sqrt x }} = {x^m} và {y^{\frac{4}{5}}}:\sqrt[6]{{{y^5}\sqrt y }} = {y^n}. Tính T = m - n

    Hướng dẫn:

    Ta có:

    \left\{ {\begin{array}{*{20}{c}} {{{\left( {{x^m}} ight)}^6} = {x^{\frac{{24}}{5}}}.{x^5}.{x^{\frac{1}{2}}} = {x^{\frac{{103}}{{10}}}} \Rightarrow m = \dfrac{{103}}{{60}}} \\ {{{\left( {{y^n}} ight)}^6} = {y^{\frac{{24}}{5}}}:\left( {{y^5}.{y^{\frac{1}{2}}}} ight) = {y^{ - \frac{7}{{10}}}} \Rightarrow n = - \dfrac{7}{{60}}} \end{array}} ight. \Rightarrow T = m - n = \frac{{11}}{6}

  • Câu 30: Thông hiểu
    Giải PT

    PT {\log _4}\left( {{{\log }_2}x} ight) + {\log _2}\left( {{{\log }_4}x} ight) = 2 có nghiệm là?

    Hướng dẫn:

     PT \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ {\log _2}x > 0 \hfill \\ {\log _4}x > 0 \hfill \\ {\log _{{2^2}}}\left( {{{\log }_2}x} ight) + {\log _2}\left( {{{\log }_{{2^2}}}x} ight) = 2 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 1 \hfill \\ \frac{1}{2}{\log _2}\left( {{{\log }_2}x} ight) + {\log _2}\left( {\frac{1}{2}{{\log }_2}x} ight) = 2 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 1 \hfill \\ \frac{1}{2}{\log _2}\left( {{{\log }_2}x} ight) + {\log _2}\frac{1}{2} + {\log _2}\left( {{{\log }_2}x} ight) = 2 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 1 \hfill \\ \frac{3}{2}{\log _2}\left( {{{\log }_2}x} ight) - 1 = 2 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 1 \hfill \\ {\log _2}\left( {{{\log }_2}x} ight) = 2 \hfill \\ \end{gathered} ight. \Rightarrow \left\{ \begin{gathered} x > 1 \hfill \\ {\log _2}x = 4 \hfill \\ \end{gathered} ight.

    \Rightarrow \left\{ \begin{gathered} x > 1 \hfill \\ x = 16 \hfill \\ \end{gathered} ight. \Rightarrow x = 16

    Vậy PT có nghiệm là x=16.

0/30
30 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (30%):
    2/3
  • Thông hiểu (30%):
    2/3
  • Vận dụng (40%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 4 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập