Gọi Đ là số các đỉnh, M là số các mặt, C là số các cạnh của một hình đa diện bất kỳ. Mệnh đề nào sau đây là đúng?
Xét hình đa diện là một hình bất kì, ví dụ lấy đa diện là hình tứ diện thì ta có số đỉnh, mặt và cạnh lần lượt là:
Đ=4; M=4; C=6
Gọi Đ là số các đỉnh, M là số các mặt, C là số các cạnh của một hình đa diện bất kỳ. Mệnh đề nào sau đây là đúng?
Xét hình đa diện là một hình bất kì, ví dụ lấy đa diện là hình tứ diện thì ta có số đỉnh, mặt và cạnh lần lượt là:
Đ=4; M=4; C=6
Cho các hình sau:
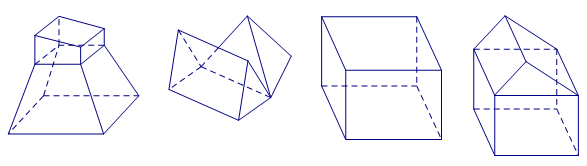
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là:
Các hình đa diện là:
 ;
;  ;
; 
Cho một hình đa diện. Trong các khẳng định sau, khẳng định nào sai?
Áp dụng định nghĩa hình đa diện, ta có:
“Hình đa diện (còn gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác, gọi là các mặt của hình đa diện, thỏa mãn các tính chất sau:
TC1: Hai mặt phân biệt chỉ có thể hoặc không giao nhau hoặc có một đỉnh chung, hoặc có một cạnh chung.
TC2: Mỗi cạnh thuộc một mặt là cạnh cung của đúng hai mặt.
TC3: Cho hai mặt S và S’, luôn tồn tại một dãy các mặt sao cho
trùng với
trùng với S’ và bất kì hai mặt nào cũng đều có một cạnh chung.
Các đỉnh, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.”
Ta thấy ngoai trừ "Mỗi cạnh là cạnh chung của ít nhất ba mặt" các đáp án còn lại đều đúng dựa vào khái niệm hình đa diện.
Cho khối tứ diện ![]() . Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mp
. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mp ![]() và
và ![]() , ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?
, ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?
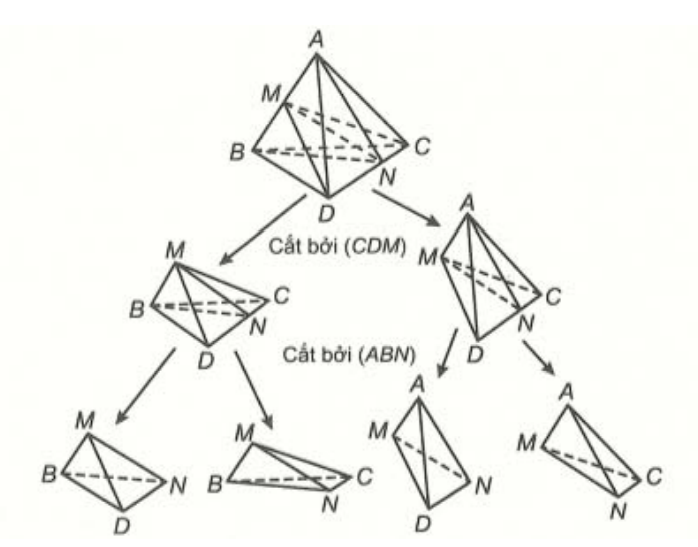
Dựa vào hình vẽ, ta thấy hai mặt phẳng (CDM) và (ABN) chia khối tứ diện ABCD thành bốn khối tứ diện:
Cho các hình sau: 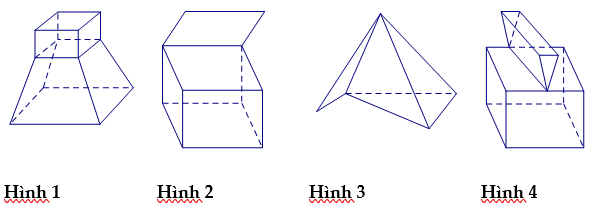
Mỗi hình sau gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
Áp dụng định nghĩa hình đa diện, ta có:
“Hình đa diện (còn gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác, gọi là các mặt của hình đa diện, thỏa mãn các tính chất sau:
TC1: Hai mặt phân biệt chỉ có thể hoặc không giao nhau hoặc có một đỉnh chung, hoặc có một cạnh chung.
TC2: Mỗi cạnh thuộc một mặt là cạnh cung của đúng hai mặt.
TC3: Cho hai mặt S và S’, luôn tồn tại một dãy các mặt sao cho trùng với trùng với S’ và bất kì hai mặt
nào
cũng đều có một cạnh chung.
Các đỉnh, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.”
Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng?
Hình hộp đứng có đáy là hình thoi (không phải là hình chữ nhật) có 3 mặt phẳng đối xứng bao gồm:
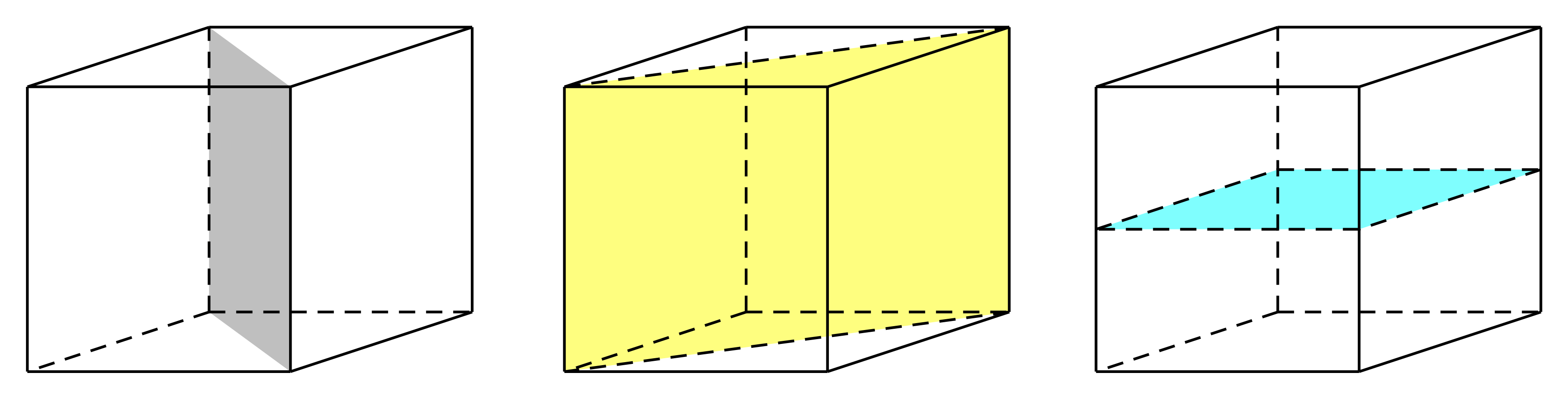
- Hai mặt phẳng chứa đường chéo của đáy và vuông góc với đáy.
- Một mặt phẳng là mặt phẳng trung trực của cạnh bên.
Vật thể nào trong các vật thể sau không phải là khối đa diện?
Vì đáp án đã vi phạm tính chất sau:
Mỗi cạnh của miền đa giác nào cũng là cạnh chung của đúng hai miền đa giác
Mặt phẳng (AB'C') chia khối lăng trụ ABC.A'B'C' thành các khối đa diện nào ?

Dựa vào hình vẽ, ta thấy mặt phẳng (AB'C') chia khối lăng trụ ABC.A'B'C' thành khối chóp tam giác A.A'B'C' và khối chóp tứ giác A.BCC'B'.
Tổng diện tích tất cả các mặt của hình tứ diện đều cạnh a bằng là?
Tứ diện có 4 mặt đều là tam giác đều nên để tính tổng diện tích tất cả các mặt ta chỉ cần tính diện tích 1 mặt (1 mặt là tam giác đều), sau đó đem nhân với 4.
Diện tích 1 mặt của tứ diện đều là diện tích của 1 tam giác đều cạnh a là:
Tổng diện tích tất cả các mặt của hình tứ diện đều cạnh a bằng:
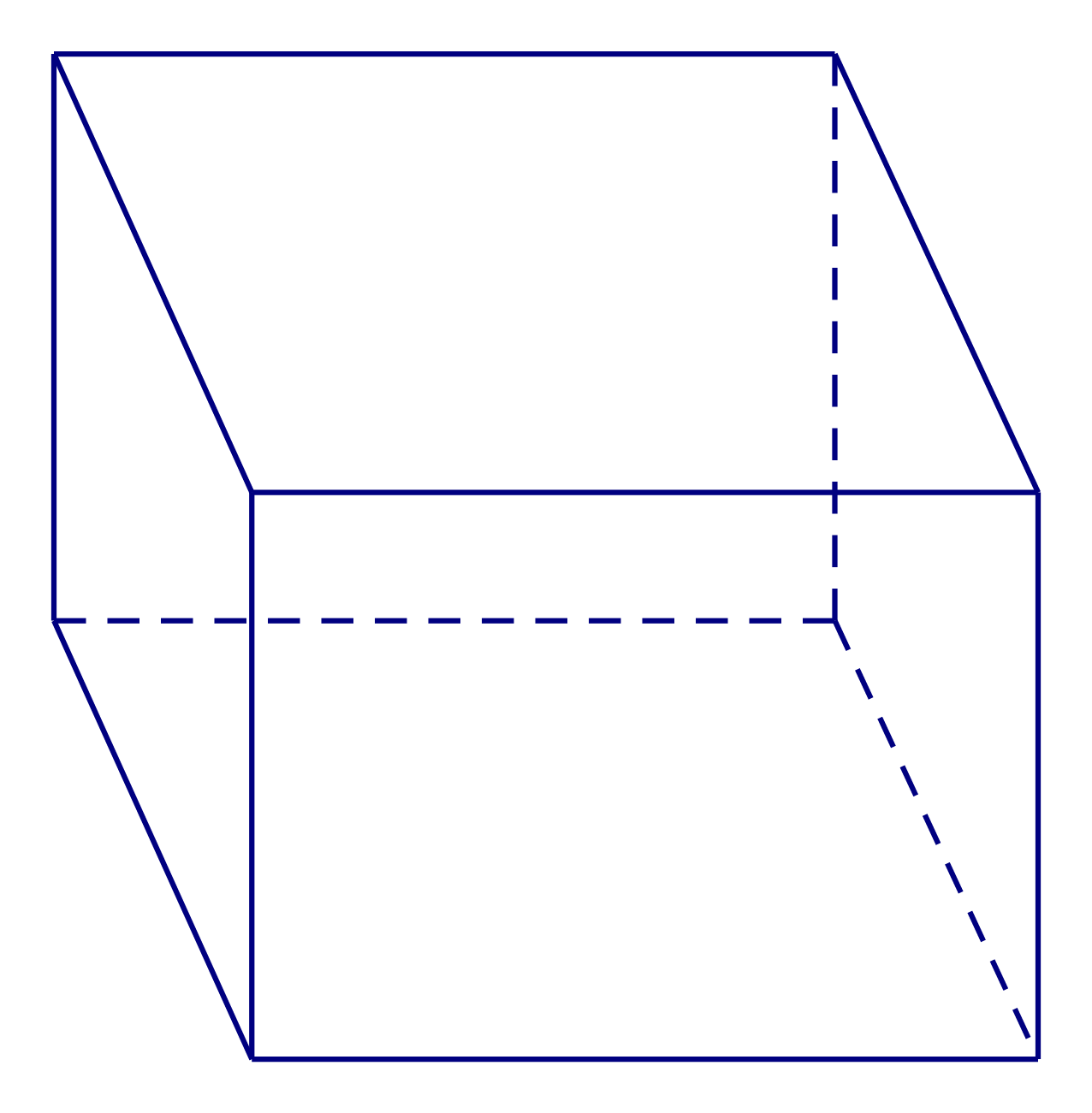
Hình đa diện trong hình vẽ dưới đây có bao nhiêu mặt ?
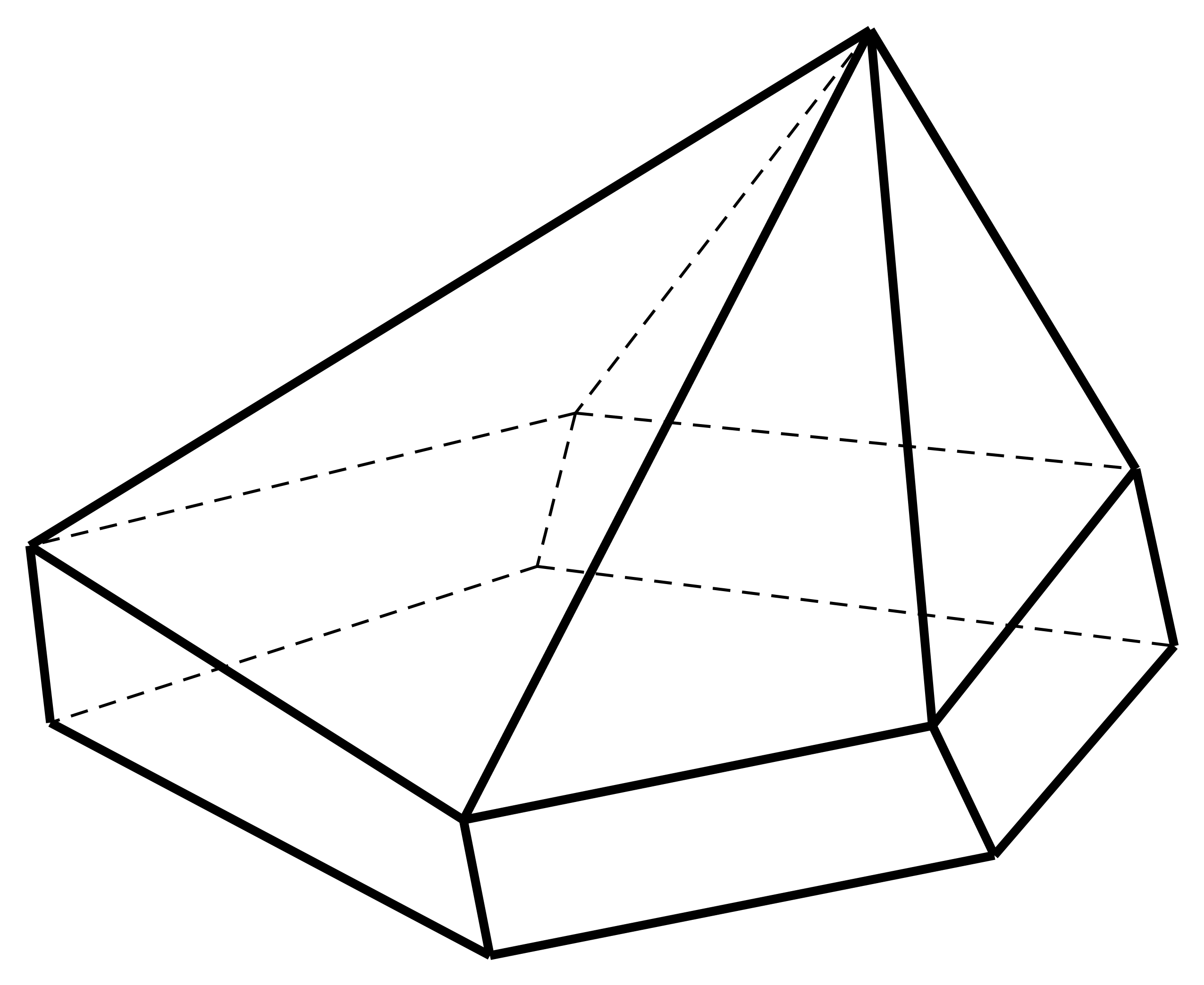
Quan sát hình vẽ và đếm các mặt xung quanh, chú ý cả những mặt được vẽ bằng nét đứt, không nhìn thấy được.
Tính tổng số đo các góc ở tất cả các mặt của hình chóp ngũ giác?
Tính tổng số đo của các góc ở từng mặt sau đó cộng tổng lại ta tổng số đo của tất cả các góc trong hình chóp ngũ giác.
Hình chóp ngũ giác có mặt đáy là hình ngũ giác, có tổng số đo các góc là:
và 5 mặt bên, mỗi mặt bên là một tam giác có số đo các góc là .
Do đó tổng số đo tất cả các góc của hình chóp ngũ giác là:
Cho hình chóp 22 cạnh. Tính số mặt của hình chóp đó?
Tính số cạnh đáy trước, sau đó áp dụng công thức tổng số mặt bằng số mặt bên cộng mặt đáy.
Gọi số cạnh đáy là với
Đáy của chóp là
– giác.
Ứng với mỗi đỉnh của đáy của 1 cạnh nối đỉnh của hình chóp với đỉnh của chóp.
Suy ra hình chóp có tổng số cạnh là .
Theo đề bài, hình chóp có 22 cạnh nên ta được (TMĐK)
Do đó, hình chóp có đáy là 11 – giác.
Do đó chóp có 11 mặt bên cộng 1 đáy.
Vậy hình chóp có tổng 12 mặt.
Trong các mệnh đề sau, mệnh đề nào đúng?
Xét các đáp án, ta có:
- A Đúng: Ta chứng minh như sau:
Gọi M1 là môt mặt khối đa diện, M1 là đa giác nên có ít nhất 3 cạnh c1; c2; c3.
M2 chung cạnh c1 với M1(M2≠M1) , M3 chung cạnh c2 với M1(M3≠M1)
Vì c1∈M3⇒M2≠M3. Gọi M4 là mặt có chung cạnh c3 với M1(M4≠M1)
Vì M4 không chứa c1, c2 nên M4 khác M2 và M3. Do đó khối đa diện có ít nhất 4 mặt ⇒ mỗi hình đa giác có ít nhất 4 đỉnh.
- B Sai.
- C Sai: Ví dụ như hình chóp tam giác có 4 đỉnh nhưng có 6 cạnh.
- D Sai: Lấy ví dụ là hình chóp tam giác có 4 mặt nhưng có 6 cạnh
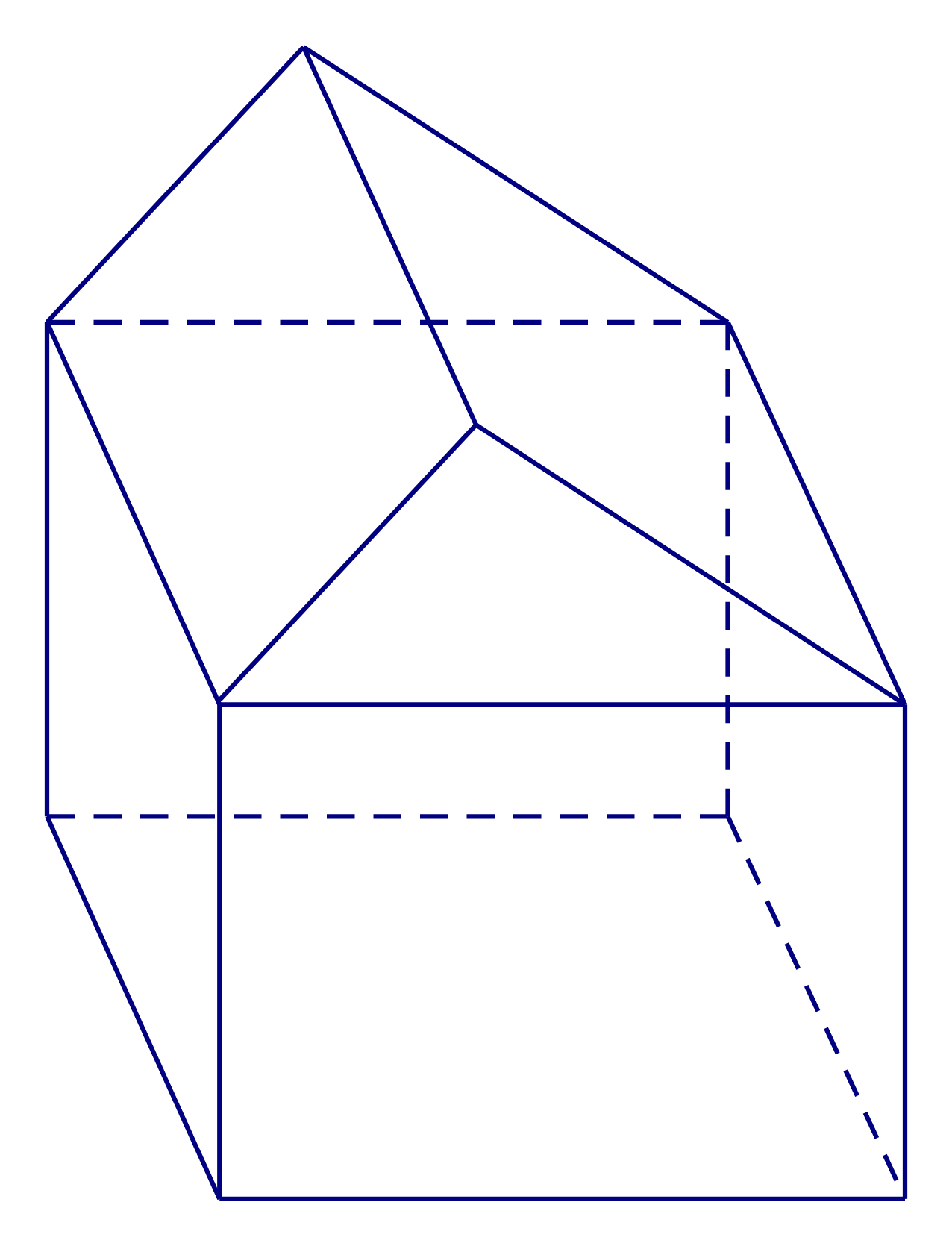
Hình đa diện trong hình vẽ dưới đây có bao nhiêu mặt ?
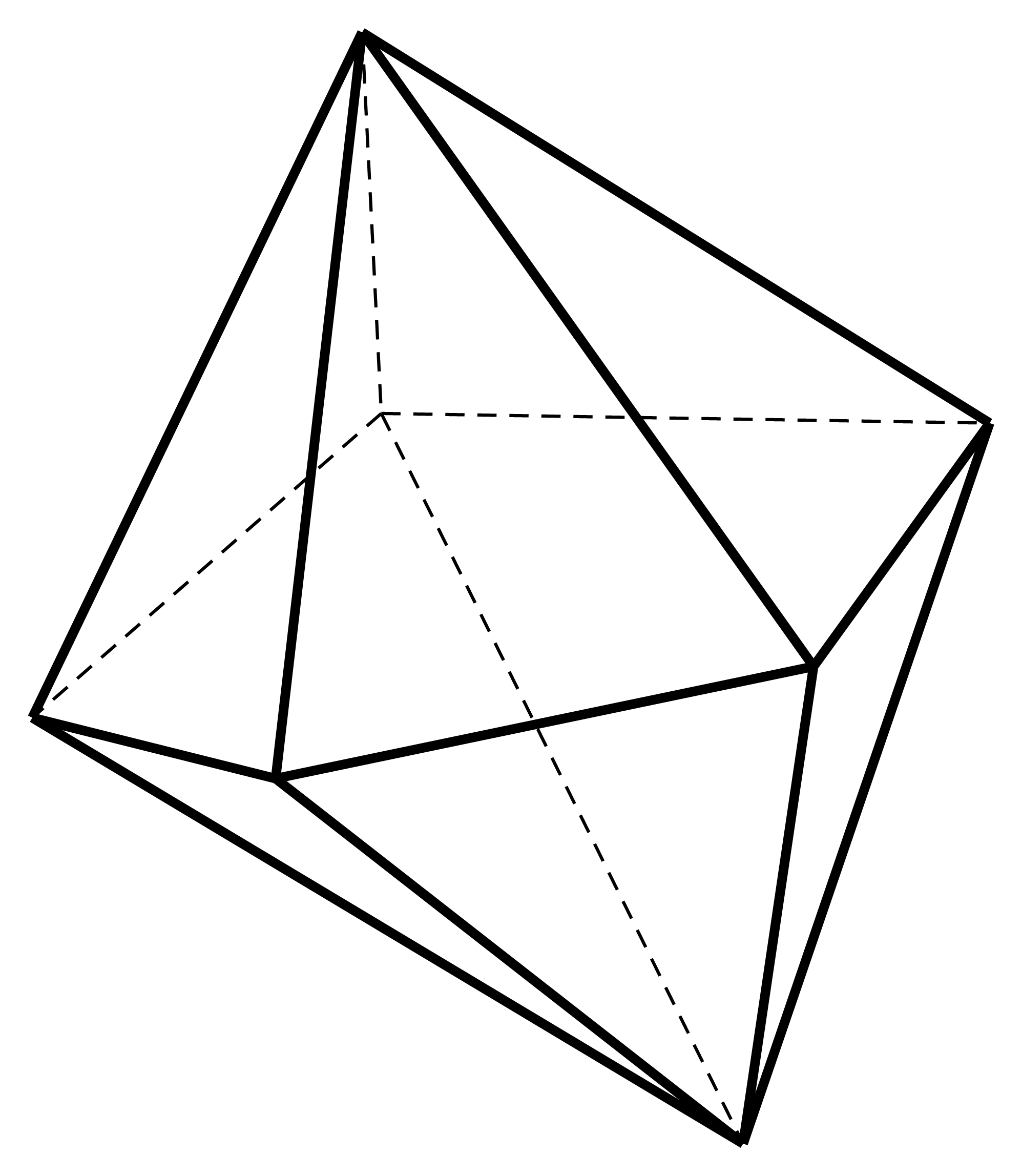
Quan sát hình vẽ và đếm các mặt xung quanh, chú ý cả những mặt được vẽ bằng nét đứt, không nhìn thấy được.
Trong các lăng trụ sau, lăng trụ nào không nội tiếp được trong một mặt cầu?
Để xét xem các lăng trụ có nội tiếp mặt cầu được hay không, ta sẽ xét các mặt đáy của lăng trụ đó xem có phải là hình nội tiếp được đường tròn không.
Nếu lăng trụ có đáy là tứ giác nội tiếp được đường tròn thì lăng trụ đó sẽ nội tiếp được mặt cầu.
Từ đây, ta sẽ xét 1 số tứ giác nội tiếp được đường tròn là: hình vuông, hình chữ nhật, hình thang cân,…
Các khối lập phương đen và trắng xếp chồng lên nhau xen kẽ màu tạo thành một khối rubik ![]() (như hình vẽ).
(như hình vẽ).
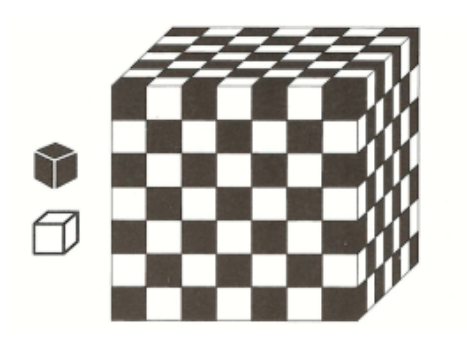
Gọi ![]() là số khối lập phương nhỏ màu đen,
là số khối lập phương nhỏ màu đen, ![]() là số khối lập phương nhỏ màu trắng. Giá trị
là số khối lập phương nhỏ màu trắng. Giá trị ![]() là?
là?
Có 7 lớp hình vuông xếp chồng lên nhau. Mỗi lớp có khối nhỏ.
Ta thấy hai lớp dưới đáy, một khối đen chồng lên một khối trắng (hay ngược lại) nên số lượng khối đen và trắng bằng nhau.
Tương tự 6 lớp bên dưới cũng có số lượng khối đen trắng bằng nhau.
Ta xét lớp trên cùng có khối màu đen và có
khối màu trắng
.
Một hình lăng trụ có 2024 mặt. Hỏi hình lăng trụ đó có tất cả bao nhiêu cạnh?
Áp dụng hệ thức Euler có: Đ + M = C + 2
Gọi số cạnh của 1 đáy hình lăng tụ là cạnh, nên số cạnh đáy của hình lăng trụ (2 mặt đáy ) là
cạnh
Số cạnh bên là cạnh.
=> Tổng số cạnh của lăng trụ là cạnh.
Mặt khác, ta lại có Đ + M = C + 2 (Euler)
Nên suy ra:
Vậy ta tính được số cạnh của hình lăng trụ là (cạnh)
Khối lăng trụ ngũ giác có bao nhiêu cạnh?
Khối lăng trụ ngũ giác có số cạnh của một mặt đáy là 5 cạnh, số cạnh bên là 5 cạnh
Số cạnh của khối lăng trụ ngũ giác là: 2.5 + 5 =15 cạnh.
Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
Hình hộp chữ nhật (không là hình lập phương) có các mặt phẳng đối xứng là các mặt các mặt phẳng trung trực của các cặp cạnh đối.
Gọi ![]() lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Mệnh đề nào sau đây là đúng?
lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Mệnh đề nào sau đây là đúng?
Khối tứ diện đều có 3 trục đối xứng (đi qua trung điểm của các cặp cạnh đối diện).
Khối chóp tứ giác đều có 1 trục đối xứng (đi qua đỉnh và tâm của mặt tứ giác).
Khối lập phương có 9 trục đối xứng
(Loại 1: đi qua tâm của các mặt đối diện ;
Loại 2: đi qua trung điểm các cặp cạnh đối diện).
