Cho hàm số ![]() liên tục trên đoạn
liên tục trên đoạn ![]() . Gọi
. Gọi ![]() là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() . Thể tích khối tròn xoay tạo thành khi quay
. Thể tích khối tròn xoay tạo thành khi quay ![]() quanh trục hoành được tính theo công thức:
quanh trục hoành được tính theo công thức:
Thể tích của khối tròn xoay cần tính là:
Cho hàm số ![]() liên tục trên đoạn
liên tục trên đoạn ![]() . Gọi
. Gọi ![]() là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() . Thể tích khối tròn xoay tạo thành khi quay
. Thể tích khối tròn xoay tạo thành khi quay ![]() quanh trục hoành được tính theo công thức:
quanh trục hoành được tính theo công thức:
Thể tích của khối tròn xoay cần tính là:
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số ![]() , trục hoành và các đường thẳng
, trục hoành và các đường thẳng ![]()
Diện tích S của hình phẳng trên là:
Ta có:
=>
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ![]() là:
là:
Phương trình hoành độ giao điểm 2 đồ thị là:
Diện tích cần tìm là:
Một khu vườn được quy hoạch để trồng hoa hồng được giới hạn bởi parabol và nửa đường tròn bán kính (phần tô màu trong hình vẽ). Hỏi số tiền tối thiểu để trồng kín hoa trong vườn? Biết mỗi mét vuông trồng hoa cần ít nhất 300.000 đồng.
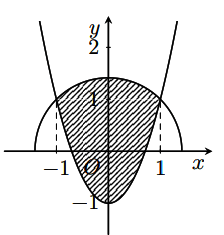
Nửa đường tròn có phương trình
Xét parabol có trục đối xứng
nên có phương trình dạng
cắt
tại điểm
=>
cắt
tại điểm
thuộc
=>
Phương trình là:
Diện tích miền phẳng (phần tô màu trong hình là:
Xét đặt
=>
Ta có:
Khi đó ta có:
Số tiền trồng hoa tối thiểu là: đồng
Tốc độ tăng trưởng bán kính của thân cây được tính bằng công thức ![]() , trong đó
, trong đó ![]() là thời gian khảo sát (tính theo năm), là thời điểm đầu khảo sát,
là thời gian khảo sát (tính theo năm), là thời điểm đầu khảo sát, ![]() là bán kính của thân cây tại thời điểm
là bán kính của thân cây tại thời điểm ![]() và
và ![]() . Tính bán kính của thân cây sau 20 năm kể từ lúc bắt đầu khảo sát, biết rằng bán kính cây tại thời điểm bắt đầu khảo sát là 5cm.
. Tính bán kính của thân cây sau 20 năm kể từ lúc bắt đầu khảo sát, biết rằng bán kính cây tại thời điểm bắt đầu khảo sát là 5cm.
Ta có:
Từ giả thiết ta có:
=>
Sau 5 năm bán kính thân cây bằng
Một ô tô xuất phát với vận tốc ![]() sau khi đi được một khoảng thời gian
sau khi đi được một khoảng thời gian ![]() thì bất ngờ phanh gấp với vận tốc
thì bất ngờ phanh gấp với vận tốc ![]() và đi thêm được một khoảng thời gian
và đi thêm được một khoảng thời gian ![]() nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì ô tô đã đi được bao nhiêu mét?
nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì ô tô đã đi được bao nhiêu mét?
Ta có: do đó khi gặp chướng ngại vật vật có vận tốc là
=>
Vật dừng lại khi
Quãng đường vật đi được là
Cho hai quả bóng A, B đều chuyển động thẳng, di chuyển ngược chiều và va chạm với nhau. Sau mỗi va chạm, hai quả bóng nảy ngược lại một đoạn thì dừng hẳn. Tính khoảng cách giữa hai quả bóng sau khi dừng hẳn. Biết sau khi va chạm, quả bóng A này ngược lại với vận tốc ![]() và quả bóng B nảy ngược lại với vận tốc
và quả bóng B nảy ngược lại với vận tốc ![]() .
.
Tính thời gian từng quả bóng chuyển động đến khi dừng hẳn
=> Quãng đường từng quả di chuyển được.
Thời gian quả bóng A chuyển động từ lúc va chạm đến khi dừng hẳn là:
Quãng đường quả bóng A di chuyển được là:
Thời gian quả bóng B chuyển động từ lúc va chạm đến khi dừng hẳn là:
Quãng đường quả bóng B di chuyển được là:
Vậy khoảng cách hai quả bóng sau khi dừng hẳn là
Một ô tô đang chạy đều với vận tốc ![]() thì người lái xe đạp phanh. Từ thời điểm ô tô chuyển động chậm dần đều với vận tốc
thì người lái xe đạp phanh. Từ thời điểm ô tô chuyển động chậm dần đều với vận tốc ![]() . Biết từ khi đạp phanh đến lúc dừng hẳn thì ô tô di chuyển được 56m. Tính giá trị của
. Biết từ khi đạp phanh đến lúc dừng hẳn thì ô tô di chuyển được 56m. Tính giá trị của ![]() ?
?
Khi dừng hẳn
Quãng đường xe đi được từ khi đạp phanh đến lúc dừng hẳn là:
Cho ![]() là hình phẳng giới hạn bởi đường cong
là hình phẳng giới hạn bởi đường cong ![]() và đường thẳng
và đường thẳng ![]() . Tính thể tích
. Tính thể tích ![]() của vật thể tròn xoay do hình phẳng
của vật thể tròn xoay do hình phẳng ![]() quay quanh trục hoành.
quay quanh trục hoành.
Phương trình hoành độ giao điểm là:
Thể tích cần tính là:
Tính diện tích hình phẳng được giới hạn bởi đồ thị ![]() và hai tiếp tuyến của
và hai tiếp tuyến của ![]() tại
tại ![]()
Ta có hình vẽ minh họa như sau:
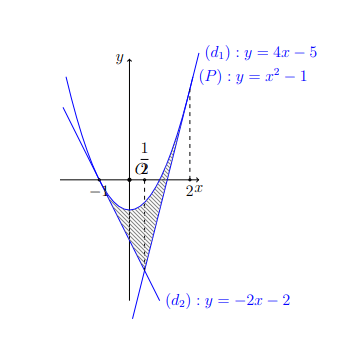
Phương trình tiếp tuyến của (P) tại A(-1;0) là:
Phương trình tiếp tuyến của (P) tại B(2;3) là:
Từ hình vẽ ta suy ra diện tích của hình phẳng cần tìm là:
Một ô tô đang chạy với vận tốc ![]() thì dừng lái đạp phanh. Sau khi đạp phanh, ô tô di chuyển động chậm dần đều với vận tốc
thì dừng lái đạp phanh. Sau khi đạp phanh, ô tô di chuyển động chậm dần đều với vận tốc ![]() , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
, trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
Khi dừng hẳn
Quãng đường xe đi được từ khi đạp phan đến lúc dừng hẳn là:
Gọi (H) là hình phẳng xác định bởi ![]() và trục hoành. Tính thể tích khối tròn xoay khi quay hình (H) quanh trục Ox.
và trục hoành. Tính thể tích khối tròn xoay khi quay hình (H) quanh trục Ox.
Hình vẽ minh họa:
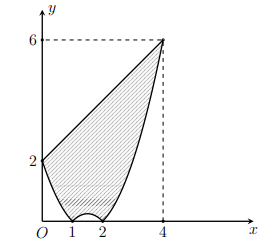
Tọa độ giao điểm của (C) và trục hoành là (1; 0) và (2; 0)
Tọa độ giao điểm của (C) và (D) là (0; 2) và (4; 6)
Dễ thấy
Thể tích cần tìm là:
Cho đường cong (C) ![]() . Xét điểm A có hoành độ dương thuộc (C), tiếp tuyến của (C) tại A tạo với (C) một hình phẳng có diện tích bằng 27. Hoành độ điểm A thuộc khoảng nào dưới đây?
. Xét điểm A có hoành độ dương thuộc (C), tiếp tuyến của (C) tại A tạo với (C) một hình phẳng có diện tích bằng 27. Hoành độ điểm A thuộc khoảng nào dưới đây?
Ta có:
Ta có:
Phương trình tiếp tuyến d của (C) tại A là
Ta có phương trình hoành độ giao điểm d và (C) là:
Gọi S là diện tích của hình phẳng giới hạn bởi tiếp tuyến d và (C).
Ta có:
Tính diện tích hình phẳng giới hạn bởi ![]()
Xét phương trình hoành độ giao điểm ta có:
Diện tích hình phẳng cần tính là:
Một vật chuyển động chậm dần đều với vận tốc ![]() . Hỏi rằng trong
. Hỏi rằng trong ![]() trước khi dừng hẳn vật di chuyển được bao nhiêu mét?
trước khi dừng hẳn vật di chuyển được bao nhiêu mét?
Khi dừng hẳn:
Khi đó trong trước khi dừng hẳn vật di chuyển được:
Viết công thức tính thể tích ![]() của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số
của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số ![]() , trục
, trục ![]() và hai đường thẳng
và hai đường thẳng ![]() xung quanh trục
xung quanh trục ![]() .
.
Thể tích của khối tròn xoay cần tính là:
Một vật chuyển động với vận tốc ban đầu là ![]() và gia tốc
và gia tốc ![]() . Hỏi sau khi chuyển động với gia tốc đó được 2 giây thì vận tốc của vật là bao nhiêu?
. Hỏi sau khi chuyển động với gia tốc đó được 2 giây thì vận tốc của vật là bao nhiêu?
Ta có:
Do khi bắt đầu tăng tốc nên
Vận tốc của vật khi chuyển động với gia tốc đó được là
Thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường ![]() , khi xoay quanh trục
, khi xoay quanh trục ![]() .
.
Phương trình hoành độ giao điểm là:
Gọi là thể tích khối tròn xoay cần tìm ta có:
Đặt
Cho đường tròn ![]() và parabol
và parabol ![]() .
. ![]() cắt
cắt ![]() thành hai phần. Tìm tỉ số diện tích của hai phần đó.
thành hai phần. Tìm tỉ số diện tích của hai phần đó.
Hoành độ giao điểm của (P) và (C) là:
Xét giao điểm thuộc góc phần tư thứ nhất, với
Gọi S2 là phần có diện tích nhỏ hơn, S1 là phần còn lại
Ta có:
Đặt
Khi đó
Diện tích hình tròn
Cho ![]() là miền hình phẳng giới hạn bởi các đường
là miền hình phẳng giới hạn bởi các đường ![]() và đồ thị của hai hàm số
và đồ thị của hai hàm số ![]() . Gọi V là thể tích của vật thể tròn xoay khi quay
. Gọi V là thể tích của vật thể tròn xoay khi quay ![]() quanh Ox. Mệnh đề nào dưới đây đúng?
quanh Ox. Mệnh đề nào dưới đây đúng?
Thể tích của khối tròn xoay cần tính là:
