Thể tích khối đa diện

Bài học Lí thuyết toán 12: Thể tích khối đa diện bao gồm khái niệm về thể tích, một số công thức tính thể tích thường gặp và tỉ số thể tích. Bên cạnh đó là các ví dụ bài tập có lời giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia. Hi vọng các em sẽ ôn tập hiệu quả, hướng đến đạt mục tiêu trong các kì thi lớn sắp tới.

1. Khái niệm về thể tích

Cho khối đa diện $(H)$ . Số dương $V_{(H)}$ được gọi là thể tích của khối đa diện $(H)$ nếu thỏa mãn các tính chất sau:

Nếu $(H)$ là khối lập phương có cạnh bằng 1 thì $V_{(H)} =1$
Nếu hai khối đa diện $(H_1)$ và $(H_2)$ bằng nhau thì $V_{(H_1)} = V_{(H_2)}$
Nếu khối đa diện $(H)$ được phân chia thành hai khối đa diện $(H_1)$ và $(H_2)$ thì: $V_{(H)}= V_{(H_1)} + V_{(H_2)}$

Nhận xét:

$V_{(H)}$ còn được gọi là thể tích của hình đa diện giới hạn khối đa diện $(H)$
Khối lập phương đơn vị là khối lập phương có cạnh bằng 1.

2. Bảng công thức tính thể tích

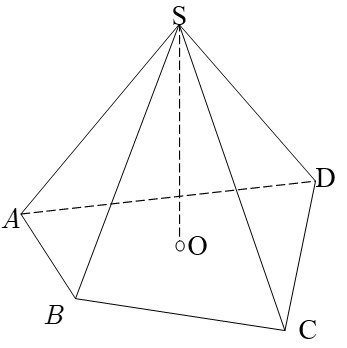
Thể tích khối chóp:

$\boxed{V = \frac{1}{3}B.h}$

Trong đó:

$B$ : Diện tích mặt đáy.
$h$ : Chiều cao của khối chóp.

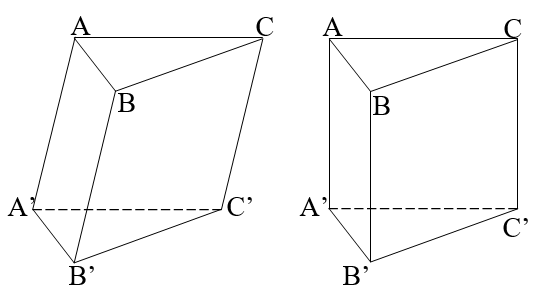
Thể tích khối lăng trụ:

$\boxed{V = B.h}$

$B$ : Diện tích mặt đáy.
$h$ : Chiều cao của khối chóp.

Lưu ý: Lăng trụ đứng có chiều cao cũng là cạnh bên.

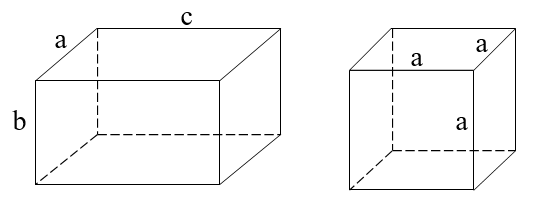
Thể tích hình hộp chữ nhật:

$\boxed{V = a.b.c}$

$\Rightarrow$ Thể tích khối lập phương:

$\boxed{V = {a^3}}$

Hình chóp cụt $ABC.A'B'C'$

$\boxed{V = \frac{h}{3}\left( {B + B' + \sqrt {BB'} } \right)}$

Với $B,B',h$ là diện tích hai đáy và chiều cao.

Ví dụ: Cho $S.ABCD$ là hình chóp đều. Tính thể tích khối chóp $S.ABCD$ biết $AB=a$ , $SA=a$ .

Giải:

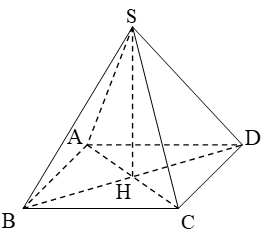
+) Gọi H là hình chiếu của S lên (ABCD)

+) Ta có: $AH = \frac{{a\sqrt 2 }}{2}$

$\Rightarrow SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt 2 }}{2}$

+) Vì $S.ABCD$ là hình chóp đều nên đáy là hình vuông. Ta suy ra diện tích đáy ABCD là: ${S_{ABCD}} = {a^2}$

+) Áp dụng công thức tính thể tích $\Rightarrow {V_{S.ABCD}} = \frac{{{a^3}\sqrt 2 }}{6}$

3. Tỉ số thể tích

Cho khối chóp $S.ABC$ . Trên các cạnh $SA, SB, SC$ lần lượt lấy các điểm $A' , B', C'$ khồng trùng nhau.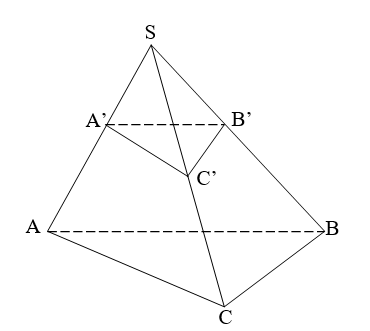

Ta có công thức tính tỉ số thể tích giữa 2 khối chóp $S.ABC$ và $S.A'B'C'$ là:

$\boxed{\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}}$

Ví dụ: Cho hình chóp $S.ABC$ , gọi $M, \, N$ lần lượt là trung điểm của $SA, \, SB$ . Tính tỉ số $\frac{{{V_{S.ABC}}}}{{{V_{S.MNC}}}}$

Giải: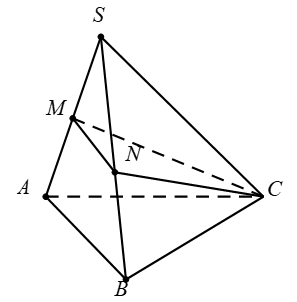

Theo đề bài, áp dụng công thức tính tỉ số thể tích, ta có:

$\frac{{{V_{S.ABC}}}}{{{V_{S.MNC}}}} = \frac{{SA}}{{SM}}.\frac{{SB}}{{SN}} = 4$

Câu trắc nghiệm mã số: 1604,1601,1598, 1595,1593,1171

6 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo

Xóa Gửi bình luận

Toán 12