Giá trị của tham số m sao cho hàm số ![]() nghịch biến trên khoảng (0; 2)?
nghịch biến trên khoảng (0; 2)?
Ta có:
Hàm số nghịch biến trên khoảng (0; 2)
=>
=>
Xét hàm số
Ta có:
=> g(x) đồng biến trên đoạn [0; 2]
Ta có:
Giá trị của tham số m sao cho hàm số ![]() nghịch biến trên khoảng (0; 2)?
nghịch biến trên khoảng (0; 2)?
Ta có:
Hàm số nghịch biến trên khoảng (0; 2)
=>
=>
Xét hàm số
Ta có:
=> g(x) đồng biến trên đoạn [0; 2]
Ta có:
Hàm số y = x3 – 3x2 nghịch biến trên khoảng nào dưới đây?
Ta có:
Theo dấu hiệu nhận biết tính đơn điệu của hàm số, hàm số nghịch biến trên (0; 2)
Cho ![]() hàm số có
hàm số có ![]() . Hàm số
. Hàm số ![]() đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
Xét dấu f’(x) như sau:
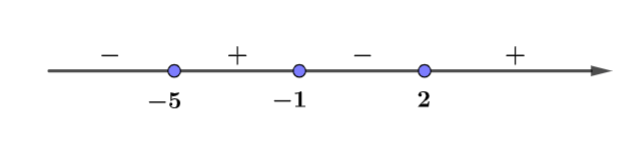
Ta có:
Chọn ta có:
=> là khoảng âm
Khi đó bảng xét dấu của y’ = (f(x2))’ như sau:
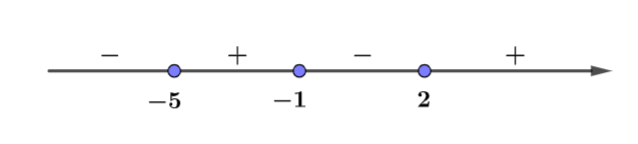
Từ trục xét dấu ta thấy. Hàm số y = f(x2) đồng biến trên (-1; 0)
Gọi P là tập hợp các giá trị nguyên của tham số m để hàm số ![]() đồng biến trên tập xác định của nó. Tổng các phần tử của tập hợp P là:
đồng biến trên tập xác định của nó. Tổng các phần tử của tập hợp P là:
Ta có:
Hàm số đồng biến trên khi và chỉ khi
Kết hợp với điều kiện
=>
=> Tổng P bằng 10
Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng
Ta có y’ = 8x => y’ = 0 => x = 0
=> y’ > 0 => x > 0
=> y’ < 0 => x < 0
Vậy hàm số đồng biến trên khoảng
Trong các hàm số dưới đây, hàm số nào đồng biến trên ![]() ?
?
Hàm số y = x – sinx có tập các định và
Nên hàm số luôn đồng biến trên
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
Xét hàm số ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Ta có:
Ta có bảng xét dấu cho các biểu thức
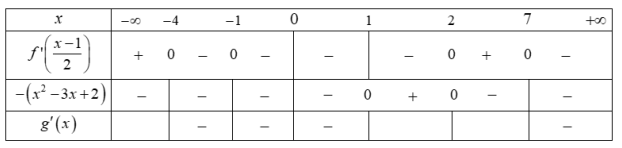
Từ bảng xét dấu ta thấy
Khi đó hàm số nghịch biến
=> Đáp án B sai
Số giá trị nguyên của tham số m để hàm số ![]() đồng biến trên
đồng biến trên ![]() ?
?
Ta có:
Hàm số đồng biến trên khi và chỉ khi
Kết hợp với điều kiện
Vậy có tất cả 5 giá trị của m thỏa mãn điều kiện đề bài.
Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (-1; +∞)
Ta có: . Theo yêu cầu bài toán ta có:
=>
Xét hàm số
Ta có bảng biến thiên như sau:
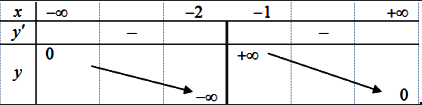
Vậy
Trong các hàm số sau, hàm số nào vừa có khoảng đồng biến vừa có khoảng nghịch biến trên tập xác định của nó. (I) ![]() ; (II)
; (II) ![]() ; (III)
; (III)
(I) Tập xác định
=> (I) không thỏa mãn
(II) Tập xác định
Bảng xét dấu
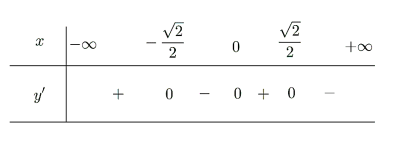
=> (II) thỏa mãn
(III) Tập xác định
=> Hàm số nghịch biến trên tập số thực
=> (III) không thỏa mãn
Cho hàm số y = f(x). Đồ thị của hàm số ![]() như hình bên. Đặt
như hình bên. Đặt ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Xét hàm số
Ta có bảng biến thiên như sau:
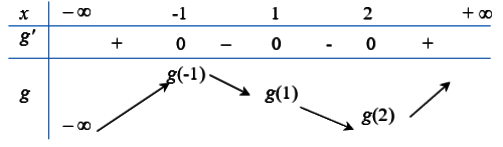
Vậy
Tổng tất cả các giá trị thực của m để hàm số ![]() đồng biến trên R bằng:
đồng biến trên R bằng:
Ta có:
Hàm số đã cho đồng biến trên R khi và chỉ khi
Và dấu bằng xảy ra chỉ tại một số hữu hạn điểm.
Điều kiện cần
Ta thấy phương trình y ‘ = 0 có một nghiệm x = -1 nên để thì y’ không đổi dấu qua khi x = -1 khi đó phương trình y’ = 0 có nghiệm kép là x = -1 (x = -1 không thể laf nghiệm bội 4 của phương trình y’ = 0 vì y’ không chứa số hạng x3)
Ta suy ra được y’’(-1) = 0
=>
Điều kiện đủ:
Với m = - 2 ta có:
=> Hàm số đồng biến trên R
=> m = -2 thỏa mãn điều kiện đề bài.
Với ta có:
=> Hàm số đồng biến trên R
=> thỏa mãn điều kiện đề bài
Vậy là các giá trị cần tìm.
=> Tổng các giá trị thực của m cần tìm thỏa mãn yêu cầu bài toán là
Hàm số y = x4 - 2x2 + 1 đồng biến trên khoảng nào?
Ta có bảng biến thiên như sau:
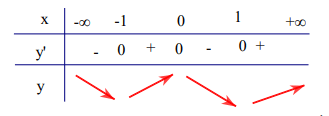
Hàm số y = x4 – 2x2 + 1 đồng biến trên mỗi khoảng (-1; 0) và (1; +∞)
Hàm số nào sau đây đồng biến trên các khoảng (-∞; 2) và (2; +∞)?
Ta có:
Vậy hàm số đồng biến trên các khoảng (-∞; 2) và (2; +∞)
Cho hàm số y = f(x) có đạo hàm ![]() . Hàm số
. Hàm số ![]() đồng biến trên khoảng nào trong các khoảng sau?
đồng biến trên khoảng nào trong các khoảng sau?
Ta có:
Ta có:
Cho g’(x) = 0 =>
Dựa vào f’(x) ta có:
Lập bảng xét dấu như sau:
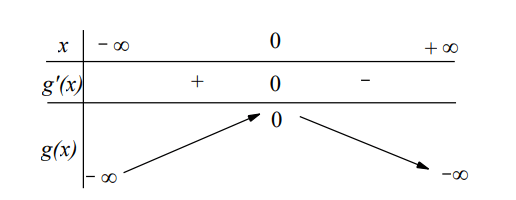
Quan sát bảng xét dấy ta suy ra hàm số đồng biến trên khoảng (2; 4)
Trong các hàm số sau, hàm số nào đồng biến trên ![]() ?
?
Ta có:
Ta có: y’ = 0 chỉ tại x = 1
Vậy đồng biến trên
Kết luận nào sau đây về tính đơn điệu của hàm số ![]() là đúng?
là đúng?
Ta có:
Do đó hàm số nghịch biến trên các khoảng (-∞; 2) và (2; +∞)
Cho hàm số y = f(x) có đạo hàm f’(x) = x2 + 1, ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
Ta có:
f’(x) = x2 + 1 > 0,
=> Hàm số đống biến trên khoảng (-∞; +∞)
Hàm số ![]() nghịch biến trên khoảng nào?
nghịch biến trên khoảng nào?
Ta có:
=> Hàm số nghịch biến trên khoảng (2; 3)
Tìm tập hợp T tất cả các giá trị của tham số thực m để hàm số ![]() nghịch biến trên khoảng (-1; 1)
nghịch biến trên khoảng (-1; 1)
Ta có:
Để hàm số nghịch biến trên khoảng (-1; 1) thì
Ta có y’ = 0 => x = m hoặc x = m + 2
Bảng xét dấu

Từ bảng xét dấu ta thấy để hàm số nghịch biến trên khoảng (-1; 1) thì
