Hình nón có đường sinh ![]() và hợp với đáy góc
và hợp với đáy góc ![]() . Diện tích toàn phần của hình nón bằng:
. Diện tích toàn phần của hình nón bằng:
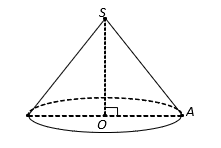
Theo giả thiết, ta có
và
.
Suy ra:
.
Vậy diện tích toàn phần của hình nón bằng: (đvdt).
Hình nón có đường sinh ![]() và hợp với đáy góc
và hợp với đáy góc ![]() . Diện tích toàn phần của hình nón bằng:
. Diện tích toàn phần của hình nón bằng:

Theo giả thiết, ta có
và
.
Suy ra:
.
Vậy diện tích toàn phần của hình nón bằng: (đvdt).
Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chu vi đáy bằng 2a thì thể tích của nó bằng:
Gọi bán kính đáy là R.
Hình trụ có chu vi đáy bằng 2a nên ta có .
Suy ra hình trụ này có đường cao .
Vậy thể tích khối trụ (đvtt).
Cho một chiếc cốc có dạng hình nón cụt và một viên bi có đường kính bằng chiều cao của cốc. Đổ đầy nước rồi thả viên bi vào, ta thấy lượng nước tràn ra bằng một phần ba lượng nước đổ vào cốc lúc ban đầu. Biết viên bi tiếp xúc với đáy cốc và thành cốc. Tìm tỉ số bán kính của miệng cốc và đáy cốc (bỏ qua độ dày của cốc).
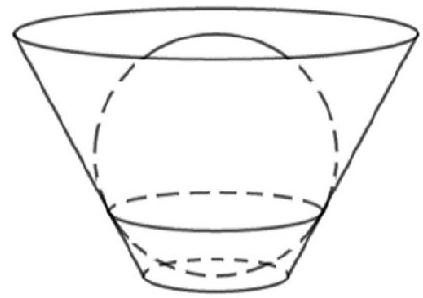
Gọi bán kính viên bi là r; bán kính đáy cốc, miệng cốc lần lượt là . Theo giả thiết thì chiều cao của cốc là
.
Thể tích viên bi là
Thể tích cốc là .
Theo giả thiết thì (1).
Mặt cắt chứa trục của cốc là hình thang cân . Đường tròn tâm
là đường tròn lớn của viên bi, đồng thời là đường tròn nội tiếp hình thang
, tiếp xúc với
lần lượt tại
và tiếp xúc với BB' tại M.
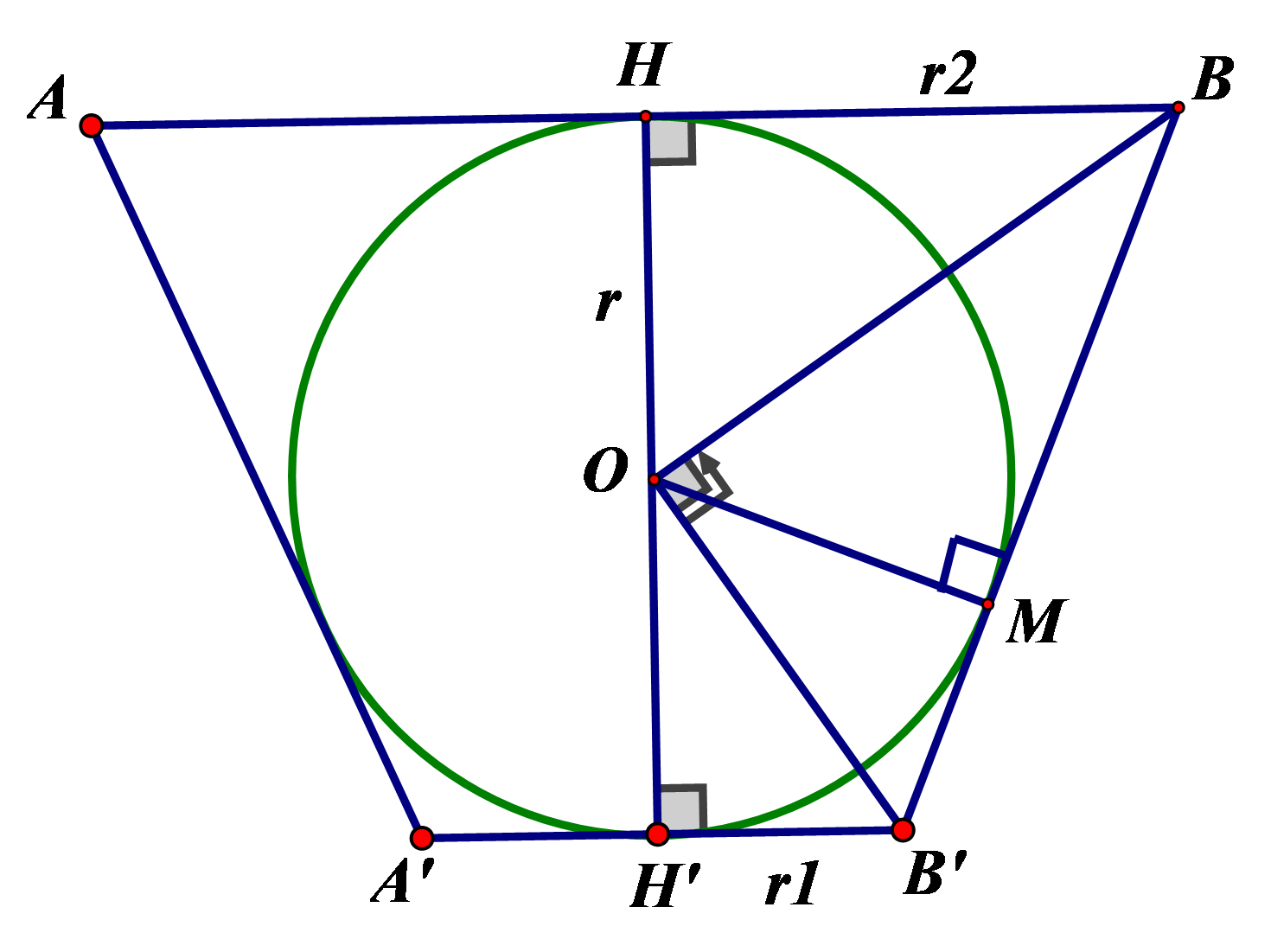
Dễ thấy tam giác BOB' vuông tại O.
Ta có .
Thay (2) vào (1) ta được .
Giải phương trình với điều kiện ta được
.
Xét các mệnh đề:
(I) Tập hợp các đường thẳng d thay đổi nhưng luôn luôn song song và cách đường thẳng ![]() cố định một khoảng không đổi là một mặt trụ.
cố định một khoảng không đổi là một mặt trụ.
(II) Hai điểm A, B cố định. Tập hợp các điểm M trong không gian mà diện tích tam giác MAB không đổi là một mặt trụ.
Trong các mệnh đề trên, mệnh đề nào đúng?
Ta xét về khái niệm Mặt trụ suy ra (I) đúng.
Diện tích tam giác MAB không đổi khi và chỉ khi khoảng cách từ M đến đường thẳng AB không đổi (giả sử bằng R ).
Vậy tập hợp các điểm M là mặt trụ bán kính R và trục là AB.
Vì vậy Mệnh đề (II) cũng đúng.
Bán kính đáy hình trụ bằng 4 cm, chiều cao bằng 6cm. Độ dài đường chéo của thiết diện qua trục bằng:
Thiết diện qua trục của một hình trụ là một hình chữ nhật có hai cạnh lần lượt bằng đường kính đáy và chiều cao của hình trụ.
Vậy hai cạnh của hình chữ nhật là 8 cm và 6 cm.
Do đó độ đài đường chéo:
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng a. Thể tích khối trụ bằng:
Do thiết diện đi qua trục hình trụ nên ta có h=a.
Bán kính đáy . Do đó thể tích khối trụ
(đvtt).
Trong các hình trụ có diện tích toàn phần bằng ![]() thì hình trụ có thể tích lớn nhất là bao nhiêu
thì hình trụ có thể tích lớn nhất là bao nhiêu ![]()
Ta có
Vậy thể tích khối trụ
Ta có:
Bảng biến thiên
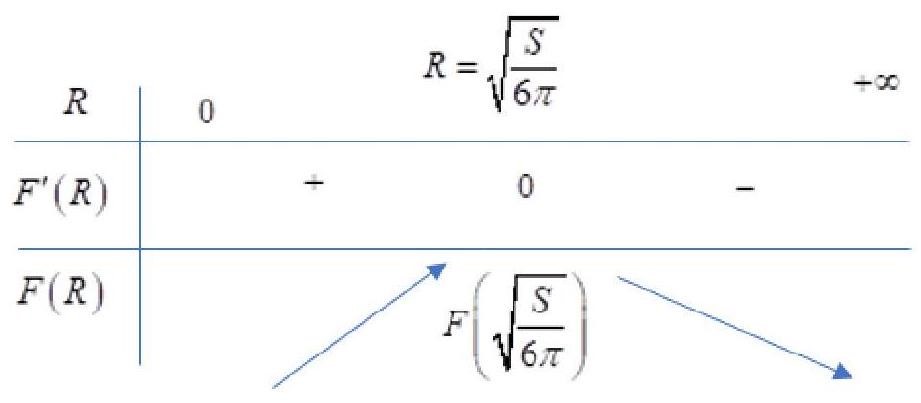
Từ bảng biến thiên ta có
.
Cho hình trụ có O, O' là tâm hai đáy. Xét hình chữ nhật ![]() có A, B cùng thuộc (O) và C, D cùng thuộc (O') sao cho
có A, B cùng thuộc (O) và C, D cùng thuộc (O') sao cho ![]() đồng thời
đồng thời ![]() tạo với mặt phẳng đáy hình trụ góc
tạo với mặt phẳng đáy hình trụ góc ![]() . Thể tích khối trụ bằng
. Thể tích khối trụ bằng
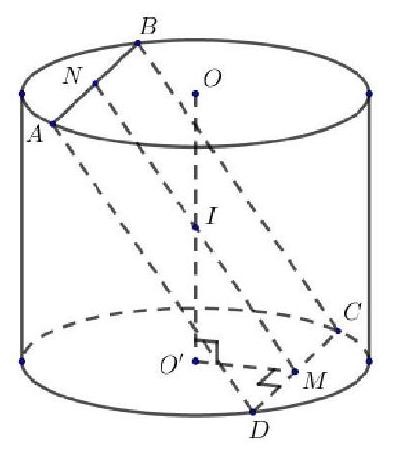
Gọi lần lượt là trung điểm của
và
là trung điểm của
. Suy ra góc giữa mặt phẳng
và mặt phẳng đáy là
.
Ta có .
Xét vuông tại O, ta có:
;
Xét vuông tại M, có
.
Vậy .
Một khối lập phương có cạnh 1m chứa đầy nước. Đặt vào trong khối đó một khối nón có đỉnh trùng với tâm một mặt của lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích lượng nước trào ra ngoài và thể tích lượng nước ban đầu của khối lập phương.
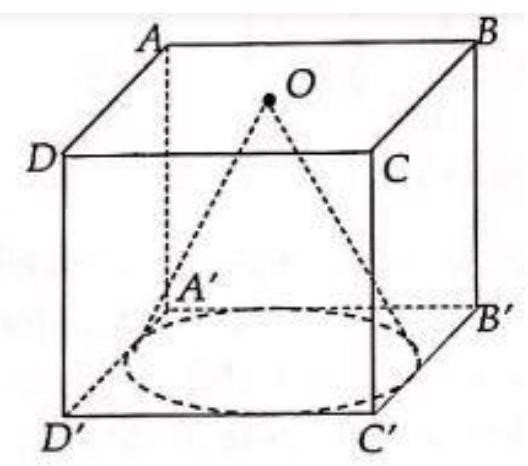
Thể tích khối lập phương là .
Ta có khối nón có đỉnh trùng với tâm một mặt của lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện có chiều cao và bán kính đáy
. Suy ra thể tích khối nón (tức là phần thể tích lượng nước tràn ra ngoài) là
.
Vậy tỉ số thể tích của lượng nước trào ra ngoài và lượng nước ban đầu của khối lập phương là .
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng ![]() . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng ![]() . Khoảng cách giữa AB và trục của hình trụ bằng:
. Khoảng cách giữa AB và trục của hình trụ bằng:
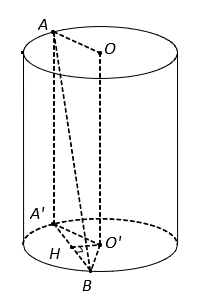
Từ hình vẽ kết hợp với giả thiết, ta có .
Gọi AA’ là đường sinh của hình trụ thì và
.
Vì nên
Gọi H là trung điểm A’B, suy ra
nên .
Tam giác ABA’ vuông tại A’ nên
Suy ra tam giác A’BO đều có cạnh bằng R nên
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính bằng chiều cao và bằng a. Trên đường tròn tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B sao cho AB = 2a. Thể tích của khối tứ diện OO’AB bằng:
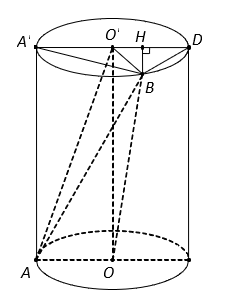
Kẻ đường sinh AA’, gọi D là điểm đối xứng với A’ qua tâm O’ và H là hình chiếu của B trên A’D.
Ta có nên
.
Trong tam giác vuông A'AB có .
Trong tam giác vuông A'BD có .
Do đó suy ra tam giác BO'D nên .
Vậy (đvtt).
Cho hình nón có đỉnh S, đường cao SO = h, đường sinh SA. Nội tiếp hình nón là một hình chóp đỉnh S, đáy là hình vuông ABCD cạnh a. Nửa góc ở đỉnh của hình nón có tan bằng:
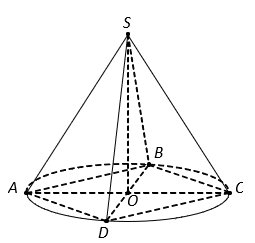
Nửa góc ở đỉnh của hình nón là góc .
Hình vuông ABCD cạnh a nên suy ra:
Trong tam giác vuông SOA, ta có .
Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là một tam giác vuông ![]() có diện tích bằng
có diện tích bằng ![]() . Góc giữa trục
. Góc giữa trục ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() . Diện tích xung quanh của hình nón đã cho bằng?
. Diện tích xung quanh của hình nón đã cho bằng?
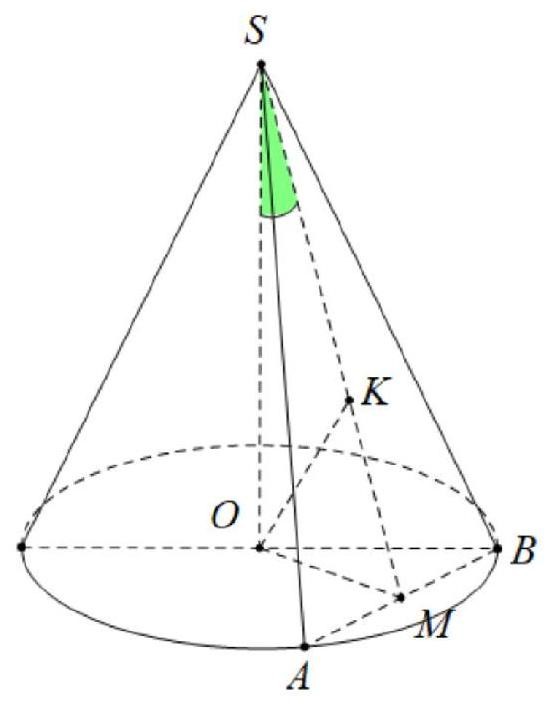
Gọi là trung điểm của
, tam giác
cân đỉnh O nên
và
suy ra
Dựng .
Theo trên có nên
.
Vậy góc tạo bởi giữa trục và mặt phẳng
là
. Tam giác vuông cân
có diện tích bằng
suy ra
.
Xét tam giác vuông có
.
Cuối cùng .
Vậy diện tích xung quanh của hình nón bằng .
Cho hình nón đỉnh S có đáy là hình tròn tâm O. Dựng hai đường sinh SA và SB, biết tam giác SAB vuông và có diện tích bằng ![]() . Góc tạo bởi giữa trục SO và mặt phẳng (SAB) bằng
. Góc tạo bởi giữa trục SO và mặt phẳng (SAB) bằng ![]() . Đường cao h của hình nón bằng:
. Đường cao h của hình nón bằng:
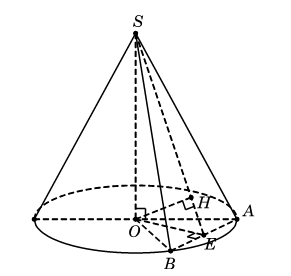
Theo giả thiết ta có tam giác SAB vuông cân tại S.
Gọi E là trung điểm AB, suy ra và
.
Ta có
.
Gọi H là hình chiếu của O trên SE, suy ra .
Ta có
Từ đó suy ra nên
Trong tam giác vuông SOE, ta có
Cho hình nón tròn xoay có chiều cao bằng 2a, bán kính đáy bằng 3a. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện bằng ![]() . Diện tích của thiết diện đó bằng?
. Diện tích của thiết diện đó bằng?
Xét hình nón đỉnh S có chiều cao , bán kính đáy
.
Thiết diện đi qua đỉnh của hình nón là tam giác SAB cân tại S.
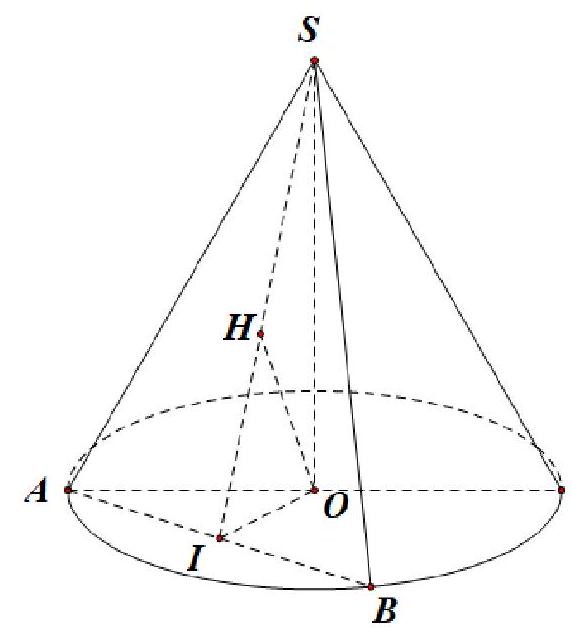
Gọi I là trung điểm của đoạn thẳng AB. Trong tam giác SOI, kẻ
Ta có:
Xét tam giác SOI vuông tại O, ta có
.
Xét tam giác AOI vuông tại I, có:
Vậy diện tích của thiết diện là:
.
Cho mặt cầu tâm O, bán kính R = a. Một hình nón có đỉnh S là ở trên mặt cầu và đáy là đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho ![]() . Độ dài đường sinh
. Độ dài đường sinh ![]() của hình nón bằng:
của hình nón bằng:
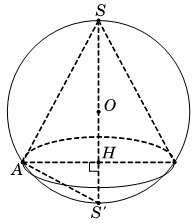
Gọi S' là điểm đối xứng của S qua tâm O và A là một điểm trên đường tròn đáy của hình nón.
Tam giác SAS’ vuông tại A và có đường cao AH nên
Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB, biết AB chắn trên đường tròn đáy một cung có số đo bằng ![]() , khoảng cách từ tâm O đến mặt phẳng (SAB) bằng
, khoảng cách từ tâm O đến mặt phẳng (SAB) bằng ![]() . Đường cao h của hình nón bằng:
. Đường cao h của hình nón bằng:
Theo giả thiết ta có tam giác OAB đều cạnh R.
Gọi E là trung điểm AB, suy ra và
.
Gọi H là hình chiếu của O trên SE, suy ra .
Ta có
Từ đó suy ra nên
Trong tam giác vuông SOE, ta có
Thiết diện qua trục hình nón là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích toàn phần và thể tích hình nón có giá trị lần lượt là:

Gọi S, O là đỉnh và tâm đường tròn đáy của hình nón,
Khi đó, ta có thiết diện qua đỉnh là tam giác SAB.
Theo đề bài, ta có tam giác SAB vuông cân tại S nên ,
Suy ra ,
và
Diện tích toàn phần của hình nón: (đvdt).
Thể tích khối nón là: (đvtt).
Cho khối trụ có hai đáy là ![]() và
và ![]() .
. ![]() lần lượt là hai đường kính của
lần lượt là hai đường kính của ![]() và
và ![]() , góc giữa
, góc giữa ![]() và
và ![]() bằng
bằng ![]() . Thể tích khối tứ diện ABCD bằng 30 . Thể tích khối trụ đã cho bằng?
. Thể tích khối tứ diện ABCD bằng 30 . Thể tích khối trụ đã cho bằng?
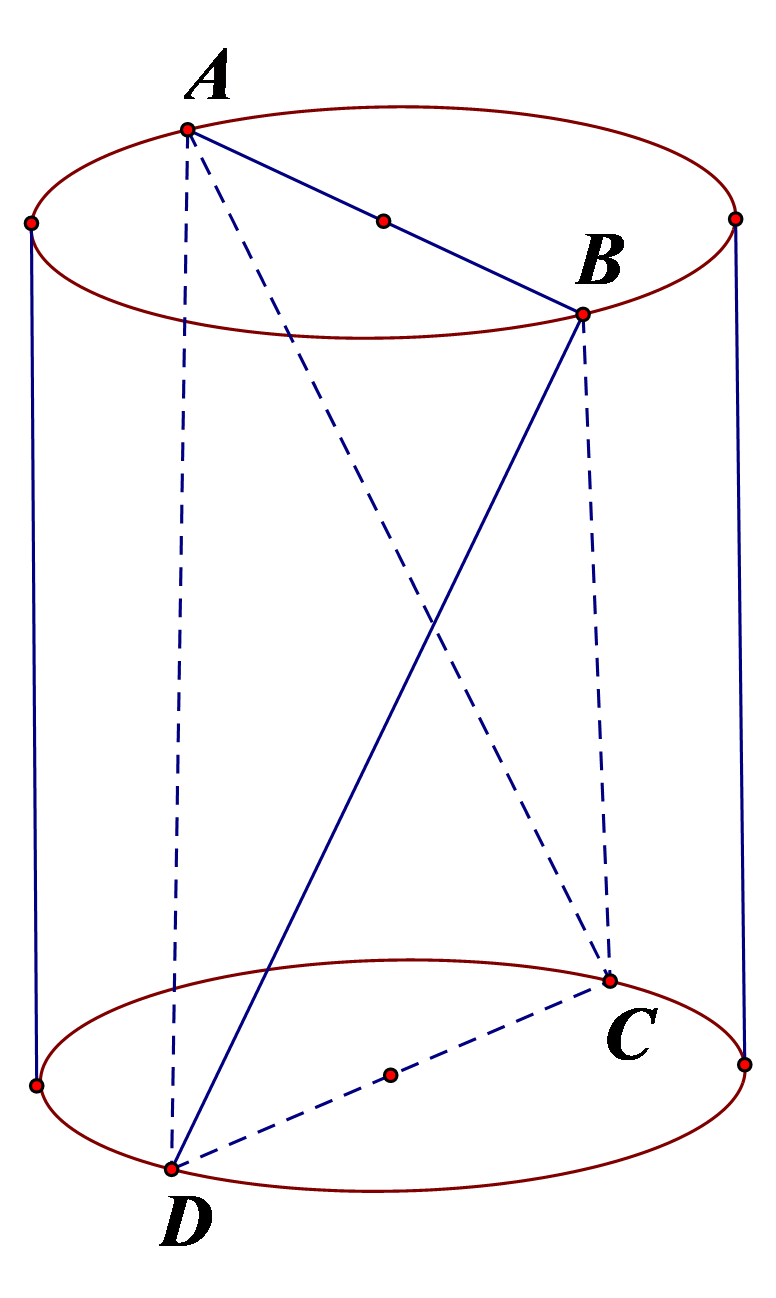
Ta chứng minh: .
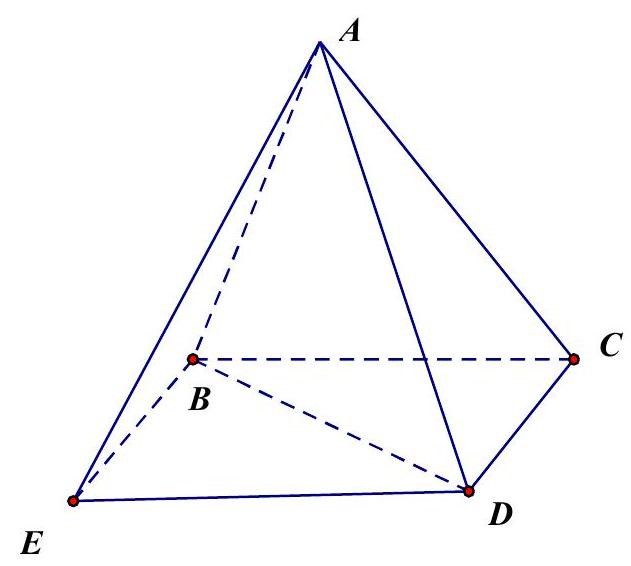
Lấy điểm E sao cho tứ giác BCDE là hình bình hành.
Khi đó .
Mà góc giữa và
bằng
nên ta có:
Ta có
Suy ra
Vậy
Chiều cao của lăng trụ bằng
Áp dụng CT thể tích lăng trụ là:
Một hình nón có đường cao bằng 9 cm nội tiếp trong một hình cầu bán kính bằng 5 cm. Tỉ số giữa thể tích khối nón và khối cầu là:
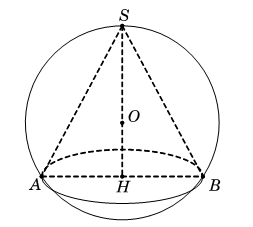
Hình vẽ kết hợp với giả thiết, ta có
Suy ra và
Thể tích khối nón (đvtt).
Thể tích khối cầu (đvtt).
Suy ra
