Cho hình vẽ:
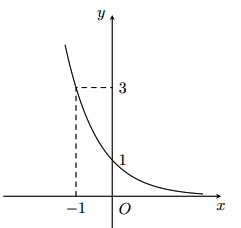
Đồ thị hình bên là của hàm số nào?
Đồ thị hàm số đi xuống nên hàm số đã cho nghịch biến nên loại hhai hàm số
Đồ thị hàm số đi qua điểm nên hàm số
thảo mãn
Cho hình vẽ:
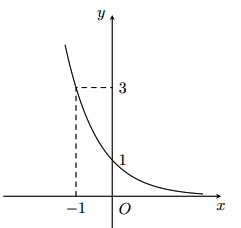
Đồ thị hình bên là của hàm số nào?
Đồ thị hàm số đi xuống nên hàm số đã cho nghịch biến nên loại hhai hàm số
Đồ thị hàm số đi qua điểm nên hàm số
thảo mãn
Cho ![]() , biết rằng biểu thức
, biết rằng biểu thức ![]() đạt giá trị nhỏ nhất bằng
đạt giá trị nhỏ nhất bằng ![]() khi
khi ![]() . Tính giá trị của
. Tính giá trị của ![]() .
.
Do nên
Ta có:
Dấu “=” xảy ra khi và chỉ khi
Vậy H đạt giá trị nhỏ nhất là 10 khi
Tìm tất cả các giá trị của tham số m để phương trình ![]() có hai nghiệm trái dấu?
có hai nghiệm trái dấu?
Đặt thì phương trình trở thành
Phương trình ban đầu có hai nghiệm trái dấu tương đương với (*) có hai nghiệm
Đặt khi đó:
Bác Thu có 600 triệu đồng mang đi gửi tiết kiện ở hai loại kì hạn khác nhau đều theo thể thức lãi kép. Bác gửi 300 triệu đồng theo kì hạn quý với lãi suất 2,1% một quý, 300 triệu đồng còn lại bác gửi theo kì hạn tháng với lãi suất 0,73%/tháng. Sau khi gửi được đúng một năm, bác rút ra một nửa số tiền ở loại kì hạn quý và gửi vào loại kì hạn theo tháng. Hỏi sau đúng hai năm kể từ khi gửi tiền lần đầu, bác Thu thu về tất cả bao nhiêu tiền lãi (làm tròn đến chữ số hàng nghìn)?
Số tiền bác Thu thu được ở năm thứ nhất là:
+ Gửi kì hạn theo quý: (triệu đồng)
+ Gửi kì hạn theo tháng: (triệu đồng)
Số tiền bác Thu thu được ở sau năm thứ hai là:
+ Gửi kì hạn theo quý: (triệu đồng)
+ Gửi kì hạn theo tháng: (triệu đồng)
Số tiền lãi bác Thu thu được là
(triệu đồng)
Có tất cả bao nhiêu cách phân tích số ![]() thành tích của ba số nguyên dương, biết rằng các cách phân tích mà các nhân tử chỉ khác nhau về thứ tự thì chỉ được tính một lần?
thành tích của ba số nguyên dương, biết rằng các cách phân tích mà các nhân tử chỉ khác nhau về thứ tự thì chỉ được tính một lần?
Ta có:
Đặt suy ra ta có hệ
Xét ba trường hợp:
Trường hợp 1: Các số bằng nhau
=> chỉ có 1 cách chọn
Trường hợp 2: Trong ba số có hai số bằng nhau, giả sử
=>
=> Có 5 cách chọn và 5 cách chọn
Trường hợp 3: Số cách chọn ba số phân biệt:
Số cách chọn là
=> Số cách chọn ba số phân biệt là
Vậy số cách phân tích thành tích ba số nguyên dương là
Cho ![]() là các số thực và hàm số
là các số thực và hàm số ![]() . Biết
. Biết ![]() . Giá trị của biểu thức
. Giá trị của biểu thức ![]() là bao nhiêu?
là bao nhiêu?
Xét hàm số
Do nên hàm số
có tập xác định
Với
Ta lại có
Vậy hàm số là hàm số lẻ
Ta có:
Xét các số thực dương ![]() thỏa mãn
thỏa mãn ![]() . Tìm giá trị nhỏ nhất
. Tìm giá trị nhỏ nhất ![]() của biểu thức
của biểu thức ![]()
Theo bài ta có:
Mà
=> . Khi đó ta có:
Xét hàm số ta có:
Ta có bảng biến thiên như sau:
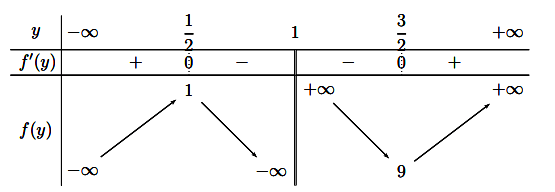
Từ bảng biến thiên ta thấy
Theo dự định số lượng thức ăn dự trữ của nông trại B sẽ hết sau 100 ngày, nhưng thực tế mức tiêu thụ của vật nuôi tăng thêm 4% mỗi ngày (ngày sau tăng 4% so với ngày trước đó). Hỏi lượng thức ăn dữ trữ thực tế sẽ hết sau khoảng bao nhiêu ngày? (làm tròn đến hàng đơn vị)
Theo dự định, mỗi ngày lượng thức ăn tiêu thụ là: (lượng thức ăn)
Lượng thức ăn mà vật nuôi ăn hết ở ngày thứ k là: (lượng thức ăn)
Xác định số tự nhiên n nhỏ nhất để:
Cho các hàm số ![]() có đồ thị như hình vẽ. Đường thẳng
có đồ thị như hình vẽ. Đường thẳng ![]() cắt trục hoành, đồ thị hàm số
cắt trục hoành, đồ thị hàm số ![]() và
và ![]() lần lượt tại
lần lượt tại ![]() . Biết rằng
. Biết rằng ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
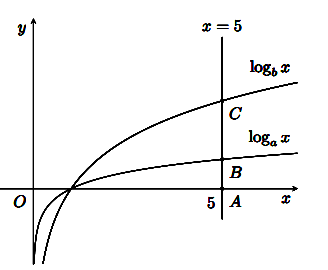
Ta có:
Theo bài ra ta có:
Tìm tập xác định của hàm số ![]()
Điều kiện xác định
=> Tập xác định của hàm số là
Mệnh đề nào sau đây là mệnh đề sai?
Ta thấy:
Do vậy đồ thị của hàm số không có tiệm cận đứng
Tìm đạo hàm của hàm số ![]()
Ta có:
Tìm điều kiện của x để hàm số ![]() có nghĩa?
có nghĩa?
Ta có điều kiện xác định
Một người gửi vào ngân hàng 200 triệu đồng vào tài khoản tiết kiệm ngân hàng với lãi suất 0,6%/ tháng, cứ sau mỗi tháng người đó rút ra 500 nghìn đồng. Hỏi sau đúng 36 lần rút tiền thì số tiền còn lại trong tài khoản của người đó gần nhất với phương án nào sau đây? (Biết rằng lãi suất không thay đổi và tiền lại mỗi tháng tính theo số tiền thực tế trong tài khoản của tháng đó?
Số tiền còn lại trong tài khoản sau tháng thứ 1 là: (triệu đồng)
Số tiền còn lại trong tài khoản sau tháng thứ 2 là:
(triệu đồng)
Số tiền còn lại trong tài khoản sau tháng thứ 3 là:
(triệu đồng)
Cứ tiếp tục quá trình thì số tiền còn lại trong tài khoản sau tháng thứ 36 là:
(triệu đồng)
Cho hai số thực dương x và y thỏa mãn ![]() . Tính giá trị nhỏ nhất của
. Tính giá trị nhỏ nhất của ![]()
Ta có:
Nếu
Nếu thì
Xét hàm số ta có:
Lập bảng biến thiên ta suy ra được
Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực?
Ta có:
là các hàm số không xác định trên
Vì nghịch biến trên
Tập xác định của hàm số ![]() là:
là:
Hàm số xác định nếu
Vậy tập xác định
Đẳng thức nào sau đây đúng với mọi số dương ![]() ?
?
Ta có:
Hàm số nào sau đây phù hợp với hình vẽ:
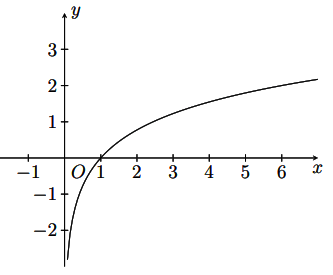
Ta có: và hàm số đồng biến trên
nên chỉ có hàm số
thỏa mãn
Cho các mệnh đề sau:
(i) Cơ số của logarit phải là số dương.
(ii) Chỉ số thực dương mới có logarit.
(iii) ![]() với mọi
với mọi ![]() .
.
(iv) ![]() với mọi
với mọi ![]() .
.
Số mệnh đề đúng là:
(i) Sai vì cơ số của chỉ cần thỏa mãn
(ii) Đúng vì điều kiện có nghĩa của là
(iii) Sai vì với mọi
(iv) Sai vì nếu thì các biểu thức
không có nghĩa.
