Lớp 12 Toán 12

Đề Ôn tập chương 2 (Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 30 câu
  • Điểm số bài kiểm tra: 30 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng cao
    Tìm giá trị thực của tham số m để hàm số đồng biến trên khoảng

    Biết rằng tập tất cả các giá trị thực của tham số m để hàm số y = \frac{1}{3}{x^3} - \left( {m - 1} ight){x^2} - \left( {m - 3} ight) + 2017m đồng biến trên khoảng \left( { - 3; - 1} ight) và \left( {0;3} ight) là đoạn T = \left[ {a;b} ight]. Tính {a^2} + {b^2}

    Hướng dẫn:

     Tập xác định D = \mathbb{R}

    y' = {x^2} - 2\left( {m - 1} ight)x - \left( {m - 3} ight)

    Hàm số đã cho đồng biến trên \left( {0;3} ight) tức là

    \Leftrightarrow \frac{{{x^2} + 2x + 3}}{{2x + 1}} \geqslant m;\forall x \in \left( {0;3} ight)

    Xét f\left( x ight) = \frac{{{x^2} + 2x + 3}}{{2x + 1}};\forall x \in \left( {0;3} ight)

    Ta có:

    \begin{matrix} f'\left( x ight) = \dfrac{{2{x^2} + 2x - 4}}{{{{\left( {2x + 1} ight)}^2}}} \hfill \\ \Rightarrow f'\left( x ight) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1} \\ {x = - 2\left( L ight)} \end{array}} ight. \hfill \\ \end{matrix}

    Ta có bảng biến thiên

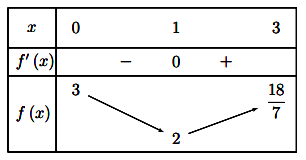
    Tìm giá trị thực của tham số m để hàm số đồng biến trên khoảng

    Từ bảng biến thiên suy ra f\left( x ight) \geqslant m;\forall x \in \left( {0;3} ight) \Rightarrow m \leqslant 2

    Hàm số đã cho đồng biến trên \left( { - 3; - 1} ight) tức là y' \leqslant 0;\forall x \in \left( { - 3;1} ight)

    \Leftrightarrow \frac{{{x^2} + 2x + 3}}{{2x + 1}} \geqslant m;\forall x \in \left( { - 3;1} ight)

    Xét f\left( x ight) = \frac{{{x^2} + 2x + 3}}{{2x + 1}};\forall x \in \left( { - 3;1} ight) ta có:

    f'\left( x ight) = \frac{{2{x^2} + 2x - 4}}{{{{\left( {2x + 1} ight)}^2}}} \Rightarrow f'\left( x ight) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1\left( L ight)} \\ {x = - 2} \end{array}} ight.

    Ta có bảng biến thiên như sau:

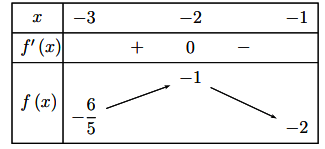
    Tìm giá trị thực của tham số m để hàm số đồng biến trên khoảng

    Từ bảng biến thiên suy ra f\left( x ight) \leqslant m \Leftrightarrow m \geqslant 1

    Kết hợp kết quả ta được - 1 \leqslant m \leqslant 2 \Rightarrow a = - 1;b = 2

  • Câu 2: Nhận biết
    Tập xác định của hàm số

    Tập xác định của hàm số y = \log {\left( {x - 2} ight)^2} là:

    Hướng dẫn:

    Hàm số y = \log {\left( {x - 2} ight)^2} xác định nếu {\left( {x - 2} ight)^2} > 0 \Leftrightarrow x e 2

    Vậy tập xác định D = \mathbb{R}\backslash \left\{ 2 ight\}

  • Câu 3: Vận dụng
    Tính giá trị biểu thức K

    Tính giá trị biểu thức: K = \log \left( {\tan {1^0}} ight) + \log \left( {\tan {2^0}} ight) + \log \left( {\tan {3^0}} ight) + ... + \log \left( {\tan {{89}^0}} ight)

    Hướng dẫn:

    Ta có:

    \begin{matrix} K = \log \left( {\tan {1^0}} ight) + \log \left( {\tan {2^0}} ight) + \log \left( {\tan {3^0}} ight) + ... + \log \left( {\tan {{89}^0}} ight) \hfill \\ K = \log \left( {\tan {1^0}.\tan {2^0}.\tan {3^0}....\tan {{89}^0}} ight) \hfill \\ K = \log \left[ {\tan {1^0}.\tan {2^0}.\tan {3^0}....\tan \left( {{{90}^0} - {2^0}} ight).\tan \left( {{{90}^0} - {1^0}} ight)} ight] \hfill \\ K = \log \left[ {\tan {1^0}.\tan {2^0}.\tan {3^0}....\cot {2^0}.\cot {1^0}} ight] \hfill \\ K = \log \left[ {\left( {\tan {1^0}.\cot {1^0}} ight).\left( {\tan {2^0}.\cot {2^0}} ight)...} ight] = \log 1 = 0 \hfill \\ \end{matrix}

  • Câu 4: Nhận biết
    Tìm đạo hàm của hàm số

    Tìm đạo hàm của hàm số y = \ln \left( {1 + {e^{2x}}} ight)

    Hướng dẫn:

    Ta có: y' = \left( {\ln \left( {1 + {e^{2x}}} ight)} ight)' = \frac{{\left( {1 + {e^{2x}}} ight)'}}{{1 + {e^{2x}}}} = \frac{{2{e^{2x}}}}{{{{\left( {{e^{2x}} + 1} ight)}^2}}}

  • Câu 5: Vận dụng cao
    Tình thời gian tiêu thụ hết thức ăn dự trữ

    Theo dự định số lượng thức ăn dự trữ của nông trại B sẽ hết sau 100 ngày, nhưng thực tế mức tiêu thụ của vật nuôi tăng thêm 4% mỗi ngày (ngày sau tăng 4% so với ngày trước đó). Hỏi lượng thức ăn dữ trữ thực tế sẽ hết sau khoảng bao nhiêu ngày? (làm tròn đến hàng đơn vị)

    Hướng dẫn:

    Theo dự định, mỗi ngày lượng thức ăn tiêu thụ là:  (lượng thức ăn)

    Lượng thức ăn mà vật nuôi ăn hết ở ngày thứ k là: \frac{1}{{100}}{\left( {1 + 4\% } ight)^{k - 1}};\left( {k \in {\mathbb{N}^*}} ight) (lượng thức ăn)

    Xác định số tự nhiên n nhỏ nhất để:

    \begin{matrix} \dfrac{1}{{100}} + \dfrac{1}{{100}}{\left( {1 + 4\% } ight)^1} + \dfrac{1}{{100}}{\left( {1 + 4\% } ight)^2} + ... + \dfrac{1}{{100}}{\left( {1 + 4\% } ight)^{n - 1}} \geqslant 1 \hfill \\ \Leftrightarrow \dfrac{1}{{100}} + \dfrac{1}{{100}}1,04 + \dfrac{1}{{100}}.1,{04^2} + ... + \dfrac{1}{{100}}.1,{04^{n - 1}} \geqslant 1 \hfill \\ \Leftrightarrow \dfrac{1}{{100}}.\left( {1,04 + 1,{{04}^2} + ... + 1,{{04}^{n - 1}}} ight) \geqslant 1 \hfill \\ \Leftrightarrow \dfrac{1}{{100}}.\left( {\dfrac{{1,{{04}^{n - 1}} - 1}}{{1,04 - 1}}} ight) \geqslant 1 \hfill \\ \Leftrightarrow 1,{04^{n - 1}} - 1 \geqslant 4 \hfill \\ \Leftrightarrow n - 1 \geqslant {\log _{1,04}}5 \hfill \\ \Leftrightarrow n \geqslant {\log _{1,04}}5 + 1 \hfill \\ \Leftrightarrow n \geqslant 42,03 \to {n_{\min }} = 43 \hfill \\ \end{matrix}

  • Câu 6: Vận dụng cao
    Tổng 2 nghiệm PT mũ

    Gọi x_1, x_2 là hai nghiệm của phương trình {2^{{x^2} + 4}} = {2^{2\left( {{x^2} + 1} ight)}} + \sqrt {{2^{2\left( {{x^2} + 2} ight)}} - {2^{{x^2} + 3}} + 1}.  Khi đó, tổng hai nghiệm bằng?

    Hướng dẫn:

     Ta có: {2^{{x^2} + 4}} = {2^{2\left( {{x^2} + 1} ight)}} + \sqrt {{2^{2\left( {{x^2} + 2} ight)}} - {2^{{x^2} + 3}} + 1}

    \Leftrightarrow {8.2^{{x^2} + 1}} = {2^{2\left( {{x^2} + 1} ight)}} + \sqrt {{{4.2}^{2\left( {{x^2} + 1} ight)}} - {{4.2}^{{x^2} + 1}} + 1}

    Đặt t = {2^{{x^2} + 1}}\left( {t \geqslant 2} ight), phương trình trên tương đương với:

    8t = {t^2} + \sqrt {4{t^2} - 4t + 1} \Leftrightarrow {t^2} - 6t - 1 = 0 \Leftrightarrow t = 3 + \sqrt {10} (vì t \geq 2).

    Từ đó suy ra {2^{{x^2} + 1}} = 3 + \sqrt {10} \Leftrightarrow \left[ \begin{gathered} {x_1} = \sqrt {{{\log }_2}\frac{{3 + \sqrt {10} }}{2}} \hfill \\ {x_2} = - \sqrt {{{\log }_2}\frac{{3 + \sqrt {10} }}{2}} \hfill \\ \end{gathered} ight.

     

    Vậy tổng hai nghiệm bằng 0.

  • Câu 7: Vận dụng
    Có tất cả bao nhiêu cách phân tích số

    Có tất cả bao nhiêu cách phân tích số {15^9} thành tích của ba số nguyên dương, biết rằng các cách phân tích mà các nhân tử chỉ khác nhau về thứ tự thì chỉ được tính một lần?

    Hướng dẫn:

    Ta có:

    \begin{matrix} {15^9} = {3^9}{.5^9} \hfill \\ \Rightarrow {15^9} = \underbrace {3...3}_9.\underbrace {5...5}_9 \hfill \\ \Rightarrow {15^9} = \underbrace {\underbrace {3...3}_{{a_1}}.\underbrace {5...5}_{{b_1}}}_x.\underbrace {\underbrace {3...3}_{{a_2}}.\underbrace {5...5}_{{b_2}}}_y.\underbrace {\underbrace {3...3}_{{a_3}}.\underbrace {5...5}_{{b_3}}}_z \hfill \\ \end{matrix}

    Đặt \left\{ {\begin{array}{*{20}{c}} {x = {3^{{a_1}}}{5^{{b_1}}}} \\ {y = {3^{{a_2}}}{5^{{b_2}}}} \\ {z = {3^{{z_1}}}{5^{{z_2}}}} \end{array}} ight. suy ra ta có hệ \left\{ {\begin{array}{*{20}{c}} {{a_1} + {a_2} + {a_3} = 9} \\ {{b_1} + {b_2} + {b_3} = 9} \end{array}} ight.

    Xét ba trường hợp:

    Trường hợp 1: Các số x,y,z bằng nhau

    => chỉ có 1 cách chọn

    Trường hợp 2: Trong ba số x,y,z có hai số bằng nhau, giả sử x = y

    =>\left\{ {\begin{array}{*{20}{c}} {{a_1} = {a_2}} \\ {{b_1} = {b_2}} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {2{a_1} + {a_3} = 9} \\ {2{b_a} + {b_3} = 9} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{a_3} = 9 - 2{a_1}} \\ {{b_3} = 9 - 2{a_1}} \end{array}} ight.

    => Có 5 cách chọn {a_1} và 5 cách chọn {b_1}

    Trường hợp 3: Số cách chọn ba số phân biệt:

    Số cách chọn \left\{ {\begin{array}{*{20}{c}} {{a_1} + {a_2} + {a_3} = 9} \\ {{b_1} + {b_2} + {b_3} = 9} \end{array}} ight. là C_{11}^2.C_{11}^2

    => Số cách chọn ba số phân biệt là C_{11}^2.C_{11}^2 - 24.3 - 1

    Vậy số cách phân tích {15^9} thành tích ba số nguyên dương là \frac{{C_{11}^2.C_{11}^2 - 24.3 - 1}}{{3!}} + 25 = 517

  • Câu 8: Vận dụng
    Khẳng định nào sau đây là đúng?

    Cho biểu thức P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.{{\left( {{a^2}{b^2}} ight)}^{\frac{2}{3}}}} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6} với a và b là các số thực dương. Khẳng định nào sau đây là đúng?

    Hướng dẫn:

     Thực hiện thu gọn biểu thức như sau:

    \begin{matrix} P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.{{\left( {{a^2}{b^2}} ight)}^{\frac{2}{3}}}} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.\left( {{a^{\frac{4}{3}}}{b^{\frac{4}{3}}}} ight)} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{5}{6}}}.b} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {\left\{ {{a^{\frac{1}{3}}}.{a^{\frac{{ - 5}}{{12}}}}.{b^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {\left\{ {{a^{\frac{{ - 1}}{{12}}}}.{b^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {a^{\frac{{ - 1}}{2}}}.{b^{ - 3}} = \dfrac{1}{{{b^3}\sqrt a }} = \dfrac{{\sqrt a }}{{a{b^3}}} \hfill \\ \end{matrix}

  • Câu 9: Thông hiểu
    Mệnh đề nào sau đây là mệnh đề sai?

    Mệnh đề nào sau đây là mệnh đề sai?

    Hướng dẫn:

    Ta thấy: y = {2^{ - x}} = {\left( {\frac{1}{2}} ight)^x}

    Do vậy đồ thị của hàm số y = {2^{ - x}} không có tiệm cận đứng

  • Câu 10: Thông hiểu
    Tính giá trị biểu thức A

    Cho {5^x} = 2. Tính A = {25^x} + {5^{2 - x}}

    Hướng dẫn:

    Ta có: A = {25^x} + {5^{2 - x}} = {\left( {{5^x}} ight)^2} + \frac{{25}}{{{5^x}}} = \frac{{33}}{2}

  • Câu 11: Thông hiểu
    Tính giá trị biểu thức T

    Cho a,b > 0, viết {a^{\frac{2}{3}}}.\sqrt a về dạng {a^x} và \sqrt[3]{{b\sqrt {b\sqrt b } }} về dạng {b^y}. Tình giá trị biểu thức T = 6a + 12y

    Hướng dẫn:

    Ta có:

    \begin{matrix} {a^{\frac{2}{3}}}.\sqrt a = {a^{\frac{2}{3}}}.{a^{\frac{1}{2}}} = {a^{\frac{2}{3} + \frac{1}{2}}} = {a^{\frac{7}{6}}} \hfill \\ \Rightarrow {a^x} = {a^{\frac{7}{6}}} \hfill \\ \Rightarrow x = \dfrac{7}{6} \hfill \\ \sqrt[3]{{b\sqrt {b\sqrt b } }} = {\left( {b\sqrt {{b^{\frac{3}{2}}}} } ight)^{\frac{1}{3}}} = {\left( {b.{b^{\frac{3}{4}}}} ight)^{\frac{1}{3}}} = {\left( {{b^{\frac{7}{4}}}} ight)^{\frac{1}{3}}} = {b^{\frac{7}{{12}}}} \hfill \\ \Rightarrow {b^y} = {b^{\frac{7}{{12}}}} \Rightarrow y = \dfrac{7}{{12}} \hfill \\ \Rightarrow T = 14 \hfill \\ \end{matrix}

  • Câu 12: Vận dụng cao
    Tìm chữ số đầu tiên

    Biết số nguyên dương M sẽ có chữ số đầu tiên là k (khi biểu diễn thập phân) nếu \log k \leqslant \left\{ {\log M} ight\} < \log \left( {k + 1} ight) trong đó kí hiệu \left\{ a ight\} chỉ phần lẻ của số thập phân a (ví dụ \left\{ {300,2} ight\} = 0,2). Hỏi số M = {2^{400}} có chữ số đầu tiên là bao nhiêu?

    Hướng dẫn:

    Ta có: \begin{matrix} \left\{ {\log M} ight\} \approx 0,41 \hfill \\ \log 2 < \left\{ {\log M} ight\} < \log 3 \hfill \\ \end{matrix} nên chữ số đầu tiên của M là 2

  • Câu 13: Thông hiểu
    Biến đổi biểu thức P

    Viết biểu thức P = \sqrt {{x^5}} .\sqrt[3]{{{x^2}}}.\sqrt[5]{{{x^3}}};\left( {x > 0} ight) dưới dạng lũy thừa với số mũ hữu tỉ

    Hướng dẫn:

    Ta có: P = \sqrt {{x^5}} .\sqrt[3]{{{x^2}}}.\sqrt[5]{{{x^3}}} = {x^{\frac{1}{5}}}.{x^{\frac{2}{3}}}.{x^{\frac{3}{5}}} = {x^{\frac{{113}}{{30}}}}

  • Câu 14: Thông hiểu
    Tính đạo hàm của hàm số lũy thừa

    Tính đạo hàm của hàm số y = \left( {{x^2} + 2x - 2} ight){.5^x}

    Hướng dẫn:

     Ta có:

    \begin{matrix} y' = \left( {{x^2} + 2x - 2} ight)'{.5^x} + \left( {{5^x}} ight)'.\left( {{x^2} + 2x - 2} ight) \hfill \\ \Rightarrow y' = \left( {2x + 2} ight){.5^x} + \left( {{x^2} + 2x - 2} ight){.5^x}.\ln 5 \hfill \\ \end{matrix}

  • Câu 15: Vận dụng cao
    Tính tổng S

    Cho biểu thức f\left( x ight) = \frac{1}{{{{2018}^x} + \sqrt {2018} }}. Tính tổng S = \sqrt {2018} \left[ {f\left( { - 2017} ight) + f\left( { - 2016} ight) + ... + f\left( 0 ight) + f\left( 1 ight) + f\left( {2018} ight)} ight]

    Hướng dẫn:

     Trước hết ta chứng minh với a + b = 1 \Rightarrow f\left( a ight) + f\left( b ight) = \frac{1}{{\sqrt {2018} }}

    Thật vậy

    \begin{matrix} f\left( a ight) + f\left( b ight) = \dfrac{1}{{{{2018}^a} + \sqrt {2018} }} + \dfrac{1}{{{{2018}^b} + \sqrt {2018} }} \hfill \\ \Rightarrow f\left( a ight) + f\left( b ight) = \dfrac{1}{{\sqrt {2018} }}\left( {\dfrac{1}{{{{2018}^{a - \dfrac{1}{2}}} + 1}} + \dfrac{1}{{{{2018}^{b - \dfrac{1}{2}}} + 1}}} ight) \hfill \\ \Rightarrow f\left( a ight) + f\left( b ight) = \dfrac{1}{{\sqrt {2018} }}\left( {\dfrac{1}{{{{2018}^{a - \dfrac{1}{2}}} + 1}} + \dfrac{1}{{{{2018}^{1 - a - \dfrac{1}{2}}} + 1}}} ight) \hfill \\ \Rightarrow f\left( a ight) + f\left( b ight) = \dfrac{1}{{\sqrt {2018} }}\left( {\dfrac{1}{{{{2018}^{a - \dfrac{1}{2}}} + 1}} + \dfrac{{{{2018}^{a - \dfrac{1}{2}}}}}{{{{2018}^{a - \dfrac{1}{2}}} + 1}}} ight) \hfill \\ \Rightarrow f\left( a ight) + f\left( b ight) = \dfrac{1}{{\sqrt {2018} }} \hfill \\ \end{matrix}

    Theo tính chất trên ta có:

    \begin{matrix} f\left( { - 2017} ight) + f\left( {2018} ight) = \dfrac{1}{{\sqrt {2018} }} \hfill \\ f\left( { - 2016} ight) + f\left( {2017} ight) = \dfrac{1}{{\sqrt {2018} }} \hfill \\ .... \hfill \\ f\left( 0 ight) + f\left( 1 ight) = \dfrac{1}{{\sqrt {2018} }} \hfill \\ \Rightarrow S = 2018 \hfill \\ \end{matrix}

  • Câu 16: Vận dụng cao
    Tìm tất cả các giá trị thực của tham số a

    Tìm tất cả các giá trị thực của tham số a > 0 thỏa mãn {\left( {{2^a} + \frac{1}{{{2^a}}}} ight)^{2017}} \leqslant {\left( {{2^{2017}} + \frac{1}{{{2^{2017}}}}} ight)^a}

    Hướng dẫn:

     Xét hàm số f\left( x ight) = \frac{{\ln \left( {{2^x} + {2^{ - x}}} ight)}}{x} \Rightarrow f'\left( x ight) = \frac{{\left( {{2^x} - {2^{ - x}}} ight)\ln {2^x} - \left( {{2^x} + {2^{ - x}}} ight)\ln \left( {{2^x} + {2^{ - x}}} ight)}}{{{x^2}\left( {{2^x} + {2^{ - x}}} ight)}}

    Vì \left\{ {\begin{array}{*{20}{c}} {\ln {2^x} > \ln \left( {{2^x} + {2^{ - x}}} ight)} \\ {0 < {2^x} - {2^{ - x}} < {2^x} + {2^{ - x}}} \end{array}} ight. \Rightarrow f'\left( x ight) < 0

    Vậy hàm số nghịch biến

    Do đó:

    \begin{matrix} {\left( {{2^a} + \dfrac{1}{{{2^a}}}} ight)^{2017}} \leqslant {\left( {{2^{2017}} + \dfrac{1}{{{2^{2017}}}}} ight)^a} \hfill \\ \Leftrightarrow 2017\ln \left( {{2^a} + {2^{ - a}}} ight) \leqslant a\ln \left( {{2^{2017}} + {2^{ - 2017}}} ight) \hfill \\ \Leftrightarrow \dfrac{{\ln \left( {{2^a} + {2^{ - a}}} ight)}}{a} \leqslant \dfrac{{\ln \left( {{2^{2017}} + {2^{ - 2017}}} ight)}}{{2017}} \Leftrightarrow a \geqslant 2017 \hfill \\ \end{matrix}

     

  • Câu 17: Vận dụng
    Chọn khẳng định nào đúng?

    Cho a{\log _6}3 + b{\log _6}2 + c{\log _6}5 = 5 với a,b,c là các số tự nhiên. Trong các khẳng định sau, khẳng định nào đúng?

    Hướng dẫn:

    Ta có:

    \begin{matrix} a{\log _6}3 + b{\log _6}2 + c{\log _6}5 = 5 \hfill \\ \Leftrightarrow {3^a}{.2^b}{.5^c} = 5 \hfill \\ \end{matrix}

    Do a,b,c \in \mathbb{N} nên chỉ có một bộ số \left( {a,b,c} ight) = \left( {0,0,1} ight) thỏa mãn

  • Câu 18: Thông hiểu
    Xác định giá trị của biểu thức logarit

    Với các số a, b > 0 thỏa mãn {a^2} + {b^2} = 6ab, biểu thức {\log _2}\left( {a + b} ight) bằng:

    Hướng dẫn:

    Ta có: 

    \begin{matrix} {a^2} + {b^2} = 6ab \hfill \\ \Rightarrow {\left( {a + b} ight)^2} = 8ab \hfill \\ \Rightarrow {\log _2}{\left( {a + b} ight)^2} = {\log _2}\left( {8ab} ight) \hfill \\ \Rightarrow 2{\log _2}\left( {a + b} ight) = {\log _2}8 + {\log _2}a + {\log _2}b \hfill \\ \Rightarrow {\log _2}\left( {a + b} ight) = \dfrac{1}{2}\left( {{{\log }_2}8 + {{\log }_2}a + {{\log }_2}b} ight) \hfill \\ \Rightarrow {\log _2}\left( {a + b} ight) = \dfrac{1}{2}\left( {3 + {{\log }_2}a + {{\log }_2}b} ight) \hfill \\ \end{matrix}

  • Câu 19: Vận dụng cao
    Tìm tất cả các giá trị thực của tham số

    Tìm tất cả các giá trị thực của tham số m để bất phương trình {\log _2}\left( {7{x^2} + 7} ight) \geqslant {\log _2}\left( {m{x^2} + 4x + m} ight),{\text{ }}\forall x \in \mathbb{R} \, \, (1)

    Hướng dẫn:

     Bất phương trình tương đương 7{x^2} + 7 \geqslant m{x^2} + 4x + m > 0,{\text{ }}\forall x \in \mathbb{R}

    \Leftrightarrow \left\{ \begin{gathered} \left( {7 - m} ight){x^2} - 4x + 7 - m \geqslant 0{\text{ }}(2) \hfill \\ m{x^2} + 4x + m > 0{\text{ }}(3) \hfill \\ \end{gathered} ight.,{\text{ }}\forall x \in \mathbb{R}.

    m=7: (2) không thỏa \forall x \in \mathbb{R}

    m=0: (3) không thỏa \forall x \in \mathbb{R}

    (1) thỏa mãn \forall x \in \mathbb{R}  \Leftrightarrow \left\{ \begin{gathered} 7 - m > 0 \hfill \\ {{\Delta '}_2} = 4 - {\left( {7 - m} ight)^2} \leqslant 0 \hfill \\ m > 0 \hfill \\ {{\Delta '}_3} = 4 - {m^2} < 0 \hfill \\ \end{gathered} ight.{\text{ }}

    \Leftrightarrow {\text{ }}\left\{ \begin{gathered} m < 7 \hfill \\ m \leqslant 5 \hfill \\ m > 0 \hfill \\ m > 2 \hfill \\ \end{gathered} ight.{\text{ }} \Leftrightarrow {\text{ }}2 < m \leqslant 5.

    Vậy m \in \left( {2;5} ight].

  • Câu 20: Nhận biết
    Hàm số nào sau đây đồng biến trên tập số thực

    Hàm số nào sau đây đồng biến trên \mathbb{R}?

    Hướng dẫn:

    Do \frac{{\sqrt 2 + \sqrt 3 }}{3} > 1 nên hàm số y = {\left( {\frac{{\sqrt 2 + \sqrt 3 }}{3}} ight)^x} đồng biến trên \mathbb{R} 

  • Câu 21: Nhận biết
    Hàm số nào nghịch biến trên tập số thực?

    Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực?

    Hướng dẫn:

     Ta có:

    y = {\log _{\frac{\pi }{4}}}\left( {2{x^2} + 1} ight);y = {\log _{\frac{1}{2}}}x là các hàm số không xác định trên \mathbb{R}

    Vì \frac{2}{e} < 1 \Rightarrow y = {\left( {\frac{2}{e}} ight)^x} nghịch biến trên \mathbb{R}

  • Câu 22: Vận dụng
    Tính số dân của tỉnh A năm 2025

    Cho biết năm 2018, tỉnh A có 2 triệu người và tỉ lệ dân số là 1,4%/năm. Hỏi đến năm 2025 tỉnh A có bao nhiêu người, nếu tỉ lệ tăng dân số hằng năm không đổi?

    Gợi ý:

    Công thức ước tính dân số S = A.{e^{n.i}}

    Trong đó A là dân số của nam lấy làm mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hằng năm.

    Hướng dẫn:

    Ta có: A = 2, n = 7; I = 0,014

    Số dân tỉnh A đến năm 2025 là S = 2.{e^{7.0,014}} \approx 2,2059 triệu người.

  • Câu 23: Thông hiểu
    Tính P = ab + 1

    Cho hai số thực dương a và b thỏa mãn {\log _9}{a^4} + {\log _3}b = 8 và {\log _3}a + {\log _{\sqrt[3]{3}}}b = 9. Giá trị của biểu thức P = ab + 1 là:

    Hướng dẫn:

    Theo điều kiện ta có:

     \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {{{\log }_9}{a^4} + {{\log }_3}b = 8} \\ {{{\log }_3}a + {{\log }_{\sqrt[3]{3}}}b = 9} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {2{{\log }_9}a + {{\log }_3}b = 8} \\ {{{\log }_3}a + 3{{\log }_3}b = 9} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{{\log }_9}a = 3} \\ {{{\log }_3}b = 2} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a = 27} \\ {b = 9} \end{array}} ight. \hfill \\ \Rightarrow P = ab + 1 = 244 \hfill \\ \end{matrix}

  • Câu 24: Nhận biết
    Tập xác định của hàm số y

    Tập xác định của hàm số y = {\left( {x + 3} ight)^{\frac{3}{2}}} - \sqrt[4]{{5 - x}} là:

    Hướng dẫn:

    Điều kiện xác định: \left\{ {\begin{array}{*{20}{c}} {x + 3 > 0} \\ {5 - x \geqslant 0} \end{array}} ight. \Rightarrow - 3 < x \leqslant 5

    => Tập xác định của hàm số là D = \left( { - 3;5} ight]

  • Câu 25: Nhận biết
    Giá trị của biểu thức

    Giá trị của biểu thức P = {\left( {1 + \sqrt 3 } ight)^{2016}}.{\left( {3 - \sqrt 3 } ight)^{2016}} bằng:

    Hướng dẫn:

    Ta có:

    P = {\left( {1 + \sqrt 3 } ight)^{2016}}.{\left( {3 - \sqrt 3 } ight)^{2016}}

    = {\left[ {\left( {1 + \sqrt 3 } ight)\left( {3 - \sqrt 3 } ight)} ight]^{2016}} = {\left( {2\sqrt 3 } ight)^{2016}} = {12^{1008}}

  • Câu 26: Thông hiểu
    Đẳng thức nào sau đây đúng với mọi số dương x?

    Đẳng thức nào sau đây đúng với mọi số dương x?

    Hướng dẫn:

    Ta có: \left( {\log x} ight)' = \frac{1}{{x\ln 10}};\forall x > 0

  • Câu 27: Vận dụng cao
    Tính giá trị nhỏ nhất của biểu thức

    Cho x,y > 0 thỏa mãn \log \left( {x + 2y} ight) = \log x + \log y. Khi đó giá trị nhỏ nhất của biểu thức M = \frac{{{x^2}}}{{1 + 2y}} + \frac{{4{y^2}}}{{1 + x}} là:

    Hướng dẫn:

    Ta có:

    \begin{matrix} \log \left( {x + 2y} ight) = \log x + \log y \hfill \\ \Rightarrow x + 2y = xy \hfill \\ \end{matrix}

    Đặt 2y = z. Ta có: x,z > 0 thỏa mãn 2\left( {x + z} ight) = xz \leqslant {\left( {\frac{{x + z}}{2}} ight)^2} \Rightarrow x + z \geqslant 8

    Ta lại có

    M = \frac{{{x^2}}}{{1 + z}} + \frac{{{z^2}}}{{1 + x}} \geqslant \frac{{{{\left( {x + z} ight)}^2}}}{{2 + x + z}} = x + z - 2 + \frac{4}{{2 + x + z}}

     

    Xét hàm số

    \begin{matrix} f\left( t ight) = t - 2 + \dfrac{4}{{2 + t}} \Rightarrow f'\left( t ight) = 1 - \dfrac{4}{{{{\left( {t + 2} ight)}^2}}} > 0;\forall t \geqslant 8 \hfill \\ \Rightarrow \mathop {\min f\left( t ight)}\limits_{t \geqslant 8} = f\left( 8 ight) = \dfrac{{32}}{5} \hfill \\ \end{matrix}

    Vậy giá trị nhỏ nhất của biểu thức là {M_{\min }} = \frac{{32}}{5} khi x = z = 4 \Rightarrow \left( {x;y} ight) = \left( {4;2} ight)

  • Câu 28: Vận dụng cao
    Biểu thức liên hệ giữa n và m

    Cho các số thực dương phân biệt a và b. Biểu thức thu gọn của biểu thức

    P = \frac{{\sqrt a - \sqrt b }}{{\sqrt[4]{a} - \sqrt[4]{b}}} - \frac{{\sqrt {4a} + \sqrt[4]{{16ab}}}}{{\sqrt[4]{a} + \sqrt[4]{b}}}

    có dạng P = m\sqrt[4]{a} + n\sqrt[4]{b}. Khi đó biểu thức liên hệ giữa n và m là:

    Hướng dẫn:

    Ta có:

    \begin{matrix} P = \dfrac{{\sqrt a - \sqrt b }}{{\sqrt[4]{a} - \sqrt[4]{b}}} - \dfrac{{\sqrt {4a} + \sqrt[4]{{16ab}}}}{{\sqrt[4]{a} + \sqrt[4]{b}}} \hfill \\ P = \dfrac{{{{\left( {\sqrt[4]{a}} ight)}^2} - {{\left( {\sqrt[4]{b}} ight)}^2}}}{{\sqrt[4]{a} - \sqrt[4]{b}}} - \dfrac{{2\sqrt[4]{a}\sqrt[4]{a} + 2\sqrt[4]{a}\sqrt[4]{b}}}{{\sqrt[4]{a} + \sqrt[4]{b}}} \hfill \\ P = \dfrac{{\left( {\sqrt[4]{a} - \sqrt[4]{b}} ight)\left( {\sqrt[4]{a} + \sqrt[4]{b}} ight)}}{{\sqrt[4]{a} - \sqrt[4]{b}}} - \dfrac{{2\sqrt[4]{a}\left( {\sqrt[4]{a} + \sqrt[4]{b}} ight)}}{{\sqrt[4]{a} + \sqrt[4]{b}}} \hfill \\ P = \sqrt[4]{a} + \sqrt[4]{b} - 2\sqrt[4]{a} = \sqrt[4]{b} - \sqrt[4]{a} \hfill \\ \Rightarrow m = - 1;n = 1 \hfill \\ \end{matrix}

  • Câu 29: Vận dụng
    Khẳng định nào sau đây đúng?

    Cho biết {\left( {x - 2} ight)^{ - \frac{1}{3}}} > {\left( {x - 2} ight)^{ - \frac{1}{6}}}, khẳng định nào sau đây đúng?

    Hướng dẫn:

    Điều kiện: x - 2 > 0 \to x > 2

    Ta có:

    - \frac{1}{3} > - \frac{1}{6} \Rightarrow {\left( {x - 2} ight)^{ - \frac{1}{3}}} > {\left( {x - 2} ight)^{ - \frac{1}{6}}}

    \Rightarrow x - 2 < 1 \Rightarrow x < 3

    Vậy 2 < x < 3

  • Câu 30: Thông hiểu
    Tính giá trị của biểu thức logarit

    Với các số a, b, c là các số thực dương tùy ý khác 1 và {\log _a}c = x;{\log _b}c = y. Khi đó giá trị của {\log _a}\left( {ab} ight) bằng:

    Hướng dẫn:

     Với a, b, c là các số thực dương tùy ý khác 1 ta có: {\log _c}a = \frac{1}{x};{\log _c}b = \frac{1}{y}

    Khi đó ta có: {\log _c}\left( {ab} ight) = {\log _c}a + {\log _c}b = \frac{1}{x} + \frac{1}{y}

0/30
30 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (20%):
    2/3
  • Thông hiểu (30%):
    2/3
  • Vận dụng (20%):
    2/3
  • Vận dụng cao (30%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 1 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập