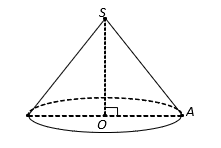
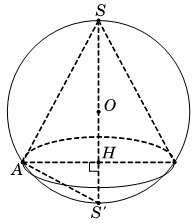
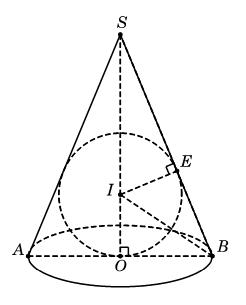
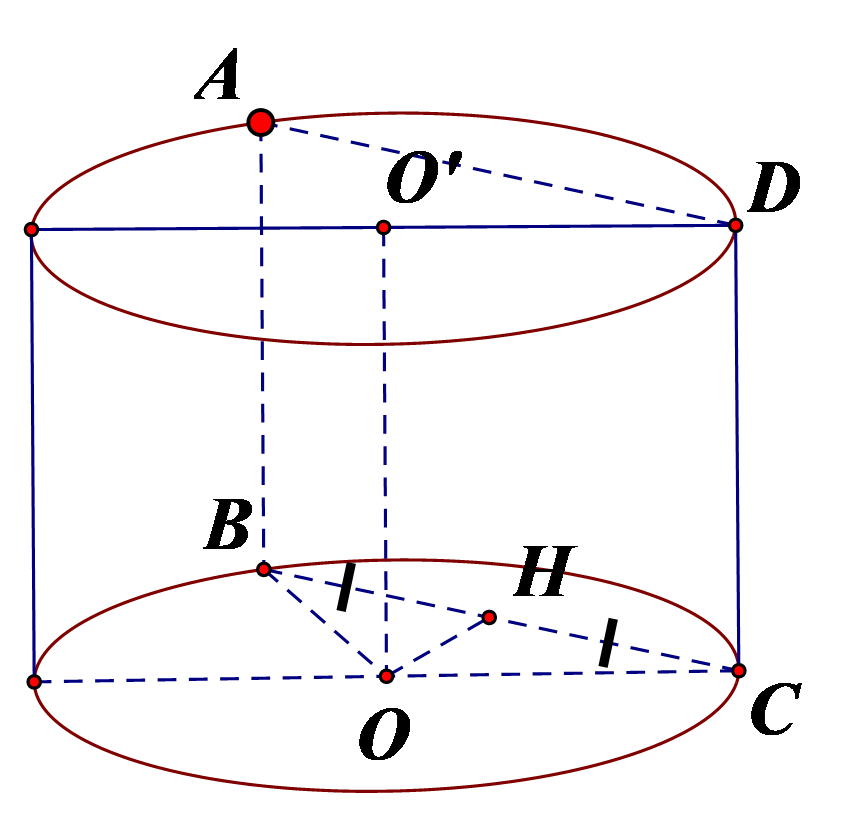
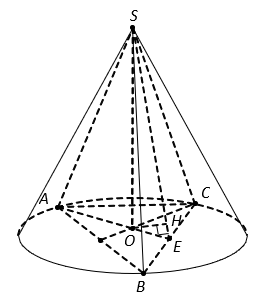
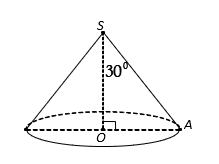
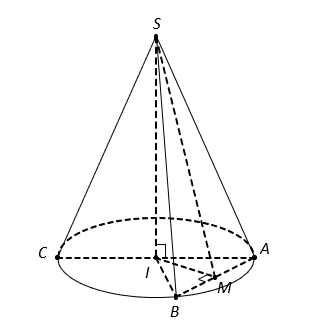
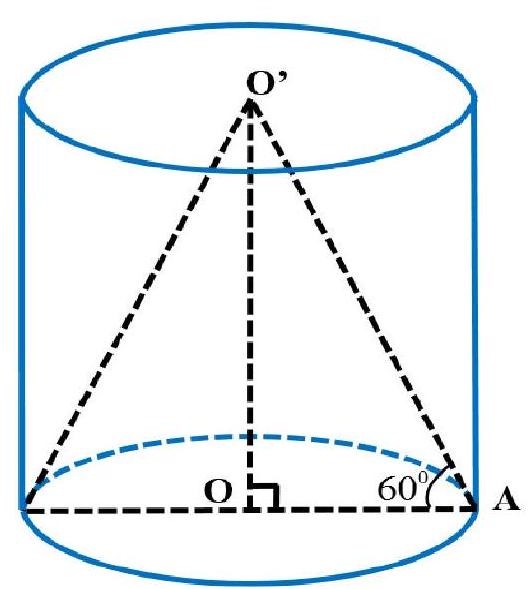
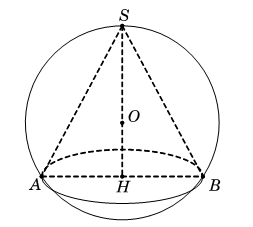
Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là một tam giác vuông ![]() có diện tích bằng
có diện tích bằng ![]() . Góc giữa trục
. Góc giữa trục ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() . Diện tích xung quanh của hình nón đã cho bằng?
. Diện tích xung quanh của hình nón đã cho bằng?
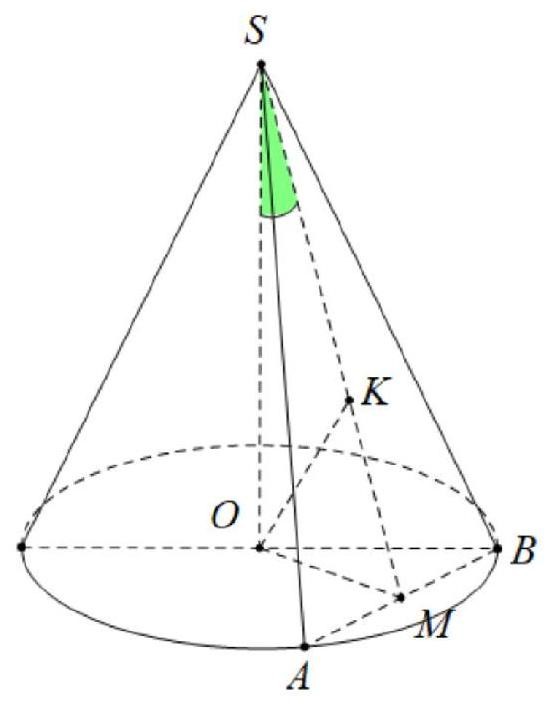
Gọi là trung điểm của
, tam giác
cân đỉnh O nên
và
suy ra
Dựng .
Theo trên có nên
.
Vậy góc tạo bởi giữa trục và mặt phẳng
là
. Tam giác vuông cân
có diện tích bằng
suy ra
.
Xét tam giác vuông có
.
Cuối cùng .
Vậy diện tích xung quanh của hình nón bằng .