Phương trình mặt cầu
Bài học Lí thuyết toán 12: Phương trình mặt cầu bao gồm các dạng phương trình mặt cầu, vị trí tương đối giữa mặt cầu và mặt phẳng, đường thẳng. Bên cạnh đó, bài học kèm theo một số ví dụ bài tập có hướng dẫn giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia.
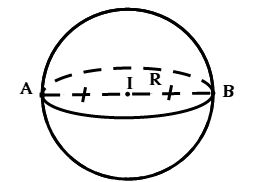
1. Khái niệm mặt cầu
Cho điểm ![]() cố định và một số thực dương
cố định và một số thực dương ![]() . Tập hợp tất cả những điểm
. Tập hợp tất cả những điểm ![]() trong không gian cách
trong không gian cách ![]() một khoảng
một khoảng ![]() được gọi là mặt cầu tâm
được gọi là mặt cầu tâm ![]() , bán kính
, bán kính ![]() .
.
Kí hiệu:
![]()
2. Các dạng phương trình mặt cầu
Dạng 1: Phương trình chính tắc
Mặt cầu ![]() có tâm
có tâm ![]() , bán kính
, bán kính ![]() có phương trình là:
có phương trình là:
![]()
Ví dụ: Viết phương trình mặt cầu ![]() , trong các trường hợp sau:
, trong các trường hợp sau:
a) ![]() có tâm
có tâm ![]() và bán kính
và bán kính ![]()
Giải:
Mặt cầu ![]() tâm
tâm ![]() và bán kính
và bán kính ![]() , có phương trình:
, có phương trình:![]()
b) ![]() qua
qua ![]() và tâm
và tâm ![]() thuộc trục
thuộc trục ![]() .
.
Giải:
Gọi ![]() . Ta có:
. Ta có: ![]()
Do ![]() đi qua A, B
đi qua A, B ![]()
![]()
![]() và
và ![]() .
.
Mặt cầu tâm ![]() và bán kính
và bán kính ![]() , có phương trình (S):
, có phương trình (S):![]()
Dạng 2: Phương trình tổng quát
Mặt cầu ![]() có tâm
có tâm ![]() có phương trình là:
có phương trình là:
![]()
- Điều kiện để có phương trình mặt cầu là:
![]()
 có tâm
có tâm 
 có bán kính:
có bán kính: 
Ví dụ:
Viết phương trình mặt cầu ![]() biết :
biết :
![]() qua bốn điểm
qua bốn điểm ![]() .
.
Giải:
Gọi phương trình mặt cầu ![]() :
: ![]() ,
, ![]() .
.
Do ![]()
![]() (1)
(1)
Tương tự:
![]() (2)
(2)
![]()
![]() (3)
(3)
![]() (4)
(4)
Giải hệ (1), (2), (3), (4) ta có ![]() , suy ra phương trình mặt cầu
, suy ra phương trình mặt cầu ![]() :
: ![]()
![]()
hay ![]()
3. Vị trí tương đối
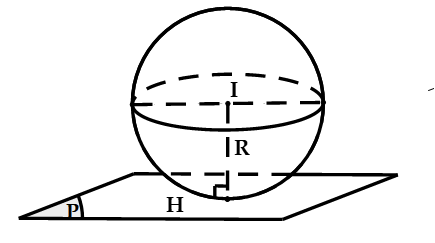
3.1. VTTĐ giữa mặt cầu và mặt phẳng :
Cho mặt cầu ![]() và mặt phẳng
và mặt phẳng ![]() . Gọi H là hình chiếu vuông góc của I lên
. Gọi H là hình chiếu vuông góc của I lên ![]()
![]() là khoảng cách từ I đến mặt phẳng
là khoảng cách từ I đến mặt phẳng ![]() . Khi đó :
. Khi đó :
+ Nếu ![]() : Mặt cầu và mặt phẳng không có điểm chung.
: Mặt cầu và mặt phẳng không có điểm chung.

+ Nếu ![]() : Mặt phẳng tiếp xúc mặt cầu. Lúc đó:
: Mặt phẳng tiếp xúc mặt cầu. Lúc đó: ![]() là mặt phẳng tiếp diện của mặt cầu và H là tiếp điểm.
là mặt phẳng tiếp diện của mặt cầu và H là tiếp điểm.
+ Nếu ![]() : Mặt phẳng
: Mặt phẳng ![]() cắt mặt cầu theo thiết diện là đường tròn có tâm I' và bán kính
cắt mặt cầu theo thiết diện là đường tròn có tâm I' và bán kính ![]()
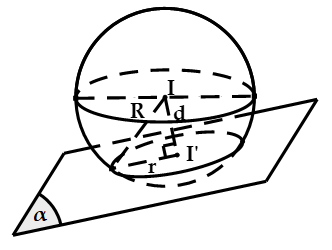
Lưu ý: Khi mặt phẳng (P) đi qua tâm I thì mặt phẳng (P) được gọi là mặt phẳng kính và thiết diện lúc đó được gọi là đường tròn lớn.
Ví dụ: Viết phương trình mặt cầu (S) có tâm O và tiếp xúc mặt phẳng: ![]()
Giải:
Do (S) tiếp xúc với ![]()
![]()
Mặt cầu tâm ![]() và bán kính
và bán kính ![]() , có phương trình (S) :
, có phương trình (S) : ![]()
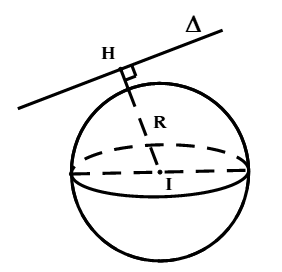
3.2. VTTĐ giữa mặt cầu và đường thẳng
Cho mặt cầu ![]() và đường thẳng
và đường thẳng ![]() . Gọi H là hình chiếu của I lên
. Gọi H là hình chiếu của I lên ![]() . Khi đó :
. Khi đó :
+ ![]() :
: ![]() không cắt mặt cầu.
không cắt mặt cầu.
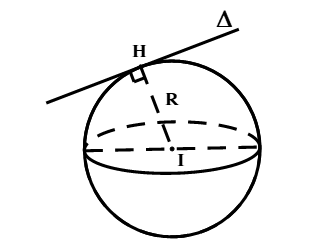
+ ![]() :
: ![]() tiếp xúc với mặt cầu.
tiếp xúc với mặt cầu. ![]() là tiếp tuyến của (S) và H là tiếp điểm.
là tiếp tuyến của (S) và H là tiếp điểm.
+ ![]() :
: ![]() cắt mặt cầu tại hai điểm phân biệt.
cắt mặt cầu tại hai điểm phân biệt.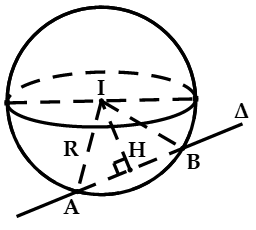
* Lưu ý: Trong trường hợp ![]() cắt (S) tại 2 điểm A, B thì bán kính R của (S) được tính như sau:
cắt (S) tại 2 điểm A, B thì bán kính R của (S) được tính như sau:
+ Xác định: ![]()
+ Lúc đó: 
4. Đường tròn giao tuyến
Cho đường tròn ![]() trong không gian
trong không gian ![]() , được xem là giao tuyến của
, được xem là giao tuyến của ![]() và mặt phẳng
và mặt phẳng ![]() .
.
![]()
![]()
* Xác định tâm  và bán kính
và bán kính  của
của  .
.
+ Tâm ![]() .
.
Trong đó d là đường thẳng đi qua I và vuông góc với mp ![]()
+ Bán kính ![]()
* Điều kiện tiếp xúc:
Cho mặt cầu (S) tâm I, bán kính R.
+ Đường thẳng ![]() là tiếp tuyến của (S)
là tiếp tuyến của (S) ![]()
![]()
+ Mặt phẳng ![]() là tiếp diện của (S)
là tiếp diện của (S) ![]()
![]()
Lưu ý: Để tìm tiếp điểm ![]() , sử dụng tính chất:
, sử dụng tính chất:
 Ví dụ:
Ví dụ:
Chứng minh rằng: Mặt cầu ![]() cắt mặt phẳng
cắt mặt phẳng ![]() :
:![]() theo giao tuyến là một đường tròn
theo giao tuyến là một đường tròn ![]() .
.
Xác định tâm và bán kính của ![]() .
.
Giải:
* Mặt cầu ![]() có tâm
có tâm ![]() và bán kính
và bán kính ![]() .
.
Ta có : ![]() mặt phẳng
mặt phẳng ![]() cắt
cắt ![]() theo giao tuyến là 1 đường tròn. (đpcm)
theo giao tuyến là 1 đường tròn. (đpcm)
* Đường thẳng d qua ![]() và vuông góc với
và vuông góc với ![]() nên nhận
nên nhận ![]() làm 1 vectơ chỉ phương, có phương trình:
làm 1 vectơ chỉ phương, có phương trình:  .
.
+ Tọa độ tâm I đường tròn là nghiệm của hệ :  .
.
+ Ta có: ![]() .
.
Gọi r là bán kính của ![]() , ta có :
, ta có : ![]()
Nội dung cùng chủ đề
-
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
Chương 2: Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
Chương 3: Nguyên hàm - Tích phân và ứng dụng
-
Chương 4: Số phức
-
Chương 1 Hình: Khối đa diện
-
Chương 2 Hình: Mặt nón, mặt trụ, mặt cầu
-
Chương 3: Phương pháp tọa độ trong không gian
-
Ôn thi Học kì







