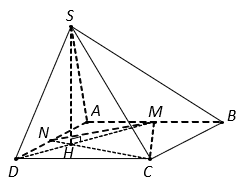
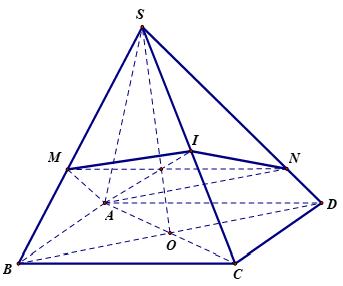
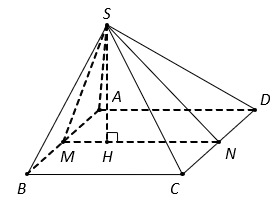
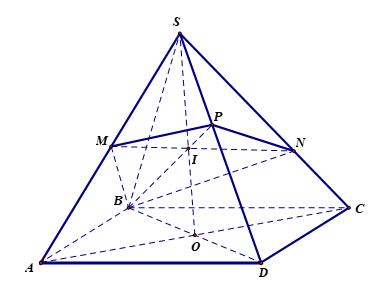
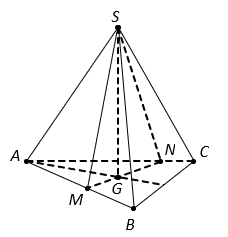
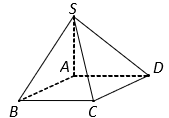
Cho hình chóp ![]() có thể tích bằng
có thể tích bằng ![]() , đáy
, đáy ![]() là hình vuông;
là hình vuông; ![]() và
và ![]() hợp với đáy một góc bằng
hợp với đáy một góc bằng ![]() . Mặt phẳng
. Mặt phẳng ![]() đi qua A và vuông góc với
đi qua A và vuông góc với ![]() , cắt các cạnh
, cắt các cạnh ![]() lần lượt tại
lần lượt tại ![]() . Tính thể tích khối chóp
. Tính thể tích khối chóp ![]() .
.
V/10 || V phần 10
Cho hình chóp có thể tích bằng
, đáy
là hình vuông;
và
hợp với đáy một góc bằng
. Mặt phẳng
đi qua A và vuông góc với
, cắt các cạnh
lần lượt tại
. Tính thể tích khối chóp
.
V/10 || V phần 10
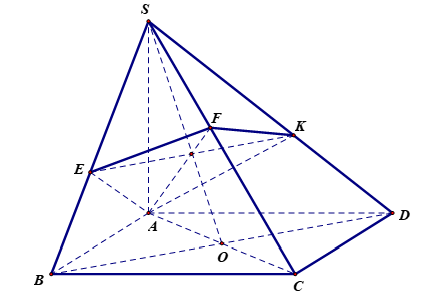
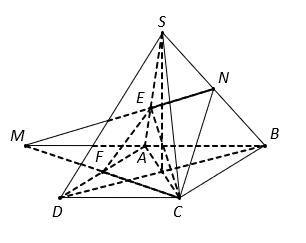
Ta có . Tương tự
nên
.
Mà (do
vuông tại A,
) nên ta có:
Xét tỉ số thể tích, ta được: