Hướng dẫn:
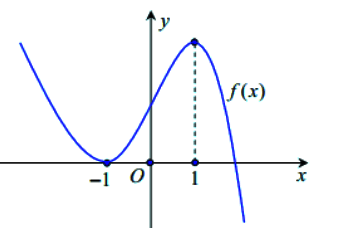
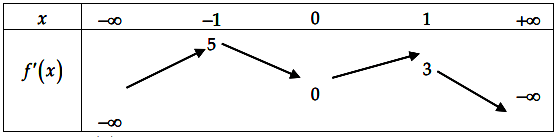
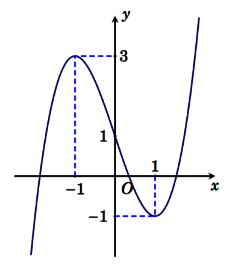
Xét hàm số %20%3D%20f%5Cleft(%20%7B%7Bx%5E3%7D%20-%20m%7Bx%5E2%7D%20-%202x%20%2B%20m%7D%20%5Cright))
%20%3D%20%5Cleft(%20%7B3%7Bx%5E2%7D%20-%202mx%20-%202%7D%20%5Cright).f'%5Cleft(%20%7B%7Bx%5E3%7D%20-%20m%7Bx%5E2%7D%20-%202x%20%2B%20m%7D%20%5Cright))
Yêu cầu bài toán xảy ra khi phương trình đạo hàm phải có 6 nghiệm bội lẻ:
Ta có:
%20%3D%200%20%5CLeftrightarrow%20%5Cleft%5B%20%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D%0A%20%20%7B3%7Bx%5E2%7D%20-%202mx%20-%202%20%3D%200%7D%20%5C%5C%20%0A%20%20%7Bf'%5Cleft(%20%7B%7Bx%5E3%7D%20-%20m%7Bx%5E2%7D%20-%202x%20%2B%20m%7D%20%5Cright)%20%3D%200%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.%20%5CLeftrightarrow%20%5Cleft%5B%20%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D%0A%20%20%7B3%7Bx%5E2%7D%20-%202mx%20-%202%20%3D%200%5Cleft(%20*%20%5Cright)%7D%20%5C%5C%20%0A%20%20%5Cbegin%7Bgathered%7D%0A%20%20%7Bx%5E3%7D%20-%20m%7Bx%5E2%7D%20-%202x%20%2B%20m%20%3D%20%20-%201%7B%5Ctext%7B%20%20%7D%7D%20%5Chfill%20%5C%5C%0A%20%20%7Bx%5E3%7D%20-%20m%7Bx%5E2%7D%20-%202x%20%2B%20m%20%3D%201%7B%5Ctext%7B%20%20%20%20%7D%7D%20%5Chfill%20%5C%5C%20%0A%5Cend%7Bgathered%7D%20%20%0A%5Cend%7Barray%7D%7D%20%5Cright.)
Phương trình (*) luôn có hai nghiệm phân biệt => Hai phương trình còn lại phải cho đúng 4 nghiệm nghiệm bội lẻ.
![\left[ {\begin{array}{*{20}{c}} {{x^3} - m{x^2} - 2x + m = - 1{\text{ }}} \\ {{x^3} - m{x^2} - 2x + m = 1{\text{ }}} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\left( {x - 1} ight)\left[ {{x^2} - \left( {m - 1} ight)x - m - 1} ight] = 0{\text{ }}\left( 1 ight)} \\ {\left( {x - 1} ight)\left[ {{x^2} - \left( {m + 1} ight)x + m - 1} ight] = 0{\text{ }}\left( 2 ight)} \end{array}} ight.](https://tex.vdoc.vn?tex=%5Cleft%5B%20%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D%0A%20%20%7B%7Bx%5E3%7D%20-%20m%7Bx%5E2%7D%20-%202x%20%2B%20m%20%3D%20%20-%201%7B%5Ctext%7B%20%7D%7D%7D%20%5C%5C%20%0A%20%20%7B%7Bx%5E3%7D%20-%20m%7Bx%5E2%7D%20-%202x%20%2B%20m%20%3D%201%7B%5Ctext%7B%20%7D%7D%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.%20%5CLeftrightarrow%20%5Cleft%5B%20%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D%0A%20%20%7B%5Cleft(%20%7Bx%20-%201%7D%20%5Cright)%5Cleft%5B%20%7B%7Bx%5E2%7D%20-%20%5Cleft(%20%7Bm%20-%201%7D%20%5Cright)x%20-%20m%20-%201%7D%20%5Cright%5D%20%3D%200%7B%5Ctext%7B%20%20%20%7D%7D%5Cleft(%201%20%5Cright)%7D%20%5C%5C%20%0A%20%20%7B%5Cleft(%20%7Bx%20-%201%7D%20%5Cright)%5Cleft%5B%20%7B%7Bx%5E2%7D%20-%20%5Cleft(%20%7Bm%20%2B%201%7D%20%5Cright)x%20%2B%20m%20-%201%7D%20%5Cright%5D%20%3D%200%7B%5Ctext%7B%20%20%20%20%7D%7D%5Cleft(%202%20%5Cright)%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.)
Nhận thấy hai phương trình (1), (2) luôn cho hai nghiệm phân biệt vafcacs nghiệm của hai phương trình này không trùng nhau.
Để hai phương trình có đúng 4 nghiệm bội lẻ thì:
TH1: x = 1 là nghiệm của (x – 1)[x2 – (m – 1)x – m – 1] = 0 và x = -1 không phải là nghiệm của (x – 1)[x2 – (m + 1)x + m – 1] = 0
TH2: x = -1 là nghiệm của (x – 1)[x2 – (m + 1)x + m – 1] = 0 và x = 1 không phải là nghiệm của (x – 1)[x2 – (m – 1)x - m – 1] = 0
=> %20-%20m%20-%201%20%3D%200%7D%20%5C%5C%20%0A%20%20%7B1%20%2B%20%5Cleft(%20%7Bm%20%2B%201%7D%20%5Cright)%20%2B%20m%20-%201%20%5Cne%200%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.%7D%20%5C%5C%20%0A%20%20%7B%5Cleft%5C%7B%20%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D%0A%20%20%7B1%20-%20%5Cleft(%20%7Bm%20-%201%7D%20%5Cright)%20-%20m%20-%201%20%5Cne%200%7D%20%5C%5C%20%0A%20%20%7B1%20%2B%20%5Cleft(%20%7Bm%20%2B%201%7D%20%5Cright)%20%2B%20m%20-%201%20%3D%200%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.%5Cleft%5B%20%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D%0A%20%20%7B%5Cleft%5C%7B%20%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D%0A%20%20%7Bm%20%3D%20%5Cdfrac%7B1%7D%7B2%7D%7D%20%5C%5C%20%0A%20%20%7Bm%20%5Cne%20%20-%20%5Cdfrac%7B1%7D%7B2%7D%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.%7D%20%5C%5C%20%0A%20%20%7B%5Cleft%5C%7B%20%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D%0A%20%20%7Bm%20%5Cne%20%5Cdfrac%7B1%7D%7B2%7D%7D%20%5C%5C%20%0A%20%20%7Bm%20%3D%20%20-%20%5Cdfrac%7B1%7D%7B2%7D%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.%7D%20%0A%5Cend%7Barray%7D%7D%20%5Cright.%20%5CRightarrow%20m%20%5Cpm%20%5Cfrac%7B1%7D%7B2%7D)
Vậy có hai giá thực của m thỏa mãn
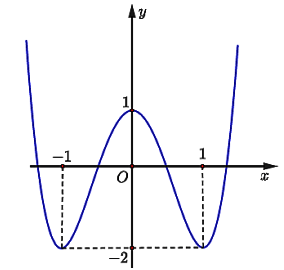
![]() . Bán kính của đường tròn nội tiếp tam giác ABC bằng:
. Bán kính của đường tròn nội tiếp tam giác ABC bằng: có ba điểm cực trị là A(0; 4), B(1; 3), C(-1;; 3)