Đồ thị hàm số nào sau đây không có tiệm cận ngang?
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có:
Vậy đồ thị hàm số không có tiệm cận ngang.
Đồ thị hàm số nào sau đây không có tiệm cận ngang?
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có:
Vậy đồ thị hàm số không có tiệm cận ngang.
Tìm tập hợp các giá trị thực của m để đồ thị hàm số ![]() có tiệm cận đứng là:
có tiệm cận đứng là:
Để tồn tại các đường tiệm cận của đồ thị hàm số thì
Khi đó phương trình đường tiệm cận đứng là
Điều kiện để đồ thị hàm số có tiệm cận là
ho hàm số  . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đồ thị hàm số có hai đường tiệm cận đứng là x = 1 và x = -1 và một tiệm cận ngang là y = -1
Cho hàm số ![]() có bảng biến thiên như hình vẽ dưới đây.
có bảng biến thiên như hình vẽ dưới đây.
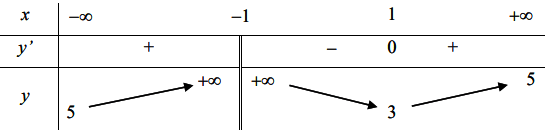
Số đường tiệm cận của đồ thị hàm số ![]() là:
là:
Đường thẳng là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Phương trình có 2 nghiệm phân biệt
=> Đồ thị hàm số có 2 đường tiệm cận đứng.
Khi thì
Khi thì
Vậy đồ thị hàm số có 1 tiệm cận ngang.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây
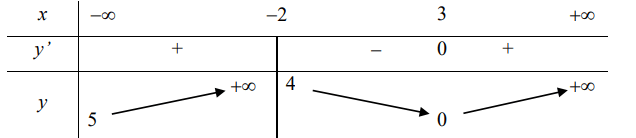
Số đường tiệm cận của đồ thị hàm số y = f(x) là
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Dựa vào bảng biến thiên ta thấy
=> x = -2 là tiệm cận đúng của đồ thị hàm số
Ta cũng có = > y = 5 là tiệm cận ngang của đồ thị hàm số
Do đó đồ thị hàm số có 2 đường tiệm cận
Cho hàm số xác định trên và có bảng biến thiên như hình vẽ:
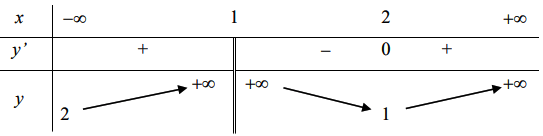
Số đường tiệm cận đứng của đồ thị hàm số ![]() là:
là:
Đường thẳng là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có:
Phương trình có 3 nghiệm phân biệt khác 2.
Phương trình có một nghiệm kép là x = 2 (do vậy mẫu số có dạng
nên x = 2 vẫn là TCĐ của đồ thị hàm số
=> Đồ thị hàm số có 4 đường tiệm cận đứng.
Cho hàm số | 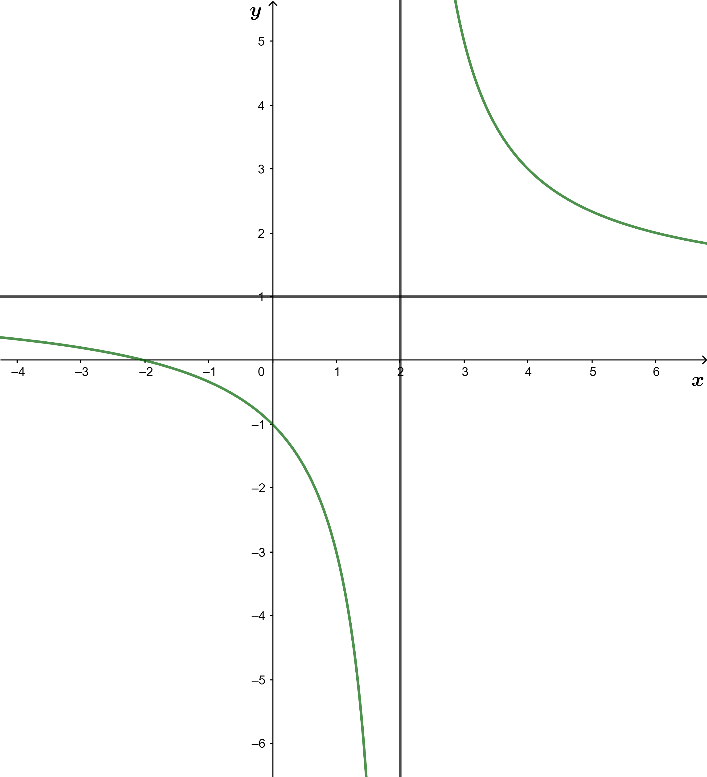 |
Dựa vào đồ thị hàm số để xác định nghiệm của mẫu số và tử số từ đó suy ra các đường tiệm cận đứng của đồ thị hàm số.
Tìm các giới hạn để tìm các đường tiệm cận ngang của đồ thị hàm số.
Từ đồ thị hàm số ta có nhận xét như sau:
Đường thẳng x = 2 là tiệm cận đứng của đồ thị (C)
=>
Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số (C)
=>
Điểm có tọa độ (0; -1) thuộc đồ thị hàm số (C)
=> y(0) = -1 =>
=>
Số đường tiệm cận của đồ thị hàm số ![]()
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Quy đồng biến đổi hàm số đã cho trở thành
Tìm được tiệm cận đứng là x = -1 và x = 4 và không có tiệm cận ngang
=> Số tiệm cận là 2 đường
Cho hàm số ![]() . Biết đồ thị hàm số đã cho đi qua điểm
. Biết đồ thị hàm số đã cho đi qua điểm ![]() và có đường tiệm cận ngang là
và có đường tiệm cận ngang là ![]() . Giá trị
. Giá trị ![]() bằng:
bằng:
Để tồn tại các đường tiệm cận của đồ thị hàm số thì
Khi đó phương trình đường tiệm cận ngang là
Điều kiện để đồ thị hàm số có tiệm cận là
=> Đồ thị hàm số đi qua điểm nên
Đồ thị hàm số có đường tiệm cận ngang là (thỏa mãn)
Vậy
Cho hàm số ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có tiệm cận đứng của hàm số là y = 3 và tiệm cận ngang là y = 1
Giao điểm của hai đường tiệm cận I(3; 1) là tâm đối xứng của đồ thị
=> A, C, D đúng và B sai
Đồ thị hàm số ![]() có bao nhiêu đường tiệm cận?
có bao nhiêu đường tiệm cận?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Tập xác định:
Ta có: => y = 1 và y = -1 là hai tiệm cận ngang của đồ thị hàm số.
=> Đồ thị hàm số có hai tiệm cận đứng là x = 2 và x = =-2
Vậy đồ thị hàm số đã cho có 2 tiệm cận đứng là x = 2 và x = -2
Cho hàm số y = f(x) có ![]() và
và ![]() . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có: => Đồ thị hàm số đã cho có TCĐ là x = 0
=> Đồ thị hàm số đã cho có TCĐ là x = 2
Đồ thị hàm số nào sau đây không có tiệm cận đứng?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Phương trình x2 + 1 = 0 vô nghiệm nên không tìm được x0 để
=> Hàm số không có tiệm cận đứng.
Các đồ thị hàm số ở B, C, D lần lượt có các tiệm cận đứng là x = 0, x = -2 và x = 1
Đồ thị hàm số nào sau đây có ba đường tiệm cận?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có: Đồ thị hàm số có 3 đường tiệm cận trong đó
Tiệm cận đứng là x = 2 và x = -2
Tiệm cận ngang là y = 0
Tìm giá trị của tham số m sao cho đồ thị hàm số ![]() có tiệm cận ngang.
có tiệm cận ngang.
Ta có:
Đồ thị hàm số có tiệm cận ngang khi và chỉ khi bậc của tử số bé hơn hoặc bằng bậc của mẫu số
Đồng thời
Cho hàm số ![]() . Đồ thị hàm số có mấy đường tiệm cận?
. Đồ thị hàm số có mấy đường tiệm cận?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Tập xác định:
Ta thấy rằng x = 1 không thuộc D => Đồ thị hàm số không có tiệm cận đứng.
=> y = 1 và y = -1 là hai tiệm cận ngang của đồ thị hàm số.
Cho hàm số ![]() . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có hai tiệm cận đứng.
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có hai tiệm cận đứng.
Ta có:
Đồ thị hàm số có hai tiệm cận đứng khi và chỉ khi phương trình có hai nghiệm phân biệt thỏa mãn
Cho đồ thị hàm số như hình vẽ dưới đây:
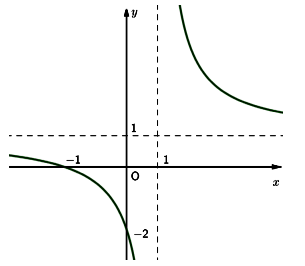
Đồ thị hàm số tương ứng với hàm số nào sau đây?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Từ đồ thị hàm số ta có tiệm cận đứng là x = 1, tiệm cận ngang là y = 1
=> Loại A và B
Xét thấy giao điểm của đồ thị hàm số với trục tung là (0; -2) => Chọn đáp án C
Giá trị của tham số m để đồ thị hàm số ![]() có đường tiệm cận ngang
có đường tiệm cận ngang ![]() là:
là:
Để tồn tại các đường tiệm cận của đồ thị hàm số thì
Khi đó phương trình đường tiệm cận ngang là
Điều kiện để đồ thị hàm số có tiệm cận là:
luôn đúng với
Phương trình đường tiệm cận ngang là nên ta có
Cho hàm số ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có:
=> y = 2 là tiệm cận ngang của đồ thị hàm số
Ta cũng có: => x = 1; x = 32 là tiệm cận đứng của đồ thị hàm số
