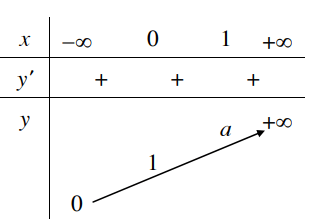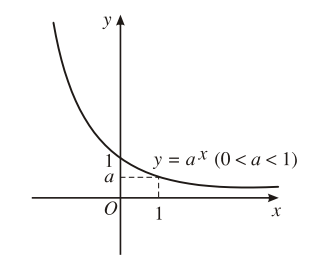Lớp 12 Toán 12

Hàm số mũ

Bài học Lí thuyết toán 12: Hàm số mũ giới thiệu cho các em khái niệm về hàm số mũ, công thức tính đạo hàm của hàm số mũ và khảo sát hàm số mũ y=a^x. Bên cạnh đó là các ví dụ bài tập có lời giải chi tiết giúp các em dễ dàng ôn tập củng cố.

1. Định nghĩa

Cho số thực dương a \ne 1. Hàm số y=a^x được gọi là hàm số mũ cơ số a

Ví dụ: (\sqrt 3 )^x là hàm số mũ cơ số \sqrt 3.

2. Công thức đạo hàm

Hàm số  y=e^x có đạo hàm tại mọi x :

\boxed{(e^x)'=e^x}

Ngoài ra, ta có công thức đạo hàm đối với hàm hợp  y=e^u (u=u(x)) là:

\boxed{(e^u)'=u'.e^u}

Hàm số y=a^x (a>0, a \ne 1) có đạo hàm tại mọi x:

\boxed{(a^x)'=a^xlna }

Ngoài ra, ta có công thức đạo hàm đối với hàm hợp y=a^{u(x)} là:

\boxed{(a^u)'=a^ulna.u'}

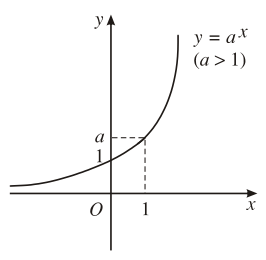
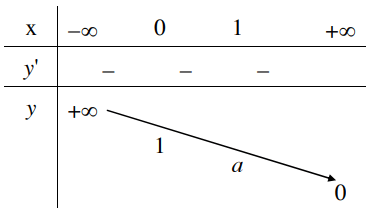
3. Khảo sát hàm số mũ y=a^x (a>0, a \ne 1)

y = {a^x},\left( {a > 1} \right)

y = {a^x},\left( {a < 1} \right)

1. Tập xác định: \mathbb{R}

2. Sự biến thiên

y' = {a^x}\ln a > 0,\forall x

Giới hạn đặc biệt:

\mathop {\lim }\limits_{x \to - \infty } {a^x} = 0,\begin{array}{*{20}{c}} {}&{\mathop {\lim }\limits_{x \to + \infty } } \end{array}a = + \infty .

Tiệm cận:

Ox là tiệm cận ngang

3. Bảng biến thiên

Đồ thị hàm số:

Đồ thị luôn đi qua các điểm (0;1) và  (1;a) nằm phía trên trục hoành.

1. Tập xác định: \mathbb{R}

2. Sự biến thiên

y' = {a^x}\ln a < 0,\forall x

Giới hạn đặc biệt:

\mathop {\lim }\limits_{x \to - \infty } {a^x} = + \infty ,\begin{array}{*{20}{c}} {}&{\mathop {\lim }\limits_{x \to + \infty } } \end{array}{a^x} = 0.

Tiệm cận:

Ox là tiệm cận ngang

3. Bảng biến thiên

Đồ thị hàm số:

Đồ thị luôn đi qua các điểm (0;1) và (1;a) nằm phía trên trục hoành.

4. Bài toán lãi kép

4.1.  Định nghĩa

Lãi kép là phần lãi của kì sau được tính trên số tiền gốc kì trước cộng với phần lãi của kì trước.

4.2. Công thức:

Giả sử số tiền gốc là A; lãi suất  r\%/kì hạn gửi (có thể là tháng, quý hay năm).

  • Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là:

  \boxed{A{{\left( {1 + r} \right)}^n}}

  • Số tiền lãi nhận được sau n kì hạn gửi là:

\boxed{A{{\left( {1 + r} \right)}^n} - A = A\left[ {{{\left( {1 + r} \right)}^n} - 1} \right]}

Ví dụ: Bà Hoa gửi 100 triệu vào tài khoản định kỳ tính lãi kép với lãi suất là 8%/năm. Tính số tiền lãi thu được sau 10 năm.

Giải:

Áp dụng công thức tính lãi kép, sau 10 năm số tiền cả gốc và lãi bà Hoa thu về là:

A{\left( {1 + r} \right)^n} = 100{\text{tr}}.{\left( {1 + 0,08} \right)^{10}} \approx 215,892{\text{tr}}.

Suy ra số tiền lãi bà Hoa thu về sau 10 năm là:

A{\left( {1 + r} \right)^n} - A \approx 215,892{\text{tr}} - 100{\text{tr}} = 115,892{\text{tr}}.

Câu trắc nghiệm mã số: 2112, 2111, 2121
  • 14 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12