Lớp 12 Toán 12

Đề Ôn tập chương 1: Khối đa diện (Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 30 câu
  • Điểm số bài kiểm tra: 30 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng cao
    Giá trị lớn nhất của biểu thức

    Cho số phức z thỏa mãn \left| {i.z + 3} ight| = \sqrt {\frac{5}{2}}. Giá trị lớn nhất của biểu thức P = \left| {2{\text{z}} + 1 - 4i} ight| + \left| {z - 1 - 5i} ight| là:

    Hướng dẫn:

    Ta gọi M(x;y) là điểm biểu diễn số phức z

    \left| {i.z + 3} ight| = \sqrt {\frac{5}{2}} \Leftrightarrow {x^2} + {\left( {y - 3} ight)^2} = \frac{5}{2}

    => M(x;y) \in C\left( {I(0;3);R = \sqrt {\frac{5}{2}} } ight)

    Khi đó:

    \begin{matrix} P = \left| {2{\text{z}} + 1 - 4i} ight| + \left| {z - 1 - 5i} ight| \hfill \\ = 2\left| {{\text{z}} + \frac{1}{2} - 2i} ight| + \left| {z - 1 - 5i} ight| \hfill \\ = 2\left| {\overrightarrow {MA} } ight| + \left| {\overrightarrow {MB} } ight| \hfill \\ \end{matrix}

    với A\left( { - \frac{1}{2};2} ight);B\left( {1;5} ight)

    Ta có: \overrightarrow {IA} = \left( { - \frac{1}{2}; - 1} ight),;\overrightarrow {IB} = \left( {1;2} ight) suy ra \overrightarrow {IB} = - 2.\overrightarrow {IA}.

    Theo định lý Stewart ta có:

    \sqrt 5 M{A^2} + \frac{{\sqrt 5 }}{2}M{B^2} = \frac{{3\sqrt 5 }}{2}\left( {M{I^2} + \frac{{\sqrt 5 }}{2}.\sqrt 5 } ight)

    \Rightarrow 2M{A^2} + M{B^2} = 15

    (Hoặc có thể chứng minh theo phương pháp véc tơ

    \overrightarrow {MI} = \overrightarrow {MA} + \overrightarrow {AB} = \overrightarrow {MA} + \frac{1}{3}\overrightarrow {AB} = \overrightarrow {MA} + \frac{1}{3}\left( {\overrightarrow {MB} - \overrightarrow {MA} } ight) = \frac{2}{3}\overrightarrow {MA} + \frac{1}{3}\overrightarrow {MB}

    Suy ra:

    \begin{matrix} M{I^2} = \dfrac{4}{9}M{A^2} + \dfrac{1}{9}M{B^2} + \dfrac{4}{9}MA.MB.cos\left( {\overrightarrow {MA} ,\overrightarrow {MB} } ight) \hfill \\ = \dfrac{4}{9}M{A^2} + \dfrac{1}{9}M{B^2} + \dfrac{4}{9}MA.MB.cos\widehat {AMB} \hfill \\ = \dfrac{4}{9}M{A^2} + \dfrac{1}{9}M{B^2} + \dfrac{4}{9}MA.MB\left( {\dfrac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} ight) \hfill \\ = \dfrac{2}{3}M{A^2} + \dfrac{1}{3}M{B^2} - \dfrac{2}{9}A{B^2} \hfill \\ \Rightarrow 2M{A^2} + M{B^2} = 3M{I^2} + \dfrac{2}{3}A{B^2} = 15 \hfill \\ \end{matrix}

    Khi đó suy ra:

    P = 2\left| {\overrightarrow {MA} } ight| + \left| {\overrightarrow {MB} } ight|

    = \left( {\sqrt {2.} \sqrt 2 .MA + MB} ight) \leqslant \sqrt {\left( {{{\sqrt 2 }^2} + {1^2}} ight)\left( {2M{A^2} + M{B^2}} ight)} = \sqrt {45} = 3\sqrt 5 .

  • Câu 2: Vận dụng cao
    Giá trị lớn nhất

    Cho số phức z thoả mãn |z+\overline{z}|+ |z-\overline{z}|=|z^2| . Giá trị lớn nhất của biểu thức P=|z-5-2i| bằng?

    Hướng dẫn:

    Đặt z=a+bi \,(a,b \in \mathbb R).

    Từ giả thiết |z+\overline{z}|+ |z-\overline{z}|=|z^2|

    \Leftrightarrow 2|a|+2|b|=a^2+b^2\Leftrightarrow(|a|-1)^2+(|b|-1)^2=2   (1).

    Ta có P=|z-5-2i| =\sqrt{ (a-5)^2+(b-2)^2}= \sqrt {2|a|+2|b|-10a-4b+29}.

    Dễ thấy P lớn nhất khi a, b \leq 0.

    Khi đó P=\sqrt {-12a-6b+29}=\sqrt{6[-2(a+1)-(b+1)]+47}

    Do a, b \leq 0 nên từ (1) ta có (a+1)^2+(b+1)^2=2.

    Suy ra P=\sqrt{6[-2(a+1)-(b+1)]+47} \leq \sqrt {6\sqrt{(2^2+1^2)[(a+1)^2+(b+1)^2]+47}}

    =\sqrt {47+6\sqrt{10}}==\sqrt {2} +3\sqrt 5

    Dấu = xảy ra khi \left\{\begin{matrix} (a+1)^2+(b+1)^2=2 \\ \dfrac{a+1}{2} =\dfrac{b+1}{1} \\ a+1, b+1 <0 \end{matrix}ight.  \Leftrightarrow \left\{\begin{matrix} a=-1-\dfrac{2\sqrt{10}}{5} \\ b=-1-\dfrac{\sqrt{10}}{5}\end{matrix}ight..

  • Câu 3: Vận dụng
    Tính giá trị biểu thức

    Cho số phức z = a + bi , \left( {a,b \in \mathbb{R}} ight)thỏa mãn \left( {z + 1 + i} ight)\left( {\overline z - i} ight) + 3i = 9 và \left| {\overline z } ight| > 2.

    Tính P = a + b.

    Hướng dẫn:

     Ta áp dụng công thức z = a + bi \Rightarrow \overline z = a - bi, có:

    \left( {z + 1 + i} ight)\left( {\overline z - i} ight) + 3i = 9

    \Leftrightarrow \left( {a + bi + 1 + i} ight)\left( {a - bi - i} ight) + 3i = 9

    \Leftrightarrow {a^2} + {b^2} + 2b + a + 1 - \left( {b + 1} ight)i = 9 - 3i

    Ta xét: \left\{ \begin{gathered} {a^2} + {b^2} + 2b + a + 1 = 9 \hfill \\ b + 1 = 3 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} b = 2 \hfill \\ {a^2} + a = 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} b = 2 \hfill \\ a = 0 \hfill \\ \end{gathered} ight. \vee \left\{ \begin{gathered} b = 2 \hfill \\ a = - 1 \hfill \\ \end{gathered} ight.

    Với {z_1} = 2i \Rightarrow \left| {{z_1}} ight| = 2 nên không thỏa yêu cầu bài toán.

    Với {z_2} = - 1 + 2i \Rightarrow \left| {{z_2}} ight| = \sqrt {{2^2} + {1^2}} = \sqrt 5 thỏa yêu cầu bài toán.

    Vậy P = a + b = 1

  • Câu 4: Nhận biết
    Số phức liên hợp của số phức 3 - 2i

    Số phức liên hợp của số phức 3 - 2i là

    Gợi ý:

     Cho số phức z = a + bi. Số phức \overline z = a – bi gọi là số phức liên hợp với số phức trên hay \overline z = \overline {a + bi} = a - bi

    Hướng dẫn:

     \overline z = \overline {a + bi} = a – bi

    \Rightarrow \overline z = \overline {3 - 2i} = 3 - ( - 2i) = 3 + 2i

  • Câu 5: Nhận biết
    Giá trị của số phức z

    Cho số phức z = 1 + 2i, giá trị của số phức w = z + i\overline z là?

    Hướng dẫn:

    Ta có: w = z + i\overline z = \left( {1 + 2i} ight) + i\left( {1 - 2i} ight) = 3 + 3i

  • Câu 6: Thông hiểu
    Căn bậc hai của số phức

    Tìm các căn bậc hai của số phức z = 5 + 12i

    Hướng dẫn:

     Giả sử m + ni (m; n \in R) là căn bậc hai của z

    Ta có: {(m + ni)^2} = 5 + 12i

    \Leftrightarrow {m^2} + 2mni + {n^2}{i^2} = 5 + 12i \Leftrightarrow {m^2} + 2mni - {n^2} = 5 + 12i

    \Leftrightarrow \left\{ \begin{gathered} {m^2} - {n^2} = 5 \hfill \\ 2mn = 12 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} {m^2} - {n^2} = 5(1) \hfill \\ m = \frac{6}{n}(2) \hfill \\ \end{gathered} ight.

    Thay (2) vào (1) ta có: {\left( {\frac{6}{n}} ight)^2} - {n^2} = 5 \Leftrightarrow 36 - {n^4} = 5{n^2}

    \Leftrightarrow {n^4} + 5{n^2} - 36 = 0 \Leftrightarrow {n^2} = 4;{n^2} = - 9(loai)

    \left[ \begin{gathered} n = 2 \Rightarrow m = 3 \hfill \\ n = - 2 \Rightarrow m = - 3 \hfill \\ \end{gathered} ight.

    Vậy z có hai căn bậc hai là 3+2i và -3-2i.

  • Câu 7: Thông hiểu
    Tìm x, y thỏa mãn điều kiện

    Tìm các số thực x, y thoả mãn:

    3x + y + 5xi = 2y – 1 +(x – y)i

    Hướng dẫn:

    Theo giả thiết: 3x + y + 5xi = 2y – 1 +(x – y)i

    => (3x + y) + (5x)i = (2y – 1) +(x – y)i

    =>\left\{ \begin{gathered} 3x + y = 2y - 1 \hfill \\ 5x = x - y \hfill \\ \end{gathered} ight.

    => \left\{ \begin{gathered} x = - \frac{1}{7} \hfill \\ y = \frac{4}{7} \hfill \\ \end{gathered} ight.

  • Câu 8: Nhận biết
    Chọn khẳng định sai?

    Cho số phức {\left( {\overline {2 + i} } ight)^5} - \left( {2 + i} ight).\overline z = - 37 - 43i. Khẳng định nào sau đây là khẳng định sai?

    Hướng dẫn:

     Ta có: {\left( {\overline {2 + i} } ight)^5} = - 38 - 41i \Rightarrow \overline z = \frac{{1 - 2i}}{{ - \left( {2 + i} ight)}} = i.

  • Câu 9: Vận dụng cao
    Tính giá trị nhỏ nhất của modun số phức

    Cho hai số phức {z_1};{z_2} thỏa mãn \left| {{z_1} + 5} ight| = 5\,;\,\left| {{z_2} + 1 - 3i} ight| = \left| {{z_2} - 3 - 6i} ight|. Tìm giá trị nhỏ nhất của \left| {{z_1} - {z_2}} ight|.

    Hướng dẫn:

    Gọi {z_1} = {a_1} + {b_1}i,\,\,\,{z_2} = {a_2} + {b_2}i\,\,\,({a_1},{b_1},{a_2},{b_2} \in \mathbb{R})

    Khi đó \left| {{z_1} + 5} ight| = 5 \Leftrightarrow {\left( {{a_1} + 5} ight)^2} + {b_1}^2 = 25

    Tập hợp điểm biểu diễn {z_1} là đường tròn tâm I\left( { - 5;0} ight);R = 5

    Cũng theo giả thiết, ta có:

    \begin{matrix} \left| {{z_2} + 1 - 3i} ight| = \left| {{z_2} - 3 - 6i} ight| \hfill \\ \Leftrightarrow {\left( {{a_2} + 1} ight)^2} + {\left( {{b_2} - 3} ight)^2} = {\left( {{a_2} - 3} ight)^2} + {\left( {{b_2} - 6} ight)^2} \hfill \\ \Rightarrow 8{a_2} + 6{b_2} - 35 = 0. \hfill \\ \end{matrix}

    Tập hợp điểm biểu diễn {z_2} là đường thẳng \Delta :\,\,8x + 6y - 35 = 0

    d(I,\Delta ) = \frac{{\left| { - 5.8 - 35} ight|}}{{\sqrt {{8^2} + {6^2}} }} = \frac{{15}}{2} \Rightarrow d\left( {I,\Delta } ight) > R

    \Rightarrow \min \left| {{z_1} - {z_2}} ight| = d\left( {I,\Delta } ight) - R = \frac{5}{2}

  • Câu 10: Thông hiểu
    Tính giá trị x và y thỏa mãn điều kiện

    Cho {\left( {x + 2i} ight)^2} = 3x + yi,\left( {x,y \in \mathbb{R}} ight). Giá trị của x và y bằng:

    Hướng dẫn:

     Ta có:

    {\left( {x + 2i} ight)^2} = 3x + yi \Leftrightarrow {x^2} - 4 + 4xi = 3x + yi

    \Leftrightarrow \left\{ \begin{gathered} {x^2} - 4 = 3x \hfill \\ 4x = y \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} x = - 1 \hfill \\ x = 4 \hfill \\ \end{gathered} ight. \hfill \\ 4x = y \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x = - 1 \hfill \\ y = - 4 \hfill \\ \end{gathered} ight. \hfill \\ \left\{ \begin{gathered} x = 4 \hfill \\ y = 16 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight.

  • Câu 11: Vận dụng cao
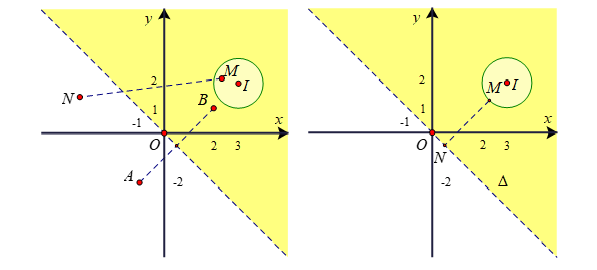
    Tìm giá trị nhỏ nhất của P

    Cho hai số phức z, w thỏa mãn \left\{ \begin{gathered} \left| {z - 3 - 2i} ight| \leqslant 1 \hfill \\ \left| {w + 1 + 2i} ight| \leqslant \left| {w - 2 - i} ight| \hfill \\ \end{gathered} ight.. Tìm giá trị nhỏ nhất của biểu thức P = \left| {z - w} ight|

    Hướng dẫn:

     Cách 1 :

    Giả sử z = a + bi,\left( {a,b \in \mathbb{R}} ight);w = x + yi,\left( {x,y \in \mathbb{R}} ight)

    \left| {z - 3 - 2i} ight| \leqslant 1 \Leftrightarrow {\left( {a - 3} ight)^2} + {\left( {b - 2} ight)^2} \leqslant 1(1)

    \left| {w + 1 + 2i} ight| \leqslant \left| {w - 2 - i} ight| \Leftrightarrow {\left( {x + 1} ight)^2} + {\left( {y + 2} ight)^2} \leqslant {\left( {x - 2} ight)^2} + {\left( {y - 1} ight)^2}

    Suy ra x + y = 0

    P = \left| {z - w} ight| = \sqrt {{{\left( {a - x} ight)}^2} + {{\left( {b - y} ight)}^2}} = \sqrt {{{\left( {a - x} ight)}^2} + {{\left( {b + x} ight)}^2}}

    Từ (1) ta có I(3; 2), bán kính r = 1. Gọi H là hình chiếu của I trên d:y = - x.

    Đường thẳng HI có PTTS: \left\{ \begin{gathered} x = 3 + t \hfill \\ y = 2 + t \hfill \\ \end{gathered} ight.

    \begin{matrix} M \in HI \Rightarrow M\left( {3 + t;\,2 + t} ight) \hfill \\ M \in \left( C ight) \Leftrightarrow 2{t^2} = 1 \Leftrightarrow \left[ \begin{gathered} t = \dfrac{1}{{\sqrt 2 }} \hfill \\ t = - \dfrac{1}{{\sqrt 2 }} \hfill \\ \end{gathered} ight. \hfill \\ t = 2 \Rightarrow M\left( {3 + \dfrac{1}{{\sqrt 2 }};\,2 + \dfrac{1}{{\sqrt 2 }}} ight),MH = \dfrac{{5 + \sqrt 2 }}{{\sqrt 2 }} \hfill \\ t = 3 \Rightarrow M\left( {3 - \dfrac{1}{{\sqrt 2 }};\,2 - \dfrac{1}{{\sqrt 2 }}} ight),MH = \dfrac{{5 - \sqrt 2 }}{{\sqrt 2 }} \hfill \\ \end{matrix}

    Vậy {P_{\min }} = \frac{{5\sqrt 2 - 2}}{2}

    Cách 2 :

    \left| {z - 3 - 2i} ight| \leqslant 1 điều này cho thấy M(z) đang nằm trên hình tròn tâm I(3; 2) bán kính bằng 1.

    \left| {w + 1 + 2i} ight| \leqslant \left| {w - 2 - i} ight| điều này cho thấy N(w) đang thuộc nửa mặt phẳng tạo bởi đường thẳng \Delta là trung trực của đoạn AB với A\left( { - 1; - 2} ight),B\left( {2;1} ight).

    \Delta :x + y = 0.

    (Minh hoạ như hình vẽ)

    Tìm giá trị nhỏ nhất của P

    P = \left| {z - w} ight| = MN.

    {P_{\min }} = d\left( {I,\Delta } ight) - R = \frac{{\left| {3 + 2} ight|}}{{\sqrt 2 }} - 1 = \frac{{5\sqrt 2 - 2}}{2}.

  • Câu 12: Vận dụng
    Tìm số phức z thỏa mãn điều kiện

    Cho z1 = 1 + i; z2 = -1 - i. Tìm {z_3} \in \mathbb{C} sao cho các điểm biểu diễn của {z_1};\,\,{z_2};\,\,{z_3} tạo thành tam giác đều.

    Hướng dẫn:

     Giả sử {z_3} = x + yi

    Để các điểm biểu diễn của {z_1};\,\,{z_2};\,\,{z_3} tạo thành một tam giác đều thì

    \left\{ {\begin{array}{*{20}{c}} {\left| {{z_1} - {z_2}} ight| = \left| {{z_1} - {z_3}} ight|} \\ {\left| {{z_1} - {z_2}} ight| = \left| {{z_2} - {z_3}} ight|} \end{array}} ight.

    \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\sqrt {4 + 4} = \sqrt {{{\left( {x - 1} ight)}^2} + {{\left( {y - 1} ight)}^2}} } \\ {\sqrt {4 + 4} = \sqrt {{{\left( {x + 1} ight)}^2} + {{\left( {y + 1} ight)}^2}} } \end{array}} ight.

    \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{{\left( {x - 1} ight)}^2} + {{\left( {y - 1} ight)}^2} = 8} \\ {x + y = 0} \end{array}} ight.

    \Rightarrow 2{y^2} = 6 \Rightarrow y = \pm \sqrt 3 \Rightarrow x = \mp \sqrt 3

    Vậy có hai số phức thoả mãn là: {z_3} = {\text{\{ }}\sqrt 3 - \sqrt 3 i;\,\, - \sqrt 3 + \sqrt 3 i\}

  • Câu 13: Vận dụng cao
    Tìm dạng đại số của w

    Cho {z_1} = 1 + \sqrt 3 i; {z_2} = \frac{{7 + i}}{{4 - 3i}}; {z_3} = {\left( {1 - i} ight)^{2016}}. Tìm dạng đại số của w = z_1^{25}.z_2^{10}.z_3^{2016}.

    Hướng dẫn:

     Ta có:

    \left. \begin{array}{l}z_1^{25} = {(1 + \sqrt 3 i)^{25}} = {8^8} + {8^8}\sqrt 3 i\\z_2^{10} = {\left( {\frac{{7 + i}}{{4 - 3i}}} ight)^{10}} = {(2i)^5} = {2^5}i\\z_3^{2016} = {(1 - i)^{2016}} = {( - 2i)^{1008}} = {2^{1008}}\end{array} ight\}

    \Rightarrow w = z_1^{25}.z_2^{10}.z_3^{2016} = - {2^{1037}}\sqrt 3 + {2^{1037}}i.

  • Câu 14: Vận dụng cao
    Tính môđun của số phức Z

    Tính môđun của số phức z thỏa mãn 3z.\overline z + 2023(z + \overline z ) = 48 - 2022i

    Hướng dẫn:

     - Đặt z = a + bi{\text{ }}(a,b \in \mathbb{R}); \Rightarrow \overline z = a - b

    - Ta có: 3z.\overline z + 2023(z + \overline z ) = 48 - 2022i

    \Leftrightarrow 3({a^2} + {b^2}) + 4046b.i = 48 - 2022i \Rightarrow {a^2} + {b^2} = 16

    - Vậy \left| z ight| = \sqrt {{a^2} + {b^2}} = 4

  • Câu 15: Vận dụng
    Chọn khẳng định trong các khẳng định dưới đây

    Cho số phức z thỏa mãn \left| {z - 1 + i} ight| = 2. Chọn phát biểu đúng:

    Hướng dẫn:

     Giả sử: z = x + yi{\text{ }}\left( {x,y \in \mathbb{R}} ight)

    Theo bài ra ta có:

    \left| {z - 1 + i} ight| = 2

    \Leftrightarrow \left| {\left( {x - 1} ight) + \left( {y + 1} ight)i} ight| = 2

    \Leftrightarrow {\left( {x - 1} ight)^2} + {\left( {y + 1} ight)^2} = 4

  • Câu 16: Thông hiểu
    Tính giá trị

    Cho phương trình {z^2} - 2z + 3 = 0 có hai nghiệm {z_1},{z_2} là . Giá trị của w = z_1^2 + z_2^2 + {z_1}{z_2} là?

    1 || Một || một

    Đáp án là:

    Cho phương trình {z^2} - 2z + 3 = 0 có hai nghiệm {z_1},{z_2} là . Giá trị của w = z_1^2 + z_2^2 + {z_1}{z_2} là?

    1 || Một || một

    Ta có:

    {z^2} - 2z + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}z = 1 + \sqrt 2 i\\z = 1 - \sqrt 2 i\end{array} ight.

    Suy ra:  w = z_1^2 + z_2^2 + {z_1}{z_2}

    = {\left( {1 + \sqrt 2 i} ight)^2} + {\left( {1 - \sqrt 2 i} ight)^2} + \left( {1 + \sqrt 2 i} ight)\left( {1 - \sqrt 2 i} ight) = 1

  • Câu 17: Vận dụng cao
    Tìm phần ảo

    Biết {z_1},{z_2} = 5 - 4i và {z_3} là ba nghiệm của phương trình {z^3} + b{z^2} + cz + d = 0\,\,\,\left( {b,c,d \in \mathbb R} ight),

    trong đó {z_3} là nghiệm có phần ảo dương. Phần ảo của số phức w = {z_1} + 3{z_2} + 2\,{z_3} bằng:

    Hướng dẫn:

     Xét phương trình {z^3} + b{z^2} + cz + d = 0\,\,\,\left( {b,c,d \in \mathbb R} ight) là phương trình bậc ba với hệ số thực nên luôn có một nghiệm thực là z_1.

    Do đó phương trình tương đương với:

    \left( {z - {z_1}} ight)\left( {{z^2} + a'z + b'} ight) = 0\,\,\,\left( {a',b' \in \mathbb R} ight)

    \Leftrightarrow \left[ \begin{array}{l}z = {z_1}\,\, \in \mathbb R\\{z^2} + a'z + b' = 0\,\,\,\left( 1 ight)\end{array} ight..

    Nên {z_3},{z_2} = 5 - 4i là hai nghiệm phức của phương trình bậc hai với hệ số thực (1).

    Suy ra .{z_3} = 5 + 4i

    Khi đó : w = {z_1} + 3{z_2} + 2\,{z_3} = {z_1} + 3.\left( {5 - 4i} ight) + 2.\left( {5 + 4i} ight) = \left( {25 + 2{z_3}} ight) - 4i.

    Vậy phần ảo của w = {z_1} + 3{z_2} + 2\,{z_3} là -4.

  • Câu 18: Vận dụng
    Chọn phương án đúng nhất

    Cho hai điểm A, B là hai điểm biểu diễn hình học số phức theo thứ tự z_0, z_1, khác 0 và

    thỏa mãn đẳng thức z_0^2+z_1^2=z_0z_1. Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ) ? Chọn phương án đúng và đầy đủ nhất.

    Hướng dẫn:

    Hai điểm A, B là hai điểm biểu diễn hình học số phức theo thứ tự z_0, z_1.

    Theo giả thiết suy ra: OA=|z_0|, OB=|z_1| và AB=|z_1-z_0|.

    Ta có: z_0^2+z_1^2=z_0z_1 \Leftrightarrow z_0^2-z_0z_1+z_1^2=0.

    \Leftrightarrow (z_0 +z_1)(z_0^2-z_0z_1+z_1^2)=0

    \Leftrightarrow z_0^3+z_1^3=0 \Leftrightarrow z_0^3=-z_1^2\Leftrightarrow |z_0|=|z_1| \Leftrightarrow OA=OB

    Xét (z_1-z_0)^2=z_0^2+z_1^2-2z_0z_1=-z_0z_1 \Rightarrow |z_1-z_0|^2=|z_1|.|z_0|

    \Leftrightarrow AB^2=OA.OB \Leftrightarrow AB=OB.

    Vậy OA=OB=AB hay tam giác OAB là tam giác đều.

  • Câu 19: Nhận biết
    Tìm số phức?

    Cho số phức z = {\left( {2i} ight)^4} - \frac{{{{\left( {1 + i} ight)}^6}}}{{5i}}. Số phức \overline {5z + 3i} là số phức nào sau đây?

    Hướng dẫn:

     Ta tính được z = \frac{{88}}{5} \Rightarrow 5z + 3i = 88 + 3i

  • Câu 20: Thông hiểu
    Tìm phần ảo của số phức

    Cho số phức z = a + bi. Số phức {z^2} có phần ảo là:

    Hướng dẫn:

    Ta có: {z^2} = {\left( {a + bi} ight)^2} = {a^2} - {b^2} + 2abi

  • Câu 21: Vận dụng cao
    Tìm GTLN của môđun số phức z

    Cho số phức z = \frac{{ - m + i}}{{1 - m(m - 2i)}},\,\,m \in \mathbb R. Tìm {\left| z ight|_{\max }}?

    Hướng dẫn:

     Ta có: z = \frac{{ - m + i}}{{1 - m(m - 2i)}} = \frac{m}{{{m^2} + 1}} + \frac{i}{{{m^2} + 1}}

    \Rightarrow \left| z ight| = \sqrt {\frac{1}{{{m^2} + 1}}} \le 1

    \Rightarrow {\left| z ight|_{\max }} = 1 \Leftrightarrow m = 0.

  • Câu 22: Vận dụng cao
    Tính giá trị nhỏ nhất của mođun số phức

    Cho hai số phức {z_1},{z_2} thỏa mãn \left| {{z_1} + 1 - i} ight| = 2 và {z_2} = i{z_1}.

    Tìm giá trị nhỏ nhất m của biểu thức \left| {{z_1} - {z_2}} ight|?

    Hướng dẫn:

    Vì \left| {{z_1} + 1 - i} ight| = 2 nên điểm biểu diễn {M_1} của {z_1} thuộc đường tròn tâm I(-1; 1) bán kính R = 2

    Vì {z_2} = i{z_1} nên điểm {M_2} (điểm biểu diễn của {z_2}) là ảnh của {M_1} qua phép quay tâm O, góc quay {90^0}

    => \left| {{z_1} - {z_2}} ight| = {M_1}{M_2} = \sqrt 2 O{M_1} ngắn nhất khi O{M_1} ngắn nhất

    Ta có: \min O{M_1} = R - OI = 2 - \sqrt 2

    Vậy: m = \sqrt 2 \left( {2 - \sqrt 2 } ight) = 2\sqrt 2 - 2

    Do \left| {{z_1} + 1 - i} ight| = 2 nên điểm biểu diễn của thuộc đường tròn tâm I\left( { - 1;1} ight) bán kính R  = 2.

    \left| {{z_1} - {z_2}} ight| = \left| {{z_1} - i{z_1}} ight| = \left| {\left( {1 - i} ight){z_1}} ight| = \sqrt 2 \left| {{z_1}} ight| = \sqrt 2 OM \geqslant \sqrt 2 \left( {R - OI} ight) = \sqrt 2 \left( {2 - \sqrt 2 } ight) = 2\sqrt 2 - 2

  • Câu 23: Vận dụng
    Biểu diễn số phức z

    Điểm biểu diễn của số phức z = \frac{1}{{2 - 3i}} là:

    Hướng dẫn:

     Ta có: z = \frac{1}{{2 - 3i}} = \frac{2}{{13}} + \frac{3}{{13}}i

  • Câu 24: Nhận biết
    Số phức liên hợp của số phức

    Số phức liên hợp của số phức 5 - 3i là

    Gợi ý:

     Cho số phức z = a + bi. Số phức \overline z = a – bi gọi là số phức liên hợp với số phức trên hay \overline z = \overline {a + bi} = a - bi

    Hướng dẫn:

    \overline z = \overline {a + bi} = a – bi

    \Rightarrow \overline z = \overline {5 - 3i} = 5 - ( - 3i) = 5 + 3i

  • Câu 25: Nhận biết
    Tính giá trị biểu thức

    Giá trị của z = 1 + i + {i^2} + ... + {i^{2023}} là?

    Hướng dẫn:

    Ta có: z = \frac{{{i^{2022}} - 1}}{{i - 1}} = 1 + i

    (Áp dụng công thức: {S_n} = 1 + p + {p^2} + ... + {p^n} = \frac{{{p^{n - 1}} - 1}}{{p - 1}})

  • Câu 26: Vận dụng
    Tìm tổng các giá trị

    Tìm tổng các giá trị của số thực a sao cho phương trình {z^2} + 3z + {a^2} - 2a = 0 có nghiệm phức z_0 thỏa mãn \left| {{z_{m{o}}}} ight| = 2. 

    4 || Bốn || bốn

    Đáp án là:

    Tìm tổng các giá trị của số thực a sao cho phương trình {z^2} + 3z + {a^2} - 2a = 0 có nghiệm phức z_0 thỏa mãn \left| {{z_{m{o}}}} ight| = 2. 

    4 || Bốn || bốn

     Ta có với mọi a \in \mathbb R thì phương trình {z^2} + 3z + {a^2} - 2a = 0 luôn có nghiệm phức.

    {z_1} = \frac{{ - 3 + i\sqrt {\left| { - 4{a^2} + 8a + 9} ight|} }}{2} và {z_2} = \frac{{ - 3 - i\sqrt {\left| { - 4{a^2} + 8a + 9} ight|} }}{2}.

    Suy ra \left| {{z_1}} ight| = \left| {{z_2}} ight| = \sqrt {\frac{3}{4} + \frac{{\left| { - 4{a^2} + 8a + 9} ight|}}{4}}.

     

    \left| {{z_{m{o}}}} ight| = 2 \Rightarrow \sqrt {\frac{3}{4} + \frac{{\left| { - 4{a^2} + 8a + 9} ight|}}{4}} = 2

    \Leftrightarrow \frac{9}{4} + \frac{{\left| { - 4{a^2} + 8a + 9} ight|}}{4} = 4 \Leftrightarrow \left| { - 4{a^2} + 8a + 9} ight| = 7

    \Leftrightarrow \left[ \begin{array}{l} - 4{a^2} + 8a + 9 = 7\\ - 4{a^2} + 8a + 9 = - 7\end{array} ight. \Leftrightarrow \left[ \begin{array}{l} - 4{a^2} + 8a + 2 = 0{m{ }}\left( 1 ight)\\ - 4{a^2} + 8a + 16 = 0{m{ }}\left( 2 ight)\end{array} ight.

    Từ (1) ta có  {a_1} + {a_2} = 2, từ (2) ta có {a_3} + {a_4} = 2.

    Vậy tổng {a_1} + {a_2} + {a_3} + {a_4} = 4.

  • Câu 27: Nhận biết
    Nghiệm của PT bậc 3

    Phương trình {z^3} + 4{z^2} + (4 + i)z + 3 + 3i = 0 có tập nghiệm là:

    Hướng dẫn:

    Dễ thấy z=-i  là nghiệm của {z^3} + 4{z^2} + (4 + i)z + 3 + 3i = 0

    Nên {z^3} + 4{z^2} + (4 + i)z + 3 + 3i = 0 \Leftrightarrow \,(z + i)({z^2} + (4 - i)z + 3 - 3i) = 0

    \Leftrightarrow \left[ \begin{array}{l}z + i = 0\\{z^2} + (4 - i)z + 3 - 3i = 0\,\,\,(*)\end{array} ight.

    Giải (*), ta được:

    \Delta = {(4 - i)^2} - 12 + 12i = 16 - 1 - 8i - 12 + 12i

    = 3 + 4i = 4 + 2.2.i + {i^2} = {(2 + i)^2}

    Vậy có hai căn bậc hai là: 2+i và -2-i

    Do đó nghiệm của pt là \left[ \begin{array}{l}z = \dfrac{{ - 4 + i + 2 + i}}{2} = - 1 + i\\z = \dfrac{{ - 4 + i - 2 - i - 2}}{2} = - 3\end{array} ight.

    Vậy PT có 3 nghiệm là –i, -3, -1+i.

  • Câu 28: Thông hiểu
    Khẳng định đúng?

    Số phức z thỏa mãn z = 1 + 2i + 3{i^2} + 4{i^3} + ... + 18{i^{19}}. Khẳng định nào sau đây là khẳng định đúng?

    Hướng dẫn:

    Ta có:  z - iz = 1 + i + ... + {i^{19}} - 18{i^{20}} = 1.\frac{{1 - {i^{20}}}}{{1 - i}} - 18{i^{20}} = - 18

    \Rightarrow z = \frac{{ - 18}}{{1 - i}} = - 9 - 9i

  • Câu 29: Thông hiểu
    Phần thực của số phức z là?

    Cho số phức z = 1 + \left( {1 + i} ight) + {\left( {1 + i} ight)^2} + ... + {\left( {1 + i} ight)^{26}}. Phần thực của số phức z là?

    Hướng dẫn:

     Ta có: z = 1 + \left( {1 + i} ight) + {\left( {1 + i} ight)^2} + ... + {\left( {1 + i} ight)^{26}} = \frac{{{{\left( {1 + i} ight)}^{27}} - 1}}{i}

    = \frac{{{{\left( {1 + i} ight)}^{26}}.\left( {1 + i} ight) - 1}}{i} = \frac{{{{(2i)}^{13}}\left( {1 + i} ight) - 1}}{i}

    = \frac{{{2^{13}}i - {2^{13}} - 1}}{i} = {2^{13}} + (1 + {2^{13}})i

    Vậy phần thực là  2^{13}.

  • Câu 30: Thông hiểu
    Điểm biểu diễn của số phức

    Kí hiệu z_0 là nghiệm phức có phần ảo dương của phương trình 4{z^2} - 16z + 17 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w = i{z_0}?

    Hướng dẫn:

     Ta có:

    4{z^2} - 16z + 17 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_0} = 2 + \dfrac{1}{2}i\\z = 2 - \dfrac{1}{2}i\end{array} ight.

    \Rightarrow w = i{z_0} = - \frac{1}{2} + 2i

0/30
30 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (23%):
    2/3
  • Thông hiểu (27%):
    2/3
  • Vận dụng (20%):
    2/3
  • Vận dụng cao (30%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 4 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập