Lớp 12 Toán 12

Luyện tập Ứng dụng của tích phân (Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Tính thể tích của vật

    Thiết diện của vật thể cắt bởi mặt phẳng \left( P ight) vuông góc với trục Ox tại điểm có hoành độ x;\left( {0 \leqslant x \leqslant 1} ight) là một hình chữ nhật có độ dài hai cạnh x và \ln \left( {{x^2} + 1} ight). Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x=1.

    Hướng dẫn:

    Do thiết diện là hình chữ nhật nên diện tích của thiết diện là  S\left( x ight) = x.\ln \left( {{x^2} + 1} ight)

    Ta có thể tích cần tính là:

    \begin{matrix} V = \int\limits_0^1 {x\ln \left( {{x^2} + 1} ight)dx} = \dfrac{1}{2}\int\limits_0^1 {\ln \left( {{x^2} + 1} ight)d\left( {{x^2} + 1} ight)} \hfill \\ = \left. {\frac{1}{2}.\left( {{x^2} + 1} ight)\ln \left( {{x^2} + 1} ight)} ight|_0^1 - \dfrac{1}{2}\int\limits_0^1 {\left( {{x^2} + 1} ight)d\left( {\ln \left( {{x^2} + 1} ight)} ight)} \hfill \\ = \ln 2 - \frac{1}{2}\int\limits_0^1 {2xd\left( x ight) = \ln 2 - \dfrac{1}{2}} \hfill \\ \end{matrix}

  • Câu 2: Thông hiểu
    Tính diện tích hình phẳng

    Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x ight) = \frac{{ - x - 2}}{{x - 1}}, trục hoành và các đường thẳng x = - 1;x = 0

    Hướng dẫn:

     Gọi S là diện tích của hình phẳng trên ta có: S = \int\limits_{ - 1}^0 {\left| {\frac{{ - x - 2}}{{x - 1}}} ight|dx}

    Ta có: \frac{{ - x - 2}}{{x - 1}} \geqslant 0;\forall x \in \left[ { - 1;0} ight]

    Khi đó:

    \begin{matrix} S = \int\limits_{ - 1}^0 {\left| {\dfrac{{ - x - 2}}{{x - 1}}} ight|dx} = \int\limits_{ - 1}^0 {\left( {\dfrac{{ - x - 2}}{{x - 1}}} ight)dx} \hfill \\ = \int\limits_{ - 1}^0 {\dfrac{{ - \left( {x - 1} ight) - 3}}{{x - 1}}dx} = \int\limits_{ - 1}^0 {\left( { - 1 - \dfrac{3}{{x - 1}}} ight)dx} \hfill \\ = \left. {\left( { - x - 3\ln \left| {x - 1} ight|} ight)} ight|_{ - 1}^0 = 3\ln 2 - 1 \hfill \\ \end{matrix}

  • Câu 3: Vận dụng
    Tính diện tích hình phẳng

    Tính diện tích hình phẳng giới hạn bởi y = \left| {2{x^2} - 4x} ight|;y = x + 3

    Hướng dẫn:

     Xét phương trình hoành độ giao điểm ta có:

    \begin{matrix} \left| {2{x^2} - 4x} ight| = x + 3 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{l}} {2{x^2} - 4x \geqslant 0} \\ {2{x^2} - 4x = x + 3} \end{array}} ight.} \\ {\left\{ {\begin{array}{*{20}{l}} {2{x^2} - 4x \leqslant 0} \\ { - \left( {2{x^2} - 4x} ight) = x + 3} \end{array}} ight.} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = - \dfrac{1}{2}} \\ {x = 3} \end{array}} ight. \hfill \\ \end{matrix}

    Diện tích hình phẳng cần tính là:

    \begin{matrix} S = \int_{ - \dfrac{1}{2}}^3 | |2{x^2} - 4x| - x - 3|{\text{d}}x \hfill \\ = \left| {\int_{ - \dfrac{1}{2}}^0 {\left( {2{x^2} - 5x - 3} ight)} {\text{d}}x} ight| + \left| {\int_0^2 {\left( { - 2{x^2} + 3x - 3} ight)} {\text{d}}x} ight| + \left| {\int_2^3 {\left( {2{x^2} - 5x - 3} ight)} {\text{d}}x} ight| \hfill \\ = \dfrac{{19}}{{24}} + \dfrac{{16}}{3} + \dfrac{{17}}{6} = \dfrac{{215}}{{24}}({\text{dvdt}}) \hfill \\ \end{matrix}

  • Câu 4: Thông hiểu
    Thể tích khối tròn xoay

    Thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường y = x\sqrt {\ln \left( {1 + {x^3}} ight)} ;y = 0;x = 1, khi xoay quanh trục Ox.

    Hướng dẫn:

     Phương trình hoành độ giao điểm là: x\sqrt {\ln \left( {1 + {x^3}} ight)} = 0 \Leftrightarrow x = 0

    Gọi là thể tích khối tròn xoay cần tìm ta có: V= \pi \int\limits_0^1 {{x^2}\ln \left( {1 + {x^3}} ight)dx}

    Đặt \left\{ {\begin{array}{*{20}{c}} {u = \ln \left( {1 + {x^3}} ight)} \\ {dv = {x^2}dx} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {du = \dfrac{{3{x^2}}}{{1 + {x^3}}}dx} \\ {v = \dfrac{{{x^3} + 1}}{3}} \end{array}} ight.

    \begin{matrix} \Rightarrow V = \pi \left\{ {\left[ {\dfrac{{{x^3} + 1}}{3}\ln \left( {1 + {x^3}} ight)} ight]_0^1 - \int\limits_0^1 {{x^2}dx} } ight\} \hfill \\ \Rightarrow V = \pi \left( {\dfrac{{2\ln 2}}{3} - \dfrac{1}{3}} ight) \hfill \\ \end{matrix}

  • Câu 5: Vận dụng
    Hoành độ điểm A thuộc khoảng nào dưới đây?

    Cho đường cong (C) y = {x^3}. Xét điểm A có hoành độ dương thuộc (C), tiếp tuyến của (C) tại A tạo với (C) một hình phẳng có diện tích bằng 27. Hoành độ điểm A thuộc khoảng nào dưới đây?

    Hướng dẫn:

    Ta có: y' = 3{x^2}

    Ta có: A \in \left( C ight) \Rightarrow A\left( {a;{a^3}} ight);a > 0

    Phương trình tiếp tuyến d của (C) tại A là d:y = 3{a^2}\left( {x - a} ight) + {a^3}

    Ta có phương trình hoành độ giao điểm d và (C) là:

    \begin{matrix} {x^3} = 3{a^2}\left( {x - a} ight) + {a^3} \hfill \\ \Leftrightarrow {\left( {x - a} ight)^2}\left( {x + 2a} ight) = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = a} \\ {x = - 2a} \end{array}} ight. \hfill \\ \end{matrix}

    Gọi S là diện tích của hình phẳng giới hạn bởi tiếp tuyến d và (C).

    Ta có:

    \begin{matrix} S = 27 \hfill \\ \Rightarrow \int\limits_{ - 2a}^a {\left| {{x^3} - 3{a^2}\left( {x - a} ight) - {a^3}} ight|dx = 27} \hfill \\ \Rightarrow \left| {\int\limits_{ - 2a}^a {\left( {{x^3} - 3{a^2}\left( {x - a} ight) - {a^3}} ight)dx} } ight| = 27 \hfill \\ \Rightarrow \left| {\left. {\left( {\dfrac{{{x^4}}}{4} - \dfrac{{3{a^2}{x^2}}}{2} + 2{a^3}x} ight)} ight|_{ - 2a}^a} ight| = 27 \hfill \\ \Leftrightarrow \dfrac{{27}}{4}{a^4} = 27 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {a = \sqrt 2 \left( {tm} ight)} \\ {a = - \sqrt 2 \left( {ktm} ight)} \end{array}} ight. \Rightarrow a = \sqrt 2 \hfill \\ \end{matrix}

  • Câu 6: Vận dụng
    Tìm vận tốc của chất điểm B

    Một chất điểm A từ trạng thái nghỉ chuyển động với vận tốc nhanh dần đều, 8 giây sau nó đạt đến vận tốc 6m/s. Từ thời điểm đó nó chuyển động đều. Một chất điểm B khác xuất phát từ cùng vị trí A nhưng chậm hơn nó 12 giây với vận tốc nhanh dần đều và đuổi kịp A sau 8 giây (kể từ lúc B xuất phát). Tìm vận tốc B tại thời điểm đó.

    Hướng dẫn:

    Phương trình vận tốc của vật A là {v_1} = a.t

    Ta có: v\left( 8 ight) = 6 \Rightarrow a = \frac{3}{4} \Rightarrow {v_1} = \frac{3}{4}t

    Quãng đường vật A đi được sau 20s đầu là: \int\limits_0^8 {\frac{3}{4}tdt + 6.12 = 96\left( m ight)}

    Phương trình vận tốc của vật B là

    \begin{matrix} {v_2} = bt \Rightarrow {S_B} = \int\limits_0^8 {btdt} = 96 \Rightarrow b = 3 \hfill \\ \Rightarrow {v_2} = bt \hfill \\ \end{matrix}

    => Vận tốc của vật B khi hai vật gặp nhau là: {v_B} = 3.8 = 24\left( {m/s} ight)

  • Câu 7: Nhận biết
    Tính thể tích V

    Cho hình phẳng D giới hạn bởi đường cong y = \sqrt {2 + \cos x}, trục hoành và các đường thẳng x = 0;x = \frac{\pi }{2}. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V là:

    Hướng dẫn:

    Thể tích cần tính là:

    \begin{matrix} V = \pi \int\limits_0^{\frac{\pi }{2}} {{{\left( {\sqrt {2 + \cos x} } ight)}^2}dx} \hfill \\ \Rightarrow V = \pi \int\limits_0^{\frac{\pi }{2}} {\left( {2 + \cos x} ight)dx} \hfill \\ \Rightarrow V = \left. {\pi \left( {2 + \sin x} ight)} ight|_0^{\frac{\pi }{2}} = \pi \left( {\pi + 1} ight) \hfill \\ \end{matrix}

     

  • Câu 8: Vận dụng
    Tìm tỉ số diện tích

    Cho đường tròn \left( C ight):{x^2} + {y^2} = 8 và parabol \left( P ight):{y^2} = 2x. \left( P ight) cắt \left( C ight) thành hai phần. Tìm tỉ số diện tích của hai phần đó.

    Hướng dẫn:

    Hoành độ giao điểm của (P) và (C) là: 2x = 8 - {x^2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 2} \\ {x = - 4\left( L ight)} \end{array}} ight.

    Xét giao điểm thuộc góc phần tư thứ nhất, với x = 2 \Rightarrow y = 2

    Gọi S2 là phần có diện tích nhỏ hơn, S1 là phần còn lại

    Ta có:

    \begin{matrix} {S_2} = 2\int\limits_0^2 {\left[ {\sqrt {8 - {y^2}} - \dfrac{{{y^2}}}{2}} ight]} dy \hfill \\ = 2\int\limits_0^2 {\sqrt {8 - {y^2}} } dy - \int\limits_0^2 {{y^2}} dy \hfill \\ = 2I - \left. {\dfrac{{{y^3}}}{3}} ight|_0^2 = 2I - \dfrac{8}{3} \hfill \\ \end{matrix}

    Đặt y = 2\sqrt 2 \sin t \Rightarrow dy = 2\sqrt 2 \cos tdt

    \begin{matrix} I = \int_0^2 {\sqrt {8 - {y^2}} } dy = \int_0^{\frac{\pi }{4}} {\sqrt {8 - 8{{\sin }^2}t} } .2\sqrt 2 \cos tdt \hfill \\ = 8\int_0^{\frac{\pi }{4}} {\sqrt {1 - {{\sin }^2}t} } .\cos tdt = 8\int_0^{\frac{\pi }{4}} {{{\cos }^2}} tdt \hfill \\ = 4\int_0^{\frac{\pi }{4}} {(1 + \cos 2t)} dt = \left. {4\left[ {t + \frac{1}{2}\sin 2t} ight]} ight|_0^{\frac{\pi }{4}} = \pi + 2 \hfill \\ \end{matrix}

    Khi đó {S_2} = 2\pi + \frac{4}{3}

    Diện tích hình tròn {S_2} = \pi {\left( {2\sqrt 2 } ight)^2} = 8\pi

    \begin{matrix} {S_1} = 8\pi - \left( {2\pi + \dfrac{4}{3}} ight) = 6\pi - \dfrac{4}{3} \hfill \\ \Rightarrow \dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{9\pi - 2}}{{3\pi + 2}} \hfill \\ \end{matrix}

  • Câu 9: Vận dụng
    Tính diện tích hình phẳng

    Tính diện tích hình phẳng được giới hạn bởi đồ thị \left( P ight): y= {x^2} - 1 và hai tiếp tuyến của \left( P ight) tại A\left( { - 1;0} ight);B\left( {2;3} ight)

    Hướng dẫn:

    Ta có hình vẽ minh họa như sau:

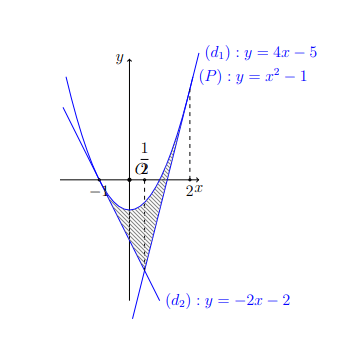
    Tính diện tích hình phẳng

    Phương trình tiếp tuyến của (P) tại A(-1;0) là: \left( {{d_2}} ight):y = - 2x - 2

    Phương trình tiếp tuyến của (P) tại B(2;3) là: \left( {{d_1}} ight):y = 4x - 5

    Từ hình vẽ ta suy ra diện tích của hình phẳng cần tìm là:

    \begin{matrix} S = \int_{ - 1}^{\frac{1}{2}} {\left( {{x^2} - 1 - ( - 2x - 2)} ight)} {\text{d}}x + \int_{\frac{1}{2}}^2 {\left( {{x^2} - 1 - (4x - 5)} ight)} {\text{d}}x \hfill \\ = \int_{ - 1}^{\frac{1}{2}} {\left( {{x^2} + 2x + 1} ight)} {\text{d}}x + \int_{\frac{1}{2}}^2 {\left( {{x^2} - 4x + 4} ight)} {\text{d}}x \hfill \\ = \left. {\left( {\frac{1}{3}{x^3} + {x^2} + x} ight)} ight|_{ - 1}^{\dfrac{1}{2}} + \left. {\left( {\dfrac{1}{3}{x^3} - 2{x^2} + 4x} ight)} ight|_{\frac{1}{2}}^2 = \frac{9}{4} \hfill \\ \end{matrix}

  • Câu 10: Thông hiểu
    Tính vận tốc của vật chuyển động

    Một vật chuyển động với vận tốc ban đầu là 4m/s và gia tốc a\left( t ight) = 3{t^2} + t\left( {m/s} ight). Hỏi sau khi chuyển động với gia tốc đó được 2 giây thì vận tốc của vật là bao nhiêu?

    Hướng dẫn:

    Ta có: v\left( t ight) = \int {a\left( t ight)dt} = \int {\left( {3{t^2} + t} ight)dt} = {t^3} + \frac{1}{2}{t^2} + C\left( {m/s} ight)

    Do khi bắt đầu tăng tốc {v_0} = 4m/s nên

    {v_{\left( {t = 0} ight)}} = 4 \Rightarrow C = 4 \Rightarrow v\left( t ight) = {t^3} + \frac{1}{2}{t^2} + 4

    Vận tốc của vật khi chuyển động với gia tốc đó được là

    v\left( 2 ight) = {2^3} + \frac{1}{2}{.2^2} + 4 = 14\left( {m/s} ight)

  • Câu 11: Nhận biết
    Tính thể tích V

    Cho (H) là hình phẳng giới hạn bởi đường cong \left( C ight):y = {x^2} + 4x và đường thẳng d:y = x. Tính thể tích V của vật thể tròn xoay do hình phẳng (H) quay quanh trục hoành.

    Hướng dẫn:

    Phương trình hoành độ giao điểm là: - {x^2} + 4x = x \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {x = 3} \end{array}} ight.

    Thể tích cần tính là:

    V = \pi \int\limits_0^3 {\left| {{{\left( {4x - {x^2}} ight)}^2} - {x^2}} ight|dx} = \frac{{108\pi }}{3}

  • Câu 12: Vận dụng
    Xác định thời điểm chất điểm di chuyển xa nhất

    Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia tốc phụ thuộc thời gian t\left( s ight) là a\left( t ight) = 2t - 7\left( {m/{s^2}} ight). Biết vận tốc ban đầu bằng 10m/s, hỏi trong 6 giây đầu tiên, thời điểm nào chất điểm ở xa nhất về phía bên phải?

    Hướng dẫn:

    Vận tốc của vật được tính theo công thức v\left( t ight) = 10 + {t^2} - 7t\left( {m/s} ight)

    => Quãng đường vật di chuyển được tính theo công thức:

    S\left( t ight) = \int {v\left( t ight)dt} = \frac{{{t^3}}}{3} - \frac{{7t}}{2} + 10t\left( m ight)

    Ta có:

    \begin{matrix} S'\left( t ight) = {t^2} - 7t + 10 \hfill \\ \Rightarrow S'\left( t ight) = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}} {t = 0} \\ {t = 5} \end{array}} ight. \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {S\left( 0 ight) = 0} \\ {S\left( 2 ight) = \dfrac{{26}}{6}} \\ {S\left( 5 ight) = \dfrac{{25}}{6}} \\ {S\left( 6 ight) = 6} \end{array}} ight. \Rightarrow \mathop {MaxS\left( t ight)}\limits_{\left[ {0;6} ight]} = S\left( 2 ight) = \dfrac{{26}}{3} \hfill \\ \end{matrix}

  • Câu 13: Thông hiểu
    Thể tích V của khối tròn xoay

    Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bời các đường thẳng y = 0;y = x\sqrt {\ln \left( {x + 1} ight)} ;x = 1 xung quanh trục Ox là:

    Hướng dẫn:

    Phương trình hoành độ giao điểm của (C) và Ox là x\sqrt {\ln \left( {x + 1} ight)} = 0 \Rightarrow x = 0

    Thể tích khối tròn xoay cần tính là V = \pi \int\limits_0^1 {{x^2}\ln \left( {x + 1} ight)dx}

    Đặt \left\{ {\begin{array}{*{20}{c}} {u = \ln \left( {1 + x} ight)} \\ {dv = {x^2}dx} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {du = \dfrac{{dx}}{{x + 1}}} \\ {v = \dfrac{{{x^3} + 1}}{3}} \end{array}} ight.

    Ta có:

    \begin{matrix} V = \pi \int\limits_0^1 {{x^2}\ln \left( {x + 1} ight)dx} \hfill \\ = \pi \left\{ {\left. {\dfrac{{{x^3} + 1}}{3}\ln \left( {x + 1} ight)} ight|_0^1 - \int\limits_0^1 {\left( {{x^2} - x + 1} ight)dx} } ight\} \hfill \\ = \dfrac{{\pi \left( {12\ln 2 - 5} ight)}}{{18}} \hfill \\ \end{matrix}

  • Câu 14: Thông hiểu
    Tính diện tích S của hình phẳng

    Tính diện tích S của hình phẳng giới hạn bới đồ thị của hàm số y = {e^x} + x và các đường thẳng x - y + 1 = 0;x = \ln 5 là:

    Hướng dẫn:

     Ta có: x - y + 1 = 0 \Rightarrow y = x + 1

    Phương trình hoành độ giao điểm của hai đồ thị là

    {e^x} + x = x + 1 \Leftrightarrow {e^x} = 1 \Rightarrow x = 0

    Diện tích hình phẳng cần tìm là:

    \begin{matrix} S = \int\limits_0^{\ln 5} {\left| {{e^x} - 1} ight|dx} = \int\limits_0^{\ln 5} {\left( {{e^x} - 1} ight)dx} \hfill \\ = \left. {\left( {{e^x} - x} ight)} ight|_0^{\ln 5} = 4 - \ln 5 \hfill \\ \end{matrix}

  • Câu 15: Nhận biết
    Diện tích hình phẳng

    Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = {x^2} - x + 1;y = x + 1 là:

    Hướng dẫn:

    Phương trình hoành độ giao điểm 2 đồ thị là:

    {x^2} - x + = x + 1 \Leftrightarrow {x^2} - 2x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {z = 2} \end{array}} ight.

    Diện tích cần tìm là:

    \begin{matrix} S = \int\limits_0^2 {\left| {{x^2} - x + 1 - x - 1} ight|dx} = \int\limits_0^2 {\left| {{x^2} - 2x} ight|dx} \hfill \\ = \int\limits_0^2 {\left( {2x - {x^2}} ight)dx} = \left. {\left( {{x^2} - \dfrac{{{x^3}}}{3}} ight)} ight|_0^2 = \dfrac{4}{3} \hfill \\ \end{matrix}

  • Câu 16: Nhận biết
    Tính diện tích hình phẳng

    Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = - {x^2} + 2x - 2, trục hoành và các đường thẳng x = 0;x = 3

    Hướng dẫn:

    Diện tích S của hình phẳng trên là: S = \int\limits_0^3 {\left| { - {x^2} + 2x - 2} ight|dx}

    Ta có: - {x^2} + 2x - 2 \leqslant 0;\forall x \in \left[ {0;3} ight]

    => S = \int\limits_0^3 {\left| { - {x^2} + 2x - 2} ight|dx} = \int\limits_0^3 {\left( {{x^2} - 2x + 2} ight)dx = \left. {\left( {\frac{{{x^3}}}{3} - {x^2} + 2x} ight)} ight|_0^3 = 6\left( {dvdt} ight)}

  • Câu 17: Vận dụng
    Tính thể tích của một vật thể

    Tính thể tích của một vật thể nằm giữa hai mặt phẳng x = 0;x = \pi, biết thiết diện của vật thể cắt bởi mặt phẳng \left( P ight) vuông góc với trục Ox tại điểm có hoành độ  là một tam giác đều có cạnh bằng 2\sqrt {\sin x}

    Hướng dẫn:

     Diện tích thiết diện là S\left( x ight) = \frac{{{{\left( {2\sqrt {\sin x} } ight)}^2}.\sqrt 3 }}{4} = \sqrt 3 \sin x

    Ta có thể tích cần tính là V = \int\limits_0^\pi {\sqrt 3 \sin xdx = \left. { - \sqrt 3 \cos x} ight|_0^\pi = } 2\sqrt 3

  • Câu 18: Nhận biết
    Tính thể tích khối tròn xoay

    Cho hình phẳng \left( H ight) giới hạn với các đường y = {x^2};y = 0;x = 2. Tính thể tích V của khối tròn xoay thu được khi \left( H ight) quay quanh trục Ox?

    Hướng dẫn:

    Thể tích cần tìm là:

    V = \pi \int\limits_0^2 {{x^4}dx} = \left. {\pi .\frac{{{x^5}}}{5}} ight|_0^2 = \frac{{32\pi }}{5}

  • Câu 19: Thông hiểu
    Thể tích hình khối giới hạn bởi các đường thẳng quay quanh trục tung

    Thể tích hình khối do hình phẳng giới hạn bởi các đường thẳng x = {y^2} + 5;x = 3 - y quay quanh Oy.

    Hướng dẫn:

    Tung độ giao điểm 

    \begin{matrix} - {y^2} + 5 = 3 - y \Rightarrow \left[ {\begin{array}{*{20}{c}} {y = - 1} \\ {y = 2} \end{array}} ight. \hfill \\ \Rightarrow V = \pi \int\limits_{ - 1}^2 {\left| {{{\left( { - {y^2} + 5} ight)}^2} - {{\left( {3 - y} ight)}^2}} ight|dy = \dfrac{{153}}{5}\pi } \hfill \\ \end{matrix}

  • Câu 20: Nhận biết
    Tính thể tích khối tròn xoay

    Cho hình phẳng D giới hạn bới đường cong y = \sqrt {{x^2} + 1}, trục hoành và các đường thẳng x = 0;x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?

    Hướng dẫn:

    Thể tích cần tìm là: v = \pi \int\limits_0^1 {{{\left( {\sqrt {{x^2} + 1} } ight)}^2}dx} = \frac{{4\pi }}{3}

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (30%):
    2/3
  • Thông hiểu (30%):
    2/3
  • Vận dụng (40%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 19 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập